Diagrama de árvore

Este artigo explica o que é um diagrama de árvore e como ele é feito. Assim, você encontrará exemplos de estruturas em árvore, as vantagens deste tipo de diagrama e, além disso, um exercício resolvido passo a passo.

O que é uma árvore?

Um diagrama de árvore , também chamado de árvore de probabilidade , é uma representação gráfica de todos os resultados possíveis de um experimento junto com suas probabilidades.

Assim, um diagrama de árvore é usado para representar graficamente todos os resultados possíveis em um espaço amostral e calcular suas probabilidades.

Um diagrama de árvore é feito de tal forma que cada resultado ( nó ) se ramifica em novos resultados possíveis ( ramos ) até que os resultados finais sejam alcançados.

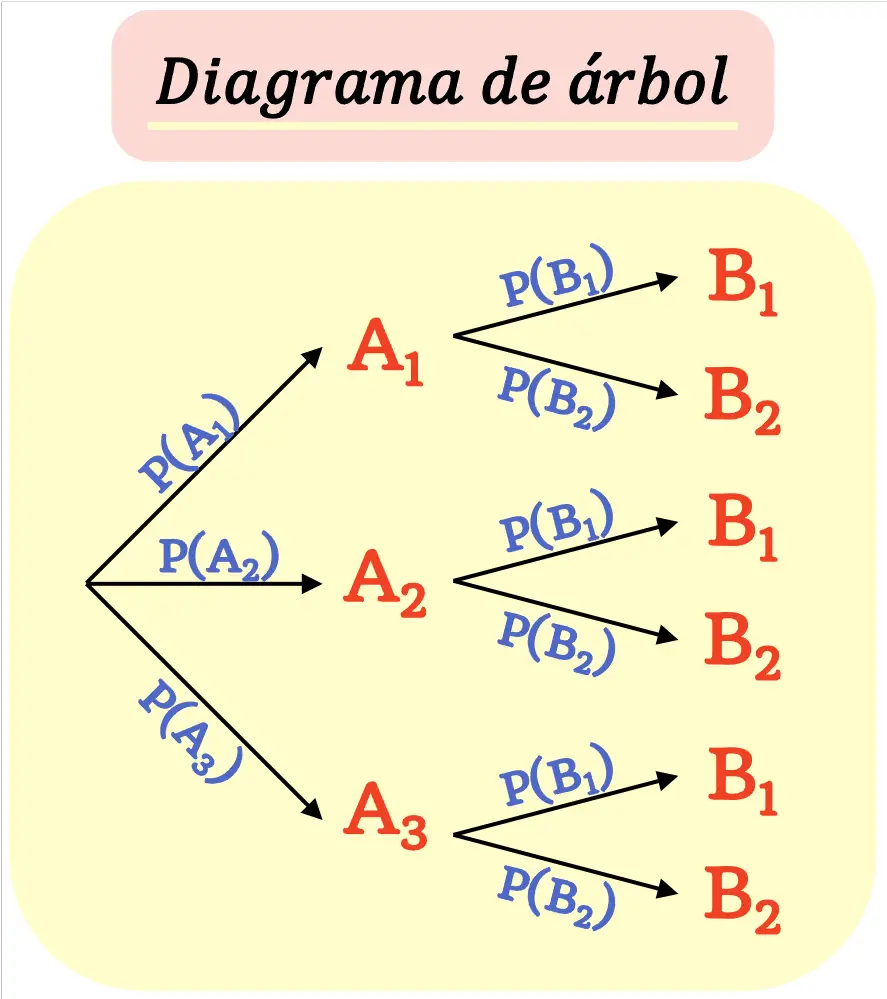
Deve-se ter em mente que a soma das probabilidades de todos os ramos que saem de um nó deve ser igual a 1.

Como fazer um diagrama de árvore

Para criar uma árvore, você deve seguir os seguintes passos:

1. O primeiro passo na criação de um diagrama de árvore é desenhar uma ramificação para cada resultado possível. Estes serão os ramos da primeira geração.
2. Então, a probabilidade associada a cada evento é adicionada ao seu ramo correspondente.
3. O final de cada ramo da primeira geração é um nó a partir do qual os ramos de possíveis eventos subsequentes devem ser representados.
4. Tal como nos primeiros ramos, devemos somar as probabilidades dos acontecimentos representados.
5. Repita as etapas 3 e 4 até chegar aos nós finais, ou seja, os possíveis finais do experimento.

Observe que o número de filiais em um nível não precisa necessariamente ser igual ao número de filiais em um nível diferente. Da mesma forma, o número de ramificações resultantes de um resultado possível pode variar até mesmo dentro do mesmo nível.

Exemplo de árvore

Agora que conhecemos a definição e a teoria da criação de um diagrama de árvore, vamos dar uma olhada passo a passo em um exemplo do mundo real para entender melhor o conceito.

• Construa a árvore de probabilidade do lançamento da moeda de três moedas independentes. Em seguida, determine a probabilidade de obter cara nos três lançamentos.

No sorteio, existem apenas dois resultados possíveis, podemos obter cara ou coroa. Portanto, a probabilidade de obter cara ou coroa no lançamento de uma moeda é:

Depois de conhecermos as probabilidades dos resultados possíveis, passamos a representar o diagrama de árvore.

Como os lançamentos de moedas são independentes, a probabilidade de obter cara ou coroa será sempre a mesma para cada lançamento. Portanto, para construir a árvore, dois galhos (cara e coroa) devem ser representados com a mesma probabilidade para cada lançamento realizado.

E uma vez que tenhamos feito a árvore, tudo o que precisamos fazer é determinar a probabilidade de conseguir o lançamento de três moedas.

Portanto, neste caso devemos multiplicar todas as probabilidades de obter cara, pois essas são as probabilidades do caminho que nos leva ao resultado desejado.

Assim, a probabilidade de obter cara nos três lançamentos de moeda é calculada da seguinte forma:

Resumindo, a probabilidade de obter cara três vezes seguidas é de 12,5%.

Exercício de árvore resolvido

Numa aldeia existem apenas 3 creches: 60% das crianças vão para a creche A, 30% para a creche B e 10% para a creche C. Além disso, nas três creches, 55% das pessoas são meninas. Construa a árvore e calcule as seguintes probabilidades:

• Probabilidade de que, quando uma criança é selecionada aleatoriamente, seja uma menina da creche B.
• Probabilidade de que, quando uma criança for selecionada aleatoriamente em qualquer creche, seja um menino.

Observe que se a proporção de meninas em todas as creches for de 55%, o percentual de meninos é calculado simplesmente subtraindo 1 menos 0,55:

Agora que conhecemos todas as probabilidades, podemos criar a árvore de probabilidades com todas as possibilidades:

Assim, a probabilidade de selecionar aleatoriamente uma menina da creche B é calculada da seguinte forma:

Por outro lado, para determinar a probabilidade de selecionar um menino em qualquer creche, devemos primeiro encontrar a probabilidade de selecionar um menino para cada creche e depois somá-las:

Vantagens da estrutura em árvore

Devido às características da estrutura em árvore, as vantagens deste tipo de gráfico estatístico são as seguintes:

• Os diagramas de árvore são muito úteis para a tomada de decisões.
• A relação entre todos os resultados possíveis pode ser representada graficamente.
• É muito conveniente encontrar a causa raiz de um problema.
• Torna mais fácil resolver problemas de probabilidade e estatística.
• Um diagrama em árvore ajuda a organizar ideias e analisar a situação.