Diferença menos significativa de fisher: definição + exemplo

Uma ANOVA unidirecional é usada para determinar se há ou não uma diferença estatisticamente significativa entre as médias de três ou mais grupos independentes.

As suposições usadas em uma ANOVA são as seguintes:

H ₀ : As médias são iguais para cada grupo.

_HA : Pelo menos uma das formas é diferente das outras.

Se o valor p da ANOVA estiver abaixo de um determinado nível de significância (como α = 0,05), podemos rejeitar a hipótese nula e concluir que pelo menos uma das médias do grupo é diferente das demais.

Mas para saber exatamente quais grupos são diferentes entre si, precisamos fazer um teste post-hoc.

Um teste post hoc comumente usado é o teste de diferença menos significativa de Fisher .

Para realizar este teste, primeiro calculamos a seguinte estatística de teste:

LSD = t _0,025 , _{DF w} * √ MS _W (1/n ₁ + 1/n ₁ )

Ouro:

• t _0,025 , _DFw : O valor t-crítico da tabela de distribuição t com α = 0,025 e DF _w corresponde aos graus de liberdade dentro dos grupos da tabela ANOVA.
• MS _W : Quadrados médios dentro dos grupos na tabela ANOVA.
• n ₁ , n ₂ : Os tamanhos das amostras de cada grupo

Podemos então comparar a diferença média entre cada grupo com esta estatística de teste. Se o valor absoluto da diferença média entre dois grupos for maior que a estatística do teste, podemos declarar que existe uma diferença estatisticamente significativa entre as médias dos grupos.

O exemplo a seguir mostra como realizar o teste de diferença menos significativa de Fisher na prática.

Exemplo: Teste de diferença de menor significância de Fisher

Suponha que um professor queira saber se três técnicas de estudo diferentes levam ou não a notas diferentes em testes entre os alunos. Para testar isso, ela designa aleatoriamente 10 alunos para usar cada técnica de estudo e registra os resultados dos exames.

A tabela a seguir mostra os resultados dos exames de cada aluno com base na técnica de estudo utilizada:

O professor realiza uma ANOVA unidirecional e obtém os seguintes resultados:

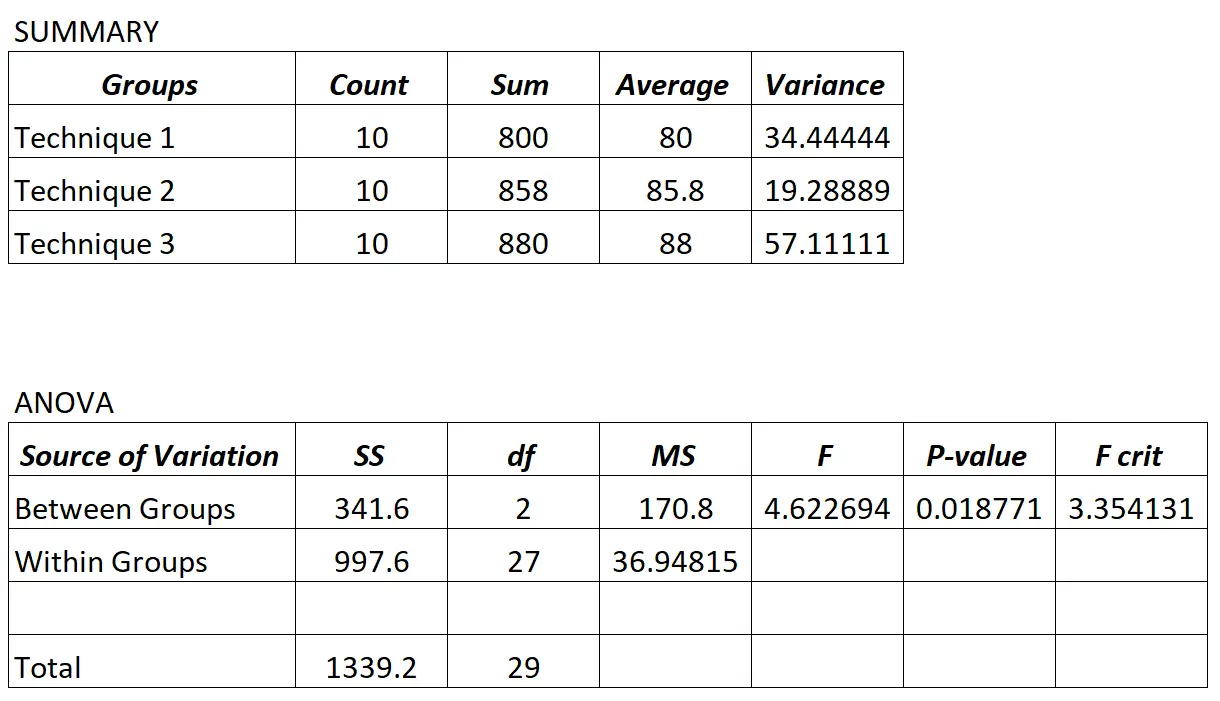
Como o valor p na tabela ANOVA (0,018771) é inferior a 0,05, podemos concluir que todas as notas médias dos exames entre os três grupos não são iguais.

Portanto, podemos fazer o teste de diferença menos significativa de Fisher para determinar quais médias de grupo são diferentes.

Usando os valores do resultado da ANOVA, podemos calcular a estatística do teste de Fisher da seguinte forma:

• LSD = t _0,025 , _DFw * √ MS _W (1/n ₁ + 1/n ₁ )
• LSD = t _0,025 , ₂₇ * √ 36,948*(1/10 + 1/10)
• LSD = 2,052 * √ 7,3896
• LSD = 5,578

Podemos então calcular a diferença média absoluta entre cada grupo:

• Técnica 1 versus Técnica 2: |80 – 85,8| = 5,8
• Técnica 1 versus Técnica 3: |80 – 88| = 8
• Técnica 2 versus Técnica 3: |85,8 – 88| = 2,2

As diferenças médias absolutas entre a técnica 1 e a técnica 2 e entre a técnica 1 e a técnica 3 são maiores que as estatísticas do teste de Fisher. Podemos, portanto, concluir que essas técnicas levam a pontuações médias nos exames estatisticamente significativamente diferentes.

Podemos também concluir que não há diferença significativa nas notas médias dos exames entre a técnica 2 e a técnica 3.