Distribuição de amostras

By Dr. benjamim anderson Agosto 3, 2023 Estatisticas 0 Comments

Este artigo explica o que é distribuição amostral em estatísticas e para que ela é usada. Assim você encontrará o significado de uma distribuição amostral, um exemplo concreto de distribuição amostral e, além disso, as fórmulas para os tipos mais comuns de distribuições amostrais.

Qual é a distribuição amostral?

A distribuição amostral , ou distribuição amostral , é a distribuição que resulta da consideração de todas as amostras possíveis de uma população. Em outras palavras, a distribuição amostral é a distribuição obtida calculando um parâmetro amostral de todas as amostras possíveis de uma população.

Por exemplo, se extrairmos todas as amostras possíveis de uma população estatística e calcularmos a média de cada amostra, o conjunto de médias amostrais forma uma distribuição amostral. Mais precisamente, como o parâmetro calculado é a média aritmética, é a distribuição amostral da média.

Nas estatísticas, a distribuição amostral é usada para calcular a probabilidade de aproximação do valor do parâmetro populacional ao estudar uma única amostra. Da mesma forma, a distribuição amostral nos permite estimar o erro amostral para um determinado tamanho de amostra.

Exemplo de distribuição de amostragem

Agora que conhecemos a definição de distribuição amostral, vejamos um exemplo simples para compreender totalmente o conceito.

Numa caixa colocamos três bolas e cada uma tem um número escrito de um a três, de forma que uma bola tem o número 1, outra bola tem o número 2 e a última bola tem o número 3. Para uma amostra de tamanho n = 2, calcula as probabilidades da distribuição amostral da média se forem selecionadas amostras com reposição.

As amostras são selecionadas com reposição, ou seja, a bola recolhida para selecionar o primeiro elemento da amostra é devolvida à caixa e pode ser selecionada novamente na segunda extração. Portanto, todas as amostras possíveis da população são:

1,1 1,2 1,3
2,1 2,2 2,3
3,1 3,2 3,3

Assim, calculamos a média aritmética de cada amostra possível:

$(1,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{11}=\cfrac{1+1}{2}=1$

$(1,2) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{12}=\cfrac{1+2}{2}=1,5$

$(1,3) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{13}=\cfrac{1+3}{2}=2$

$(2,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{21}=\cfrac{2+1}{2}=1,5$

$(2,2) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{22}=\cfrac{2+2}{2}=2$

$(2,3) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{23}=\cfrac{2+3}{2}=2,5$

$(3,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{31}=\cfrac{3+1}{2}=2$

$(3,2) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{32}=\cfrac{3+2}{2}=2,5$

$(3,3) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{33}=\cfrac{3+3}{2}=3$

Portanto, as probabilidades de obter cada valor da média amostral ao selecionar uma amostra aleatória da população são as seguintes:

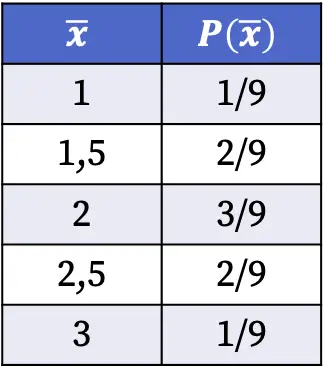
exemplo de tabela de distribuição de amostra

As probabilidades da distribuição amostral apresentadas na tabela acima foram calculadas dividindo o número de amostras com o referido valor médio pelo número total de casos possíveis. Por exemplo: a média amostral é 1,5 em dois casos entre nove possíveis, portanto P(1,5)=2/9.

Tipos de distribuições amostrais

As distribuições amostrais (ou distribuições amostrais) podem ser classificadas com base no parâmetro amostral a partir do qual foram obtidas. Portanto, os tipos mais comuns de distribuições são os seguintes:

Distribuição amostral da média : É a distribuição amostral que resulta do cálculo da média aritmética de cada amostra.
Distribuição Amostragem Proporcional : É a distribuição amostral obtida calculando a proporção de todas as amostras.
Distribuição amostral de variância : Esta é a distribuição amostral que forma o conjunto de todas as variâncias na amostra.
Distribuição amostral por diferença de médias : é a distribuição amostral que resulta do cálculo da diferença entre as médias de todas as amostras possíveis de duas populações diferentes.
Distribuição amostral por diferença de proporções : é a distribuição amostral obtida subtraindo todas as proporções amostrais possíveis de duas populações.

Cada tipo de distribuição amostral é explicado com mais detalhes abaixo.

Distribuição amostral da média

Dada uma população que segue uma distribuição de probabilidade normal com média

$\mu$

e desvio padrão

$\sigma$

e amostras de tamanho são extraídas

$n$

, a distribuição amostral da média também será definida por uma distribuição normal com as seguintes características:

$\begin{array}{c}\mu_{\overline{x}}=\mu \qquad \sigma_{\overline{x}}=\cfrac{\sigma}{\sqrt{n}}\\[4ex]\displaystyle N_{\overline{x}}\left(\mu, \frac{\sigma}{\sqrt{n}}\right) \end{array}$

Ouro

$\mu_{\overline{x}}$

é a média da distribuição amostral da média e

$\sigma_{\overline{x}}$

é o seu desvio padrão. Além disso,

$\cfrac{\sigma}{\sqrt{n}}$

é o erro padrão da distribuição amostral.

Nota: Se a população não seguir uma distribuição normal, mas o tamanho da amostra for grande (n>30), a distribuição amostral da média também pode ser aproximada à distribuição normal acima pelo limite do teorema central.

Portanto, como a distribuição amostral da média segue uma distribuição normal, a fórmula para calcular qualquer probabilidade relacionada à média amostral é:

$Z=\cfrac{\overline{x}-\mu}{\displaystyle\frac{\sigma}{\sqrt{n}}}$

Ouro:

$\overline{x}$

é a média amostral.
$\mu$

Esta é a média da população.
$s$

é o desvio padrão da população.
$n$

é o tamanho da amostra.
$Z$

é uma variável definida pela distribuição normal padrão N(0,1).

➤ Veja: Exercício resolvido sobre distribuição amostral da média

Distribuição amostral de proporção

Na verdade, quando estudamos uma proporção de uma amostra, analisamos casos de sucesso. Portanto, a variável aleatória em estudo segue uma distribuição de probabilidade binomial.

De acordo com o teorema do limite central, para tamanhos grandes (n>30) podemos aproximar uma distribuição binomial de uma distribuição normal. Portanto, a distribuição amostral da proporção se aproxima de uma distribuição normal com os seguintes parâmetros:

$\begin{array}{c}\displaystyle\mu_{p}=p \qquad \sigma_{p}=\sqrt{\frac{pq}{n}}\\[4ex]\displaystyle N_{p}\left(p, \sqrt{\frac{pq}{n}}\right) \end{array}$

Ouro

$p$

é a probabilidade de sucesso e

$q$

é a probabilidade de falha

$q=1-p$

Nota: Uma distribuição binomial só pode ser aproximada de uma distribuição normal se

$n>30″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”52″ style=”vertical-align: -2px;”></p> <p> ,</p> <p class=$ $np\ge 5$

$nq\ge 5$

Portanto, como a distribuição amostral da proporção pode ser aproximada a uma distribuição normal, a fórmula para calcular qualquer probabilidade relacionada à proporção de uma amostra é:

$Z=\cfrac{\widehat{p}-p}{\displaystyle\sqrt{\frac{pq}{n}}}$

Ouro:

$\widehat{p}$

é a proporção da amostra.
$p$

é a proporção da população.
$q$

é a probabilidade de falha da população,

$q=1-p$

.
$n$

é o tamanho da amostra.
$Z$

é uma variável definida pela distribuição normal padrão N(0,1).

➤ Veja: Exercício resolvido sobre distribuição amostral da proporção

Distribuição amostral de variância

A distribuição amostral de variância é definida pela distribuição de probabilidade qui-quadrado. Portanto, a fórmula para a estatística da distribuição amostral de variância é:

$\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

Ouro:

$\chi^2$

é a estatística da distribuição amostral de variância, que segue uma distribuição qui-quadrado.
$n$

é o tamanho da amostra.
$s^2$

é a variância da amostra.
$\sigma^2$

é a variância populacional.

➤ Veja: Exercício resolvido sobre distribuição amostral de variância

Distribuição amostral de diferença de médias

Se o tamanho da amostra for grande o suficiente (n ₁ ≥30 en ₂ ≥30), a distribuição amostral da diferença média segue uma distribuição normal. Mais precisamente, os parâmetros desta distribuição são calculados da seguinte forma:

$\begin{array}{c}\displaystyle \mu_{\overline{x_1}-\overline{x_2}}=\mu_1-\mu_2 \qquad \sigma_{\overline{x_1}-\overline{x_2}}=\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\\[6ex]\displaystyle N_{\overline{x_1}-\overline{x_2}}\left(\mu_1-\mu_2, \sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right) \end{array}$

Nota: Se ambas as populações forem distribuições normais, então a distribuição amostral da diferença nas médias segue uma distribuição normal, independentemente do tamanho da amostra.

Portanto, como a distribuição amostral da diferença de médias é definida por uma distribuição normal, a fórmula para calcular a estatística da distribuição amostral da diferença de médias é:

$Z=\cfrac{(\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}$

Ouro:

$\overline{x_i}$

é a média da amostra i.
$\mu_i$

é a média da população i.
$\sigma_i$

é o desvio padrão da população i.
$n_i$

é o tamanho da amostra i.
$Z$

é uma variável definida pela distribuição normal padrão N(0,1).

Observe que amostras de populações diferentes podem ter tamanhos de amostra diferentes.

➤ Veja: Exercício resolvido sobre distribuição amostral da diferença de médias

Distribuição amostral de diferença em proporções

As amostras selecionadas para a distribuição amostral por diferença de proporções são definidas por distribuições binomiais, porque para fins práticos uma proporção é uma razão entre casos de sucesso e o número total de observações.

No entanto, devido ao teorema do limite central, as distribuições binomiais podem ser aproximadas às distribuições normais de probabilidade. Portanto, a distribuição amostral da diferença de proporções pode ser aproximada a uma distribuição normal com as seguintes características:

$\begin{array}{c}\displaystyle\mu_{\widehat{p_1}-\widehat{p_2}}=p_1-p_2 \qquad \sigma_{\widehat{p_1}-\widehat{p_2}}=\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\\[6ex]\displaystyle N_{p}\left(p_1-p_2, \sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\right) \end{array}$

Nota: A distribuição amostral da diferença de proporções só pode ser aproximada de uma distribuição normal se

$n_1\geq30$

$n_2\geq 30$

$n_1p_1\geq5$

$n_2p_2\geq5$

$n_1q_1\geq5$

$n_2q_2\geq5$

Portanto, uma vez que a distribuição amostral da diferença de proporções pode ser aproximada de uma distribuição normal, a fórmula para calcular a estatística da distribuição amostral da diferença de proporções é a seguinte:

$Z=\cfrac{(\widehat{p_1}-\widehat{p_2})-(p_1-p_2)}{\displaystyle\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}}$

Ouro:

$\widehat{p_i}$

é a proporção da amostra i.
$p_i$

é a proporção da população i.
$q_i$

é a probabilidade de falha da população i,

$q_i=1-p_i$

.
$n_i$

é o tamanho da amostra i.
$Z$

é uma variável definida pela distribuição normal padrão N(0,1).

➤ Veja: Exercício resolvido sobre distribuição amostral da diferença de proporções

About Author

Dr. benjamim anderson

Olá, sou Benjamin, um professor aposentado de estatística que se tornou professor dedicado na Statorials. Com vasta experiência e conhecimento na área de estatística, estou empenhado em compartilhar meu conhecimento para capacitar os alunos por meio de Statorials. Saber mais

Qual é a distribuição amostral?

Exemplo de distribuição de amostragem

Tipos de distribuições amostrais

Distribuição amostral da média

Distribuição amostral de proporção

Distribuição amostral de variância

Distribuição amostral de diferença de médias

Distribuição amostral de diferença em proporções

About Author

Dr. benjamim anderson

Add a Comment