Distribuição amostral de diferença em proporções

Este artigo explica qual é a diferença na distribuição amostral proporcional e para que ela é usada nas estatísticas. A fórmula de distribuição amostral por diferença de proporções e um exercício resolvido passo a passo também são apresentados.

Qual é a distribuição amostral da diferença de proporções?

A diferença na distribuição amostral de proporções é a distribuição que resulta do cálculo das diferenças entre as proporções amostrais de todas as amostras possíveis de duas populações diferentes.

Ou seja, o processo de obtenção da distribuição amostral da diferença de proporções consiste, em primeiro lugar, em extrair todas as amostras possíveis de duas populações diferentes, em segundo lugar, em determinar a proporção de cada amostra extraída e, por fim, em determinar a diferença entre todas as proporções da diferença de proporções. duas populações. Para que o conjunto de resultados obtidos após a realização dessas operações forme a distribuição amostral da diferença de proporções.

Nas estatísticas, a diferença na distribuição amostral de proporções é usada para calcular a probabilidade de que a diferença entre as proporções amostrais de duas amostras selecionadas aleatoriamente esteja próxima da diferença nas proporções populacionais.

Fórmula para distribuição amostral de diferença de proporções

As amostras selecionadas para a distribuição amostral por diferença de proporções são definidas por distribuições binomiais , pois para fins práticos, uma proporção é uma razão entre casos de sucesso e o número total de observações.

No entanto, devido ao teorema do limite central, as distribuições binomiais podem ser aproximadas às distribuições normais de probabilidade . Portanto, a distribuição amostral da diferença de proporções pode ser aproximada a uma distribuição normal com as seguintes características:

Nota: A distribuição amostral da diferença de proporções só pode ser aproximada de uma distribuição normal se

,

,

,

,

E

.

Portanto, uma vez que a distribuição amostral da diferença de proporções pode ser aproximada de uma distribuição normal, a fórmula para calcular a estatística da distribuição amostral da diferença de proporções é a seguinte:

Ouro:

• 

  é a proporção da amostra i.

• 

  é a proporção da população i.

• 

  é a probabilidade de falha da população i,

  

  .

• 

  é o tamanho da amostra i.

• 

  é uma variável definida pela distribuição normal padrão N(0,1).

Esta fórmula é semelhante à fórmula de teste de hipótese para diferença de proporções.

Exemplo concreto de distribuição amostral de diferença de proporções

Depois de ver a definição de Distribuição Amostragem por Diferença de Proporções e qual a sua fórmula, você confere abaixo um exemplo resolvido passo a passo para finalizar o entendimento do conceito.

• Você deseja analisar a precisão de duas plantas de produção, uma fábrica produz de tal forma que apenas 5% das peças produzidas apresentam defeitos, enquanto a porcentagem de peças defeituosas de outra fábrica é de 8%. Se tomarmos uma amostra de 200 peças da primeira fábrica e outra amostra de 280 peças da segunda fábrica, qual é a probabilidade de que a percentagem de defeitos na primeira fábrica seja maior que a percentagem de defeitos na segunda fábrica? Produção?

Para finalizar o conhecimento de todos os dados do problema, primeiro calcularemos a proporção de peças bem produzidas de cada planta:

Se a taxa de defeitos na primeira fábrica fosse maior que a taxa de defeitos na segunda fábrica, isso significa que a seguinte equação seria verdadeira:

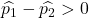
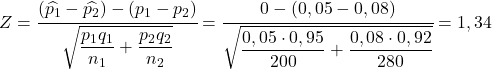
Assim, a probabilidade de a taxa de defeitos da primeira fábrica ser maior que a taxa de defeitos da segunda fábrica equivale à probabilidade da variável Z ser maior que 1,34:

tabela de distribuição normal e já teremos resolvido o problema:

➤ Veja: Distribuição amostral de diferença de médias