Distribuição amostral da média

Este artigo explica o que é a distribuição amostral da média nas estatísticas. Você também encontrará a fórmula de distribuição amostral média e um exercício resolvido passo a passo.

Qual é a distribuição amostral da média?

A distribuição amostral da média (ou distribuição amostral das médias ) é a distribuição que resulta do cálculo da média amostral de cada amostra possível de uma população. Ou seja, o conjunto de médias amostrais de todas as amostras possíveis de uma população forma a distribuição amostral da média.

Ou em outras palavras, se estudarmos todas as amostras que podem ser retiradas de uma população e calcularmos a média de cada uma das amostras, o conjunto de valores calculados forma uma distribuição amostral da média amostral.

Nas estatísticas, a distribuição amostral da média é usada para calcular a probabilidade de aproximação do valor da média da população ao analisar uma única amostra.

Fórmula para a distribuição amostral da média

Dada uma população que segue uma distribuição de probabilidade normal com média

e desvio padrão

e amostras de tamanho são extraídas

, a distribuição amostral da média também será definida por uma distribuição normal com as seguintes características:

Ouro

é a média da distribuição amostral da média e

é o seu desvio padrão. Além disso,

é o erro padrão da distribuição amostral.

Nota: Se a população não seguir uma distribuição normal, mas o tamanho da amostra for grande (n>30), a distribuição amostral da média também pode ser aproximada da distribuição normal anterior pelo teorema do limite central.

Portanto, como a distribuição amostral da média segue uma distribuição normal, a fórmula para calcular qualquer probabilidade relacionada à média amostral é:

Ouro:

• 

  é a média amostral.

• 

  Esta é a média da população.

• 

  é o desvio padrão da população.

• 

  é o tamanho da amostra.

• 

  é uma variável definida pela distribuição normal padrão N(0,1).

Exemplo do mundo real da distribuição amostral da média

Depois de ver a definição de distribuição amostral de média e quais são suas fórmulas associadas, vamos resolver um exemplo para entender melhor o conceito.

• O peso dos universitários segue distribuição normal com média de 68 kg e desvio padrão de 9 kg. Determinado:
  1. Qual é a probabilidade de que a média de uma amostra aleatória de 25 alunos seja inferior a 66 kg?
  2. Se forem colhidas 300 amostras com tamanho de 25 alunos cada, quantas médias amostrais terão valor inferior a 66 kg?

Em primeiro lugar devemos calcular o valor da estatística correspondente, para isso aplicamos a fórmula que vimos acima:

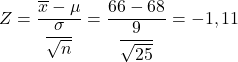
A probabilidade que procuramos é, portanto, aquela correspondente ao valor Z=-1,11 da cauda esquerda da distribuição normal padrão, que pode ser facilmente obtida na tabela de probabilidade Z. Portanto, usamos a tabela Z para determinar a probabilidade que o problema nos pede:

Agora que sabemos a probabilidade de que a média de uma amostra aleatória seja inferior a 66 kg, para saber a média do número de amostras inferior a 66 kg tomando 300 amostras iguais, precisamos multiplicar a probabilidade calculada pelo número total de amostras colhidas:

Portanto, aproximadamente 40 das amostras extraídas terão em média menos de 66 kg.