Distribuição binomial

By Dr. benjamim anderson Agosto 3, 2023 Probabilidade 0 Comments

Este artigo explica o que é a distribuição binomial nas estatísticas e para que ela é usada. Você encontrará, portanto, a definição da distribuição binomial, exemplos de distribuições binomiais e as propriedades deste tipo de distribuição de probabilidade. Além disso, você poderá calcular qualquer probabilidade da distribuição binomial com uma calculadora online.

Qual é a distribuição binomial?

A distribuição binomial é uma distribuição de probabilidade que conta o número de sucessos ao realizar uma série de experimentos independentes e dicotômicos com uma probabilidade de sucesso constante.

Em outras palavras, a distribuição binomial é uma distribuição que descreve o número de resultados bem-sucedidos de uma sequência de tentativas de Bernoulli.

Lembre-se de que um teste de Bernoulli é um experimento que tem dois resultados possíveis: “sucesso” e “fracasso”. Portanto, se a probabilidade de “sucesso” for p , a probabilidade de “fracasso” é q=1-p .

Em geral, o número total de experimentos realizados é definido com o parâmetro n , enquanto p é a probabilidade de sucesso de cada experimento. Assim, uma variável aleatória que segue uma distribuição binomial é escrita da seguinte forma:

$X\sim\text{Bin}(n,p)$

Observe que em uma distribuição binomial, exatamente o mesmo experimento é repetido n vezes e os experimentos são independentes um do outro, portanto a probabilidade de sucesso de cada experimento é a mesma (p) .

A distribuição binomial também pode ser chamada de distribuição binomial .

Exemplos de distribuição binomial

Depois de vermos a definição da distribuição binomial, veremos vários exemplos de variáveis que seguem este tipo de distribuição para melhor compreender o conceito.

Número de vezes que aparece cara ao lançar uma moeda 25 vezes.
Número de arremessos dados por um jogador de basquete ao arremessar 60 vezes em direção à cesta do mesmo local.
Número de vezes que obtemos o número 6 lançando um dado 30 vezes.
Número de aprovações de um total de 50 alunos fazendo um exame.
Número de unidades defeituosas em uma amostra de 100 produtos.

Fórmula de distribuição binomial

Dados os parâmetros x, n, p, a função de probabilidade da distribuição binomial é definida como o número combinatório de n em x vezes p ^x vezes (1-p) ^nx .

Portanto, a fórmula para calcular a probabilidade de uma distribuição binomial é:

👉 Você pode usar a calculadora abaixo para calcular a probabilidade de uma variável que segue a distribuição binomial.

Por outro lado, a probabilidade cumulativa da distribuição binomial é calculada somando as probabilidades do número de casos de sucesso em questão e todas as probabilidades anteriores. Portanto, a fórmula para calcular uma probabilidade cumulativa de uma distribuição binomial é:

$\displaystyle P[X\leq x]=\sum_{k=0}^x\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k}$

Exercício resolvido sobre distribuição binomial

Lançamos uma moeda 10 vezes, qual é a probabilidade de obter 6 caras?

A variável neste problema segue uma distribuição binomial porque todos os lançamentos são independentes entre si e também têm a mesma probabilidade de sucesso.

Concretamente, a probabilidade de sucesso é de 50%, uma vez que apenas um dos dois resultados possíveis é considerado um sucesso.

$p=\cfrac{1}{2}=0,5$

Portanto, a distribuição para este exercício é um binômio com um total de 10 experimentos e uma probabilidade de 0,5.

$X\sim\text{Bin}(10 ; 0,5)$

Portanto, para determinar a probabilidade de obter seis caras, precisamos aplicar a fórmula de distribuição binomial.

$\begin{aligned}P[X=x]&=\begin{pmatrix}n\\x\end{pmatrix}p^x(1-p)^{n-x}\\[2ex]P[X=6]&=\begin{pmatrix}10\\6\end{pmatrix}0,5^6(1-0,5)^{10-6}\\[2ex]P[X=6]&=0,2051\end{aligned}$

Portanto, a probabilidade de obter exatamente seis caras jogando uma moeda dez vezes é de 20,51%.

Características da distribuição binomial

A distribuição binomial possui as seguintes características:

A distribuição binomial é definida com dois parâmetros: n é o número total de experimentos de Bernoulli e, por outro lado, p é a probabilidade de sucesso de cada experimento de Bernoulli.

$\begin{array}{c}X\sim\text{Bin}(n,p)\\[2ex]n\geq 0\\[2ex]0\leq p\leq 1\end{array}$

A média de uma distribuição binomial é igual ao produto do número total de experimentos multiplicado pela probabilidade de sucesso de cada experimento. Portanto, para calcular a média de uma distribuição binomial, deve-se multiplicar n por p .

$E[X]=n\cdot p$

A variância de uma distribuição binomial é igual ao número total de tentativas multiplicado pela probabilidade de sucesso e pela probabilidade de fracasso.

$Var(X)=n\cdot p\cdot (1-p)$

A fórmula para a função de probabilidade da distribuição binomial é a seguinte:

$\displaystyle P[X=x]&=\begin{pmatrix}n\\ x\end{pmatrix}p^x(1-p)^{n-x}$

Da mesma forma, a fórmula para a função de distribuição cumulativa da distribuição binomial é:

$\displaystyle P[X\leq x]=\sum_{k=0}^x\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k}$

A soma de duas distribuições binomiais independentes com a mesma probabilidade é equivalente a uma distribuição binomial com o mesmo valor de probabilidade p e sendo n a soma do número total de tentativas das duas distribuições.

$\begin{array}{c}X\sim\text{Bin}(n,p)\qquad Y\sim\text{Bin}(m,p)\\[4ex]Z=X+Y \sim\text{Bin}(n+m,p)\end{array}$

$\displaystyle P[Z=z]=\begin{pmatrix}n+m\\z\end{pmatrix}p^z(1-p)^{n+m-z}$

A distribuição de Bernoulli é um caso especial de distribuição binomial em que n=1 , ou seja, apenas um experimento é realizado.

$X\sim\text{Bin}(1,p) \quad \color{orange}\bm{\longrightarrow}\color{black}\quad X\sim\text{Bernoulli}(p)$

_Se _X 1 , _X ₂ ,…, X _k são variáveis aleatórias independentes tais que

$\displaystyle\sum_{i=1}^k X_i\sim \text{Bin}\left(\sum_{i=1}^k n_i,p\right)$

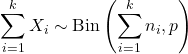
Calculadora de distribuição binomial

Insira os valores dos parâmetros p, n e x da distribuição binomial na calculadora a seguir para calcular a probabilidade. Você precisa selecionar a probabilidade que deseja calcular e inserir os números usando o ponto como separador decimal, por exemplo 0,1667.

About Author

Dr. benjamim anderson

Olá, sou Benjamin, um professor aposentado de estatística que se tornou professor dedicado na Statorials. Com vasta experiência e conhecimento na área de estatística, estou empenhado em compartilhar meu conhecimento para capacitar os alunos por meio de Statorials. Saber mais