Como usar distribuição binomial em python

A distribuição binomial é uma das distribuições mais comumente usadas em estatística. Descreve a probabilidade de obter k sucessos em n experimentos binomiais.

Se uma variável aleatória X segue uma distribuição binomial, então a probabilidade de X = k sucesso pode ser encontrada pela seguinte fórmula:

P(X=k) = _n C _k * p ^k * (1-p) ^nk

Ouro:

• n: número de tentativas
• k: número de sucessos
• p: probabilidade de sucesso em uma determinada tentativa
• _n C _k : o número de maneiras de obter k sucessos em n tentativas

Este tutorial explica como usar a distribuição binomial em Python.

Como gerar uma distribuição binomial

Você pode gerar uma matriz de valores que segue uma distribuição binomial usando a função random.binomial da biblioteca numpy:

 from numpy import random

#generate an array of 10 values that follows a binomial distribution
random.binomial(n=10, p=.25, size=10)

array([5, 2, 1, 3, 3, 3, 2, 2, 1, 4])

Cada número na tabela resultante representa o número de “sucessos” encontrados ao longo de 10 tentativas, onde a probabilidade de sucesso em uma determinada tentativa era de 0,25 .

Como calcular probabilidades usando uma distribuição binomial

Você também pode responder perguntas sobre probabilidade binomial usando a função binom da biblioteca scipy.

Pergunta 1: Nathan acerta 60% de suas tentativas de lance livre. Se ele acertar 12 lances livres, qual é a probabilidade de acertar exatamente 10?

 from scipy.stats import binom

#calculate binomial probability
binom.pmf(k= 10 , n= 12 , p= 0.6 )

0.0639

A probabilidade de Nathan acertar exatamente 10 lances livres é 0,0639 .

Questão 2: Marty joga uma moeda honesta 5 vezes. Qual é a probabilidade de a moeda dar cara 2 vezes ou menos?

 from scipy.stats import binom

#calculate binomial probability
binom.cdf(k= 2 , n= 5 , p= 0.5 )

0.5

A probabilidade de a moeda dar cara 2 vezes ou menos é de 0,5 .

Pergunta 3: Sabemos que 70% dos indivíduos apoiam uma determinada lei. Se 10 indivíduos forem selecionados aleatoriamente, qual é a probabilidade de que entre 4 e 6 deles apoiem a lei?

 from scipy.stats import binom

#calculate binomial probability
binom.cdf(k= 6 , n= 10 , p= 0.7 ) - binom.cdf(k= 3 , n= 10 , p= 0.7 )

0.3398

A probabilidade de que entre 4 e 6 indivíduos selecionados aleatoriamente apoiem a lei é de 0,3398 .

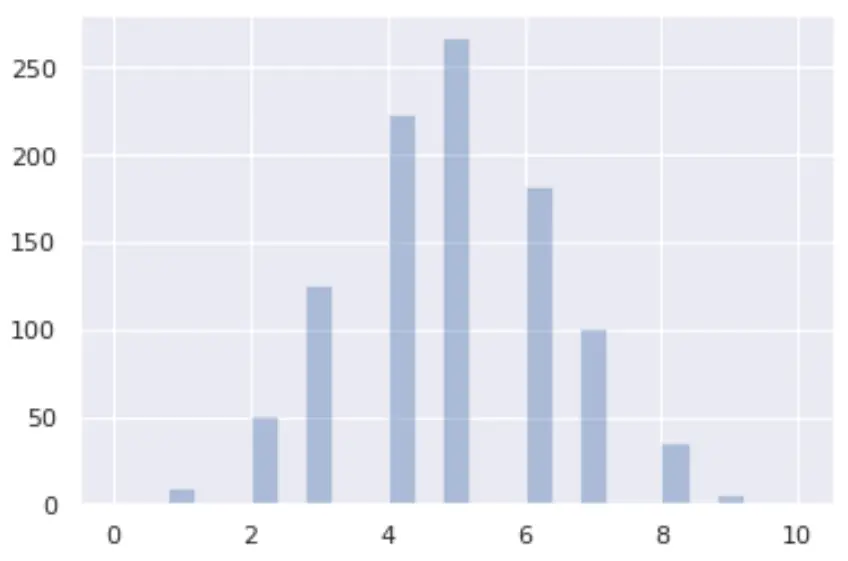
Como visualizar uma distribuição binomial

Você pode visualizar uma distribuição binomial em Python usando as bibliotecas seaborn e matplotlib :

 from numpy import random
import matplotlib.pyplot as plt
import seaborn as sns

x = random.binomial(n= 10 , p= 0.5 , size= 1000 )

sns.distplot(x, hist= True , kde= False )

plt.show()

Chá