Distribuição t de estudante
Este artigo explica o que é a distribuição t de Student e para que ela é usada. Além disso, é mostrado o gráfico da distribuição t de Student e quais são as características desse tipo de distribuição de probabilidade.
Qual é a distribuição do aluno?
A distribuição t de Student é uma distribuição de probabilidade amplamente utilizada em estatística. Especificamente, a distribuição t de Student é utilizada no teste t de Student para determinar a diferença entre as médias de duas amostras e para estabelecer intervalos de confiança.
A distribuição t de Student foi desenvolvida pelo estatístico William Sealy Gosset em 1908 sob o pseudônimo de “Student”.
A distribuição t de Student é definida pelo seu número de graus de liberdade, obtido subtraindo uma unidade do número total de observações. Portanto, a fórmula para determinar os graus de liberdade de uma distribuição t de Student é ν=n-1 .
![Rendered by QuickLaTeX.com \begin{array}{c}\nu=n-1\\[2ex]X\sim t_\nu\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-1c805dc2d6ca050feb70dad99de53402_l3.png)
Gráfico de distribuição t de Student
Agora que conhecemos a definição da distribuição t de Student, vamos ver qual é o seu gráfico. Assim, a seguir você pode ver graficamente vários exemplos de distribuições t de Student com diferentes graus de liberdade.
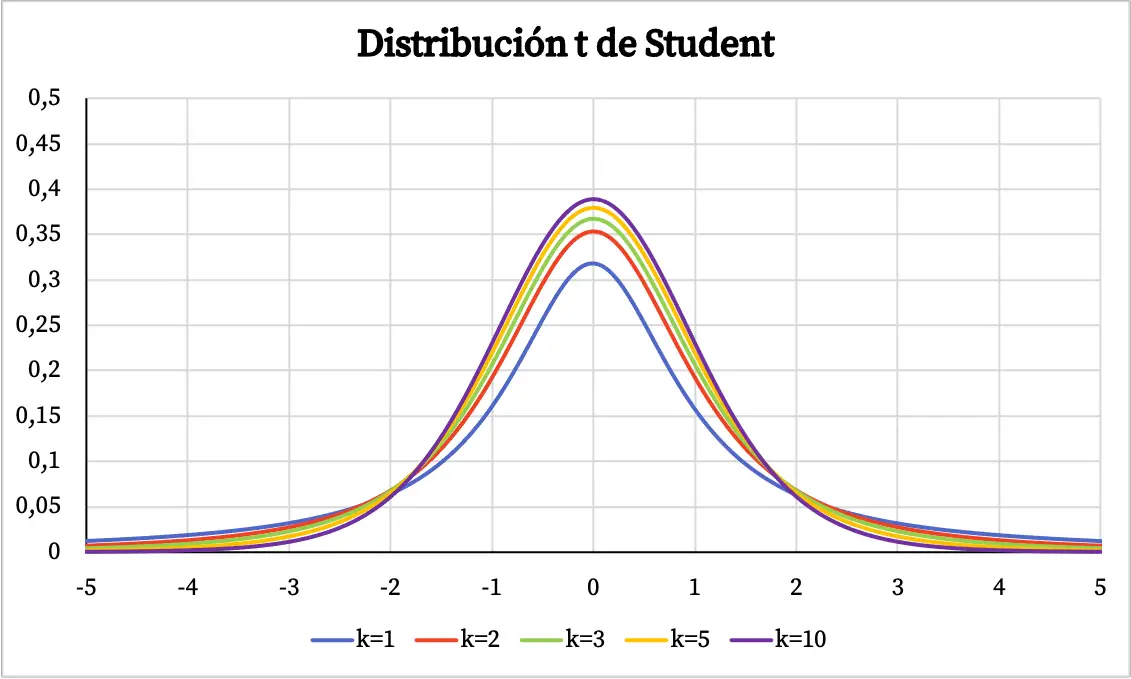
A partir do gráfico da distribuição t de Student, as seguintes propriedades podem ser deduzidas:
- A distribuição t de Student é simétrica centrada em 0 e tem formato de sino.
- A distribuição t de Student é mais dispersa que a distribuição normal, ou seja, a curva da distribuição t de Student é mais larga.
- Quanto mais graus de liberdade a distribuição t de Student tiver, menor será sua dispersão.
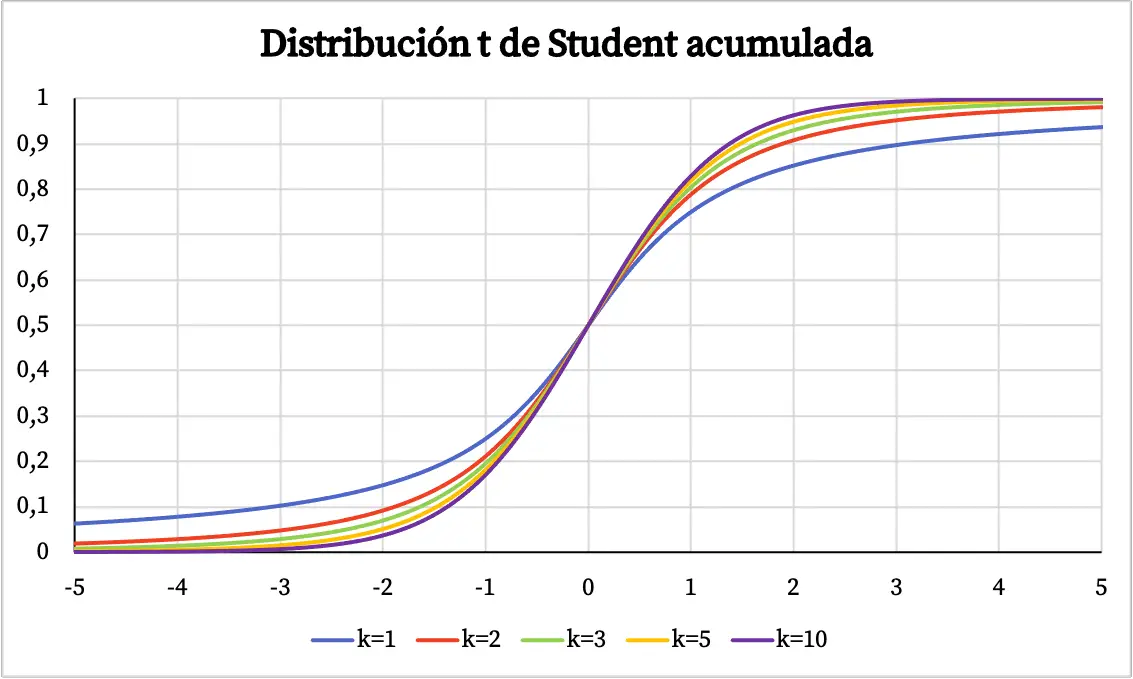
No gráfico acima, a função densidade da distribuição t de Student foi plotada em relação aos seus graus de liberdade. No entanto, você pode ver abaixo como a função de probabilidade cumulativa da distribuição t de Student varia:
Características da distribuição t de Student
As características mais importantes da distribuição t de Student são mostradas abaixo.
- O domínio da distribuição t de Student consiste em números reais.
![]()
- Para distribuições t de Student com mais de um grau de liberdade, a média da distribuição é igual a 0.
![\begin{array}{c}X\sim t_\nu\\[2ex] E[X]=0 \qquad \text{para }\nu>1\end{array} ” title=”Rendered by QuickLaTeX.com” height=”55″ width=”190″ style=”vertical-align: 0px;”></p>
</p>
<ul>
<li> A variância de uma distribuição t de Student pode ser calculada usando a seguinte expressão:</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-d4fed5eadcaa1162752aeedb7f8a0906_l3.png)
![\begin{array}{c}X\sim t_\nu\\[2ex] Var(X)=\cfrac{\nu}{\nu-2} \qquad \text{para }\nu>2\end{array} ” title=”Rendered by QuickLaTeX.com” height=”75″ width=”245″ style=”vertical-align: 0px;”></p>
</p>
<ul>
<li> A mediana e a moda da distribuição t de Student, independentemente do número de graus de liberdade, são sempre 0.</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-bfdcbc8a5f071a61e091b0ef6f686a16_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{c}Me=0\\[2ex]Mo=0\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-8d90790fce0c987648c0b30216c82214_l3.png)
- A função densidade da distribuição t de Student é definida pela seguinte fórmula:
![]()
- A função de distribuição de probabilidade cumulativa da distribuição t de Student é definida pela seguinte fórmula:
![Rendered by QuickLaTeX.com \displaystyle P[X\leq x]=\frac{1}{2} + x \Gamma \left( \frac{\nu+1}{2} \right) \cdot\frac{\,_2F_1 \left ( \frac{1}{2},\frac{\nu+1}{2};\frac{3}{2};-\frac{x^2}{\nu} \right)}{\sqrt{\pi\nu}\,\Gamma \left(\frac{\nu}{2}\right)}](https://statorials.org/wp-content/ql-cache/quicklatex.com-da1e3bdf2d87c3a7dcc89c236958dcec_l3.png)
- Para distribuições t de Student com graus de liberdade superiores a 3, o coeficiente de assimetria é zero porque é uma distribuição simétrica.
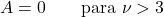
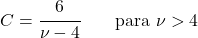 Aplicações da distribuição t de Student
Aplicações da distribuição t de Student
A distribuição t de Student é uma distribuição de probabilidade amplamente utilizada em estatística. Na verdade, existe até o teste t de Student, que é utilizado para testar hipóteses e intervalos de confiança.
Assim, a distribuição t de Student permite analisar a diferença entre as médias de duas amostras, mais precisamente, é utilizada para determinar se duas amostras possuem médias significativamente diferentes. Da mesma forma, o teste t de Student é utilizado para saber se a reta obtida a partir de uma análise de regressão linear tem inclinação ou não.
Em suma, as aplicações da distribuição t de Student baseiam-se na análise de conjuntos de dados que teoricamente seguem uma distribuição normal, mas o número total de observações é demasiado pequeno para utilizar este tipo de distribuição.