O que é uma distribuição amostral?

Imagine que há uma população de 10.000 golfinhos e o peso médio de um golfinho nessa população é de 300 libras.

Se tomarmos uma amostra aleatória simples de 50 golfinhos desta população, poderemos descobrir que o peso médio dos golfinhos nesta amostra é de 305 libras.

Então, se tomarmos outra amostra aleatória simples de 50 golfinhos, poderemos descobrir que o peso médio dos golfinhos nesta amostra é de 295 libras.

Sempre que tomamos uma amostra aleatória simples de 50 golfinhos, é provável que o peso médio dos golfinhos na amostra esteja próximo da média populacional de 300 libras, mas não exatamente de 300 libras.

Vamos imaginar que pegamos 200 amostras aleatórias simples de 50 golfinhos dessa população e criamos um histograma do peso médio de cada amostra:

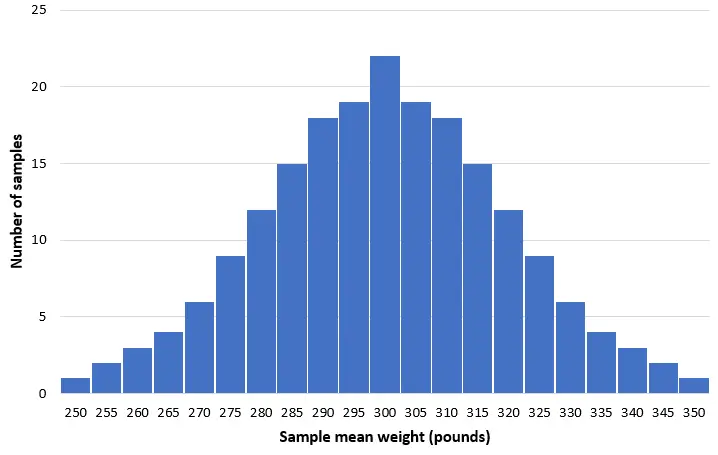
Na maioria das amostras, o peso médio será próximo a 300 libras. Em casos raros, podemos colher uma amostra cheia de pequenos golfinhos cujo peso médio é de apenas 250 quilos. Ou podemos pegar uma amostra cheia de golfinhos-nariz-de-garrafa que pesam em média 350 libras. Em geral, a distribuição das médias amostrais será aproximadamente normal, com o centro da distribuição localizado no verdadeiro centro da população.

Esta distribuição de médias amostrais é conhecida como distribuição amostral da média e tem as seguintes propriedades:

_µx = µ

onde μ _x é a média amostral e μ é a média populacional.

_σx = σ/√n

onde σ _x é o desvio padrão da amostra, σ é o desvio padrão da população e n é o tamanho da amostra.

Por exemplo, nesta população de golfinhos, sabemos que o peso médio é μ = 300. Portanto, a média da distribuição amostral é μ _x = 300 .

Suponha que também saibamos que o desvio padrão da população é de 18 libras. O desvio padrão da amostra é, portanto , σ _x = 18/ √50 = 2,546 .

Distribuição amostral de proporção

Considere a mesma população de 10.000 golfinhos. Suponha que 10% dos golfinhos sejam pretos e o restante cinza. Suponha que tomemos uma amostra aleatória simples de 50 golfinhos e descubramos que 14% dos golfinhos nessa amostra são pretos. A seguir, pegamos outra amostra aleatória simples de 50 golfinhos e descobrimos que 8% dos golfinhos nesta amostra são pretos.

Imagine que pegamos 200 amostras aleatórias simples de 50 golfinhos desta população e criamos um histograma da proporção de golfinhos pretos em cada amostra:

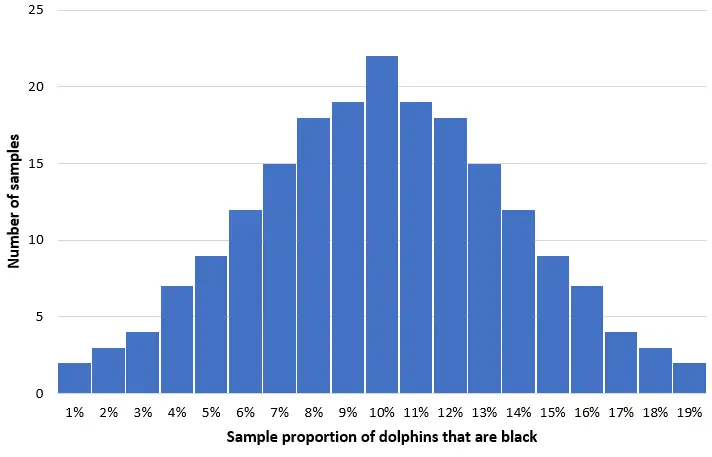
Na maioria das amostras, a proporção de golfinhos negros estará próxima da população real de 10%. A distribuição da proporção amostral de golfinhos negros será aproximadamente normal, com o centro da distribuição localizado no verdadeiro centro da população.

Esta distribuição de proporções amostrais é conhecida como distribuição amostral de proporção e tem as seguintes propriedades:

_µp = P

onde p é a proporção da amostra e P é a proporção da população.

σ _p = √ (P)(1-P) / n

onde P é a proporção da população en é o tamanho da amostra.

Por exemplo, nesta população de golfinhos sabemos que a verdadeira proporção de golfinhos negros é 10% = 0,1. Assim, a média da distribuição amostral proporcional é μ _p = 0,1 .

Suponha que também saibamos que o desvio padrão da população é de 18 libras. Assim, o desvio padrão da amostra é σ _p = √ (P)(1-P) / n = √ (.1)(1-.1) / 50 = .042 .

Estabeleça a normalidade

Para usar as fórmulas acima, a distribuição amostral deve ser normal.

De acordo com o teorema do limite central , a distribuição amostral de uma média amostral é aproximadamente normal se o tamanho da amostra for grande o suficiente, mesmo que a distribuição populacional não seja normal . Na maioria dos casos, consideramos que um tamanho de amostra de 30 ou mais é suficientemente grande.

A distribuição amostral de uma proporção amostral é aproximadamente normal se o número esperado de sucessos e falhas for pelo menos 10.

Exemplos

Podemos usar distribuições amostrais para calcular probabilidades.

Exemplo 1: Uma determinada máquina cria cookies. A distribuição de peso desses biscoitos é inclinada para a direita com média de 10 onças e desvio padrão de 2 onças. Se tomarmos uma amostra aleatória simples de 100 biscoitos produzidos por esta máquina, qual é a probabilidade de que o peso médio dos biscoitos nesta amostra seja inferior a 9,8 onças?

Etapa 1: Estabeleça a normalidade.

Precisamos garantir que a distribuição amostral das médias amostrais seja normal. Como o tamanho da nossa amostra é maior ou igual a 30, de acordo com o teorema do limite central, podemos assumir que a distribuição amostral das médias amostrais é normal.

Etapa 2: Encontre a média e o desvio padrão da distribuição amostral.

_µx = µ

_σx = σ/√n

μ _x = 10 onças

σ _x = 2/ √100 = 2/10 = 0,2 onças

Etapa 3: Use a calculadora de área de pontuação Z para determinar a probabilidade de que o peso médio do biscoito nesta amostra seja inferior a 9,8 onças.

Insira os seguintes números na calculadora da área de pontuação Z. Você pode deixar “Pontuação Bruta 2” em branco, pois encontramos apenas um número neste exemplo.

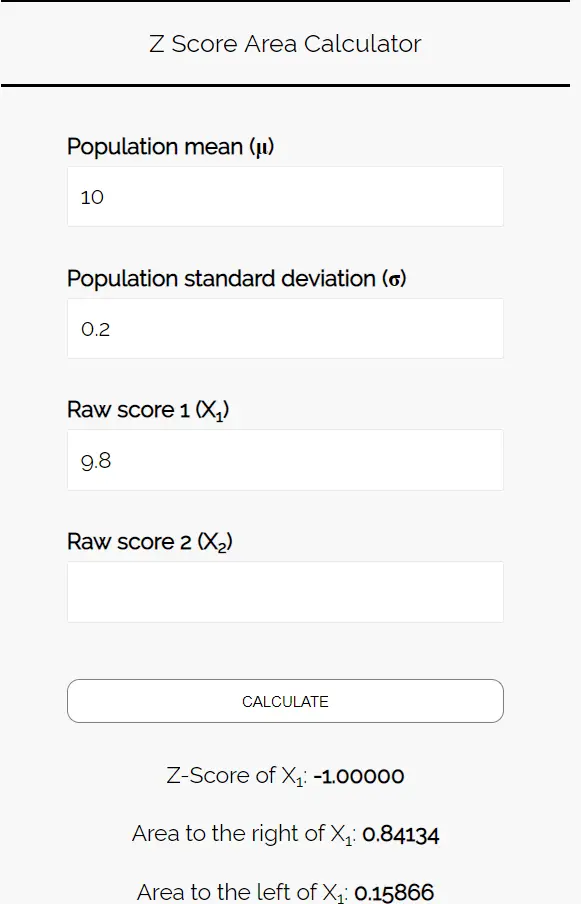
Como queremos saber a probabilidade de o peso médio dos biscoitos nesta amostra ser inferior a 9,8 onças, estamos interessados na área à esquerda de 9,8. A calculadora nos diz que essa probabilidade é 0,15866 .

Exemplo 2: De acordo com um estudo realizado em toda a escola, 87% dos alunos de uma determinada escola preferem pizza a sorvete. Suponha que tomemos uma amostra aleatória simples de 200 alunos. Qual é a probabilidade de que a proporção de estudantes que preferem pizza seja inferior a 85%?

Etapa 1: Estabeleça a normalidade.

Lembre-se de que a distribuição amostral de uma proporção amostral é aproximadamente normal se o número esperado de “sucessos” e “fracassos” for pelo menos 10.

Nesse caso, o número esperado de alunos que preferirão pizza é de 87% * 200 alunos = 174 alunos. O número esperado de alunos que não preferirão pizza é de 13% * 200 alunos = 26 alunos. Como ambos os números são pelo menos 10, podemos assumir que a distribuição amostral da proporção de alunos que preferirão pizza é aproximadamente normal.

Etapa 2: Encontre a média e o desvio padrão da distribuição amostral.

_µp = P

σ _p = √ (P)(1-P) / n

_µp = 0,87

_σp = √ (0,87)(1-0,87) / 200 = 0,024

Etapa 3: Use a calculadora de área de pontuação Z para determinar a probabilidade de que a proporção de alunos que preferem pizza seja inferior a 85%.

Insira os seguintes números na calculadora da área de pontuação Z. Você pode deixar “Pontuação Bruta 2” em branco, pois encontramos apenas um número neste exemplo.

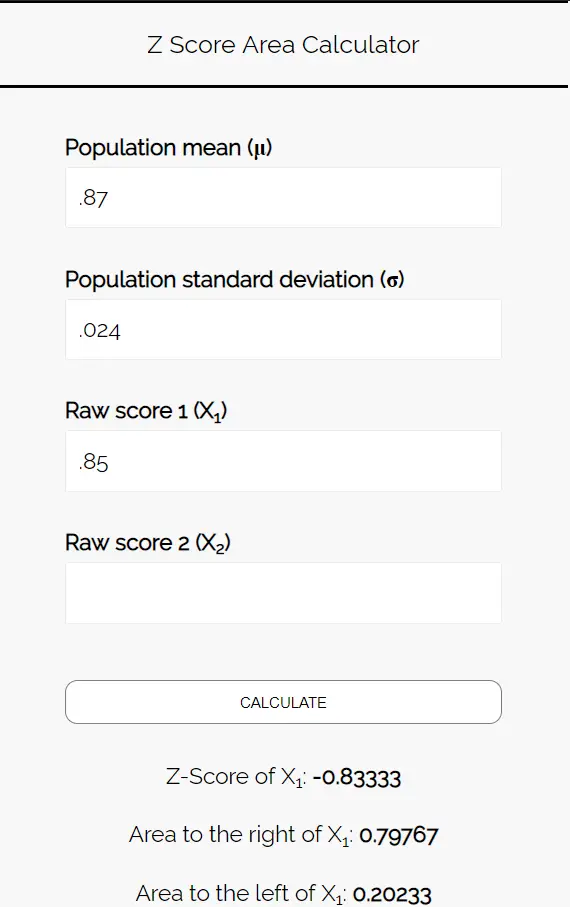
Como queremos saber a probabilidade de a proporção de estudantes que preferem pizza ser inferior a 85%, estamos interessados na área à esquerda de 0,85. A calculadora nos diz que essa probabilidade é 0,20233 .