Uma introdução à distribuição de poisson

A distribuição de Poisson é uma das distribuições mais populares em estatística.

Para compreender a distribuição de Poisson, é útil primeiro compreender os experimentos de Poisson.

Experimentos com peixes

Um experimento de Poisson é um experimento que possui as seguintes propriedades:

• O número de sucessos do experimento pode ser contado.
• O número médio de sucessos que ocorreram durante um intervalo de tempo (ou espaço) específico é conhecido.
• Cada resultado é independente.
• A probabilidade de ocorrência de sucesso é proporcional ao tamanho do intervalo.

Um exemplo de experimento de Poisson é o número de nascimentos por hora em um determinado hospital. Por exemplo, suponha que um determinado hospital tenha em média 10 partos por hora. Este é um experimento de Poisson porque possui as quatro propriedades a seguir:

• O número de sucessos do experimento pode ser contado – Podemos contar o número de nascimentos.
• É conhecido o número médio de nascimentos que ocorrem durante um intervalo de tempo específico – Sabe-se que ocorrem em média 10 nascimentos por hora.
• Cada resultado é independente – A probabilidade de uma mãe dar à luz em uma determinada hora é independente da probabilidade de outra mãe dar à luz.
• A probabilidade de ocorrer um sucesso é proporcional ao tamanho do intervalo: quanto maior o intervalo de tempo, maior a probabilidade de ocorrer um nascimento.

Podemos usar a distribuição de Poisson para responder questões sobre probabilidades sobre este experimento de Poisson, tais como:

• Qual é a probabilidade de ocorrerem mais de 12 nascimentos em uma determinada hora?
• Qual é a probabilidade de ocorrerem menos de 5 nascimentos em uma determinada hora?
• Qual é a probabilidade de que ocorram entre 8 e 11 nascimentos em uma determinada hora?

A distribuição dos peixes

A distribuição de Poisson descreve a probabilidade de obter k sucessos durante um determinado intervalo de tempo.

Se umavariável aleatória X segue uma distribuição de Poisson, então a probabilidade de X = k sucesso pode ser encontrada pela seguinte fórmula:

P(X=k) = λ ^k * e ^{– λ} / k!

Ouro:

• λ: número médio de sucessos ocorridos durante um intervalo específico
• k: número de sucessos
• e: uma constante igual a aproximadamente 2,71828

Por exemplo, suponha que um determinado hospital tenha uma média de 2 partos por hora. Podemos usar a fórmula acima para determinar a probabilidade de ocorrer 0, 1, 2, 3 nascimentos, etc. em uma determinada hora:

P(X=0) = 2 ⁰ * e ^{– 2/0} ! = 0,1353

P(X=1) = 2 ¹ * e ^{– 2/1} ! = 0,2707

P(X=2) = 2 ² * e ^{– 2/2} ! = 0,2707

P(X=3) = 2 ³ * e ^{– 2/3} ! = 0,1805

Podemos calcular a probabilidade de qualquer número de nascimentos até o infinito. Em seguida, criamos um histograma simples para visualizar esta distribuição de probabilidade:

Cálculo de probabilidades cumulativas de Poisson

É simples calcular uma única probabilidade de Poisson (por exemplo, a probabilidade de um hospital ter 3 partos numa determinada hora) utilizando a fórmula acima, mas para calcular as probabilidades de Poisson cumulativas precisamos de adicionar probabilidades individuais.

Por exemplo, digamos que queremos saber a probabilidade de o hospital ter 1 ou menos partos numa determinada hora. Usaríamos a seguinte fórmula para calcular essa probabilidade:

P(X≤1) = P(X=0) + P(X=1) = 0,1353 + 0,2707 = 0,406

Isso é chamado de probabilidade cumulativa porque envolve a adição de múltiplas probabilidades. Podemos calcular a probabilidade cumulativa de ocorrer k ou menos nascimentos em uma determinada hora usando uma fórmula semelhante:

P(X≤0) = P(X=0) = 0,1353

P(X≤1) = P(X=0) + P(X=1) = 0,1353 + 0,2707 = 0,406

P(X≤2) = P(X=0) + P(X=1) + P(X=2) =0,1353 + 0,2707 + 0,2707 = 0,6767

Podemos calcular estas probabilidades cumulativas para qualquer número de nascimentos até ao infinito. Podemos então criar um histograma para visualizar esta distribuição de probabilidade cumulativa:

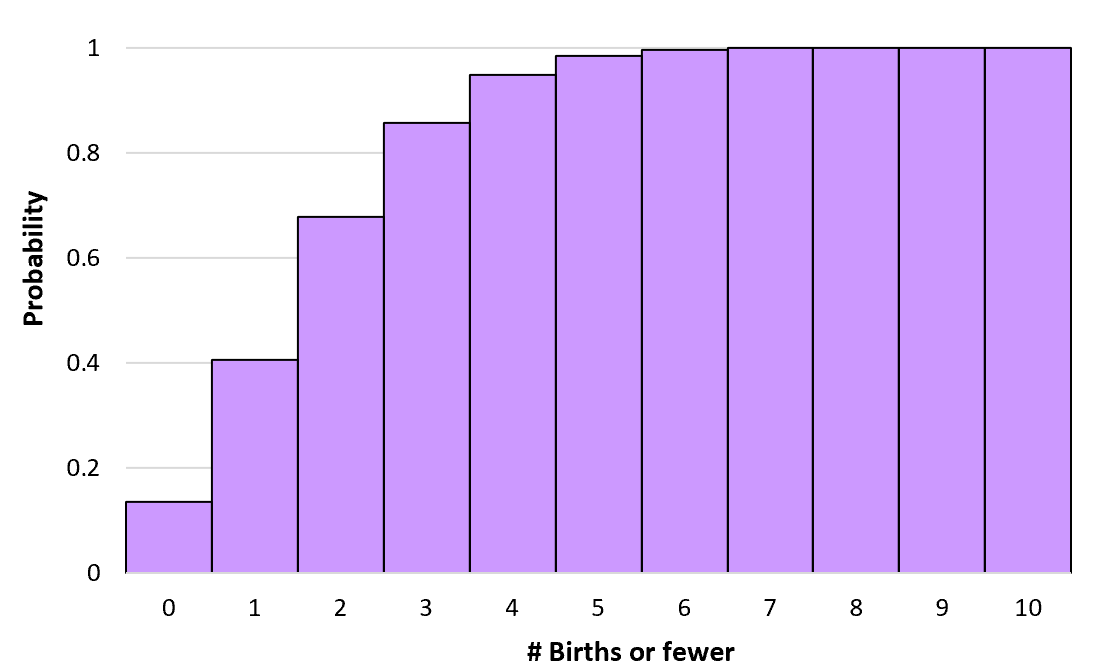
Propriedades da distribuição de Poisson

A distribuição de Poisson tem as seguintes propriedades:

A média da distribuição é λ .

A variância da distribuição também é λ .

O desvio padrão da distribuição é √ λ .

Por exemplo, suponha que um hospital tenha em média 2 partos por hora.

O número médio de nascimentos esperados em uma determinada hora é λ = 2 nascimentos.

A variação no número de nascimentos que esperamos é λ = 2 nascimentos.

Problemas de prática de distribuição de peixe

Use os seguintes problemas práticos para testar seu conhecimento sobre a distribuição de Poisson.

Nota: Usaremos a calculadora de distribuição de Poisson para calcular as respostas a estas perguntas.

Problema 1

Pergunta: Sabemos que um determinado site realiza 10 vendas por hora. Em uma determinada hora, qual é a probabilidade de o site realizar exatamente 8 vendas?

Resposta: Usando a calculadora de distribuição de Poisson com λ = 10 ex = 8, descobrimos que P(X=8) = 0,1126 .

Problema 2

Pergunta: Sabemos que uma determinada imobiliária realiza em média 5 vendas por mês. Em um determinado mês, qual a probabilidade de ela realizar mais de 7 vendas?

Resposta: Usando a calculadora de distribuição de Poisson com λ = 5 ex = 7, descobrimos que P(X>7) = 0,13337 .

Problema 3

Pergunta: Sabemos que um determinado hospital realiza 4 partos por hora. Numa determinada hora, qual é a probabilidade de ocorrerem 4 ou menos nascimentos?

Resposta: Usando a calculadora de distribuição de Poisson com λ = 4 ex = 4, descobrimos que P(X≤4) = 0,62884 .

Recursos adicionais

Os artigos a seguir explicam como usar a distribuição de Poisson em diferentes softwares estatísticos:

Como usar a distribuição de Poisson em R
Como usar a distribuição de Poisson no Excel
Como calcular probabilidades de Poisson em uma calculadora TI-84
Exemplos do mundo real da distribuição de Poisson
Calculadora de distribuição de peixes