Distribuição amostral de proporção

By Dr. benjamim anderson Agosto 3, 2023 Estatisticas 0 Comments

Este artigo explica o que é a distribuição amostral de proporção nas estatísticas. Da mesma forma, você encontrará a fórmula de distribuição amostral proporcional e, além disso, um exercício resolvido passo a passo.

Qual é a distribuição amostral da proporção?

A distribuição amostral de proporção (ou distribuição amostral de proporções ) é a distribuição que resulta do cálculo da proporção de cada amostra possível de uma população. Ou seja, as proporções amostrais de todas as amostras possíveis de uma população formam a distribuição amostral da proporção.

Em outras palavras, a distribuição amostral de proporção é obtida estudando todas as amostras que podem ser selecionadas de uma população e derivando a proporção amostral de cada amostra. Assim, o conjunto de proporções amostrais calculadas constitui a distribuição amostral da proporção.

Caso você esteja se perguntando para que serve a distribuição amostral de proporção, nas estatísticas ela é usada para calcular a probabilidade de se aproximar do valor da proporção populacional ao analisar uma única amostra.

➤ Veja: Distribuição amostral da média

Fórmula de distribuição de amostragem proporcional

Na verdade, quando estudamos uma proporção de uma amostra, analisamos casos de sucesso. Portanto, a variável aleatória em estudo segue uma distribuição de probabilidade binomial .

De acordo com o teorema do limite central, para tamanhos grandes (n>30) podemos aproximar uma distribuição binomial de uma distribuição normal. Portanto, a distribuição amostral da proporção se aproxima de uma distribuição normal com os seguintes parâmetros:

$\begin{array}{c}\displaystyle\mu_{p}=p \qquad \sigma_{p}=\sqrt{\frac{pq}{n}}\\[4ex]\displaystyle N_{p}\left(p, \sqrt{\frac{pq}{n}}\right) \end{array}$

Ouro

$p$

é a probabilidade de sucesso e

$q$

é a probabilidade de falha

$q=1-p$

Nota: Uma distribuição binomial só pode ser aproximada de uma distribuição normal se

$n>30″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”52″ style=”vertical-align: -2px;”> , <p class=$ $np\ge 5$

$nq\ge 5$

➤ Veja: Exemplos de distribuições normais

Portanto, como a distribuição amostral da proporção pode ser aproximada a uma distribuição normal, a fórmula para calcular qualquer probabilidade relacionada à proporção de uma amostra é:

$Z=\cfrac{\widehat{p}-p}{\displaystyle\sqrt{\frac{pq}{n}}}$

Ouro:

$\widehat{p}$

é a proporção da amostra.
$p$

é a proporção da população.
$q$

é a probabilidade de falha da população,

$q=1-p$

.
$n$

é o tamanho da amostra.
$Z$

é uma variável definida pela distribuição normal padrão N(0,1).

Exemplo concreto de distribuição de amostragem proporcional

Depois de vermos a definição de Distribuição de Amostragem Proporcional e quais são suas fórmulas associadas, um exemplo resolvido passo a passo é fornecido abaixo para uma compreensão completa do conceito.

Uma empresa industrial compra lotes de peças de uma fábrica que afirma produzir peças com apenas 3% de peças defeituosas. Para verificar isso, a empresa decide analisar um pedido de 500 peças. Qual é a probabilidade de encontrar mais de 5% de peças defeituosas na amostra?

Neste caso, a proporção da população que queremos estudar é 0,03, portanto o parâmetro q equivale a 0,97.

$\begin{array}{c}p=0,03\\[2ex]q=1-p=0,97\end{array}$

Assim, para encontrar a probabilidade que nos perguntam, devemos calcular a estatística correspondente aplicando a fórmula que vimos na seção anterior:

$Z=\cfrac{\widehat{p}-p}{\displaystyle\sqrt{\frac{pq}{n}}}=\cfrac{0,05-0,03}{\displaystyle\sqrt{\frac{0,03\cdot 0,97}{500}}}=2,62$

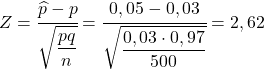
Assim, a probabilidade de obter mais de 5% de peças defeituosas é equivalente à seguinte probabilidade:

$P\left[\widehat{p}>0,05\right]=P[Z>2,62]=1-P[Z\leq 2,62]” title=”Rendered by QuickLaTeX.com” height=”19″ width=”360″ style=”vertical-align: -5px;”> Por fim, procuramos a probabilidade de P[Z≤2,62] na <a href=$ tabela de distribuição Z e calculamos a probabilidade que o problema nos pede:

$\begin{array}{l}P\left[\widehat{p}>0,05\right]=\\[2ex]=P[Z>2,62]=\\[2ex]=1-P[Z\leq 2,62]=\\[2ex]=1-0,9956=\\[2ex]=0,0044\end{array}” title=”Rendered by QuickLaTeX.com” height=”167″ width=”162″ style=”vertical-align: 0px;”> Concluindo, a probabilidade de encontrar mais de 5% de peças defeituosas na amostra analisada é de 0,44%. </div>  <div class=$

About Author

Dr. benjamim anderson

Olá, sou Benjamin, um professor aposentado de estatística que se tornou professor dedicado na Statorials. Com vasta experiência e conhecimento na área de estatística, estou empenhado em compartilhar meu conhecimento para capacitar os alunos por meio de Statorials. Saber mais

Qual é a distribuição amostral da proporção?

Fórmula de distribuição de amostragem proporcional

Exemplo concreto de distribuição de amostragem proporcional

About Author

Dr. benjamim anderson

Add a Comment