Uma introdução à distribuição exponencial

A distribuição exponencial é uma distribuição de probabilidade usada para modelar o tempo que temos que esperar até que um determinado evento ocorra.

Esta distribuição pode ser usada para responder perguntas como:

• Quanto tempo um varejista deve esperar que um cliente entre em sua loja?
• Por quanto tempo um laptop continuará funcionando antes de quebrar?
• Por quanto tempo a bateria de um carro continuará funcionando antes de morrer?
• Quanto tempo devemos esperar até a próxima erupção vulcânica numa determinada região?

Em cada cenário, queremos calcular quanto tempo teremos que esperar até que determinado evento ocorra. Assim, cada cenário poderia ser modelado usando uma distribuição exponencial.

Distribuição exponencial: PDF e CDF

Se uma variável aleatória X segue uma distribuição exponencial, então a função de densidade de probabilidade de X pode ser escrita:

f (x; λ) = λe ^-λx

Ouro:

• λ: o parâmetro de taxa (calculado como λ = 1/μ)
• e: Uma constante aproximadamente igual a 2,718

A função de distribuição cumulativa de

F (x; λ) = 1 – e ^-λx

Na prática, o CDF é mais frequentemente utilizado para calcular probabilidades relacionadas à distribuição exponencial.

Por exemplo, suponha que o número médio de minutos entre as erupções de um determinado gêiser seja de 40 minutos. Qual é a probabilidade de termos de esperar menos de 50 minutos por uma erupção?

Para resolver este problema, primeiro precisamos calcular o parâmetro de taxa:

• λ = 1/µ
• λ = 1/40
• λ = 0,025

Podemos inserir λ = 0,025 e x = 50 na fórmula CDF:

• P(X ≤ x) = 1 – e ^-λx
• P(X ≤ 50) = 1 – e ^-0,025(50)
• P(X ≤ 50) = 0,7135

A probabilidade de termos que esperar menos de 50 minutos pela próxima erupção é de 0,7135 .

Visualize a distribuição exponencial

O gráfico a seguir mostra a função de densidade de probabilidade de uma variável aleatória

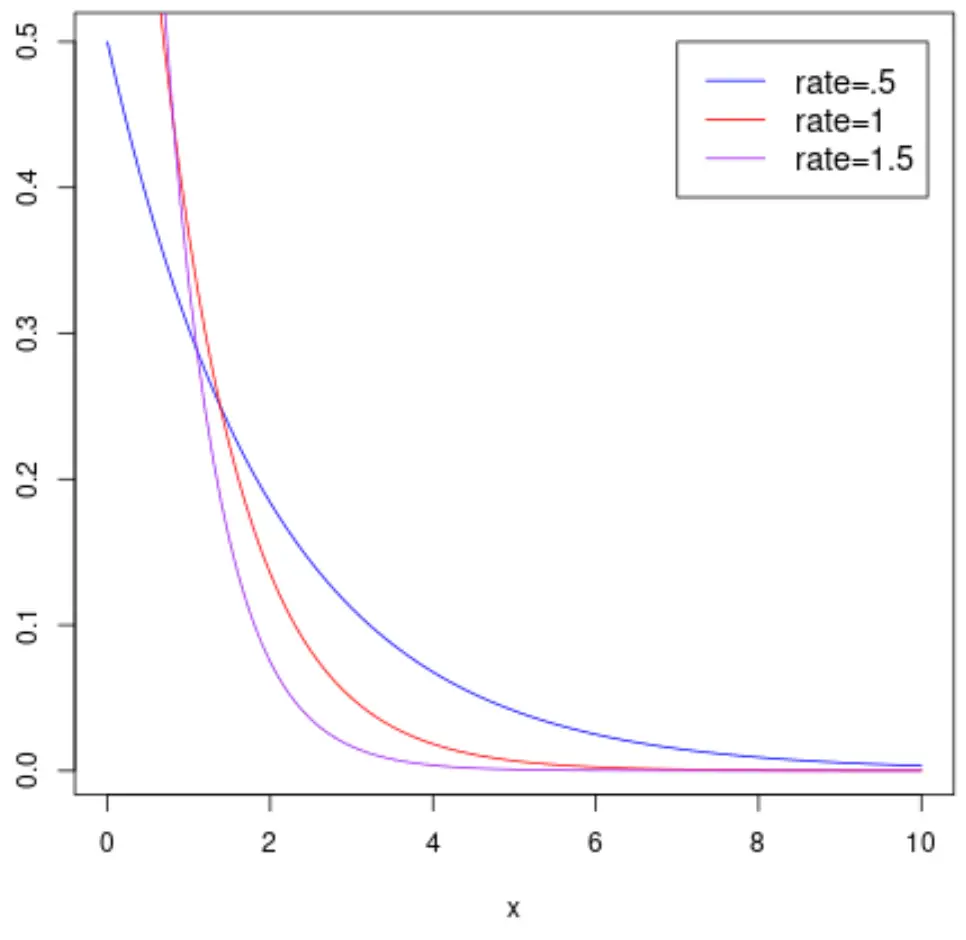
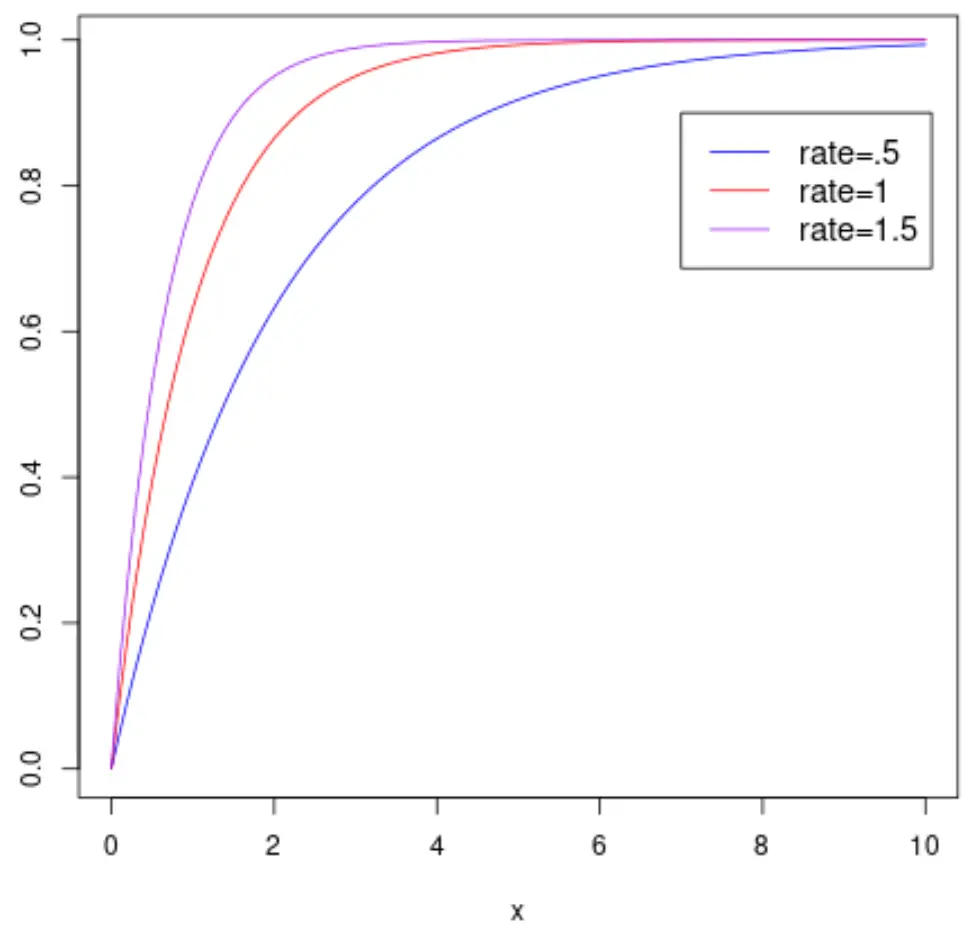
E o gráfico a seguir mostra a função de distribuição cumulativa de uma variável aleatória X que segue uma distribuição exponencial com diferentes parâmetros de taxa:

Nota: Confira este tutorial para aprender como traçar uma distribuição exponencial em R.

Propriedades da distribuição exponencial

A distribuição exponencial tem as seguintes propriedades:

• Média: 1/λ
• Diferença: 1 / λ ²

Por exemplo, suponha que o número médio de minutos entre as erupções de um determinado gêiser seja de 40 minutos. Calcularíamos a taxa como λ = 1/μ = 1/40 = 0,025.

Poderíamos então calcular as seguintes propriedades para esta distribuição:

• Tempo médio de espera para a próxima erupção: 1/λ = 1 /0,025 = 40
• Variação nos tempos de espera para a próxima erupção: 1/λ ² = 1 /.025 ² = 1600

Nota: A distribuição exponencial também possui uma propriedade sem memória , o que significa que a probabilidade de ocorrência de um evento futuro não é afetada pela ocorrência de eventos passados.

Problemas práticos de distribuição exponencial

Use os seguintes problemas práticos para testar seu conhecimento sobre distribuição exponencial.

Questão 1: Em média, um novo cliente entra numa loja a cada dois minutos. Após a chegada de um cliente, determine a probabilidade de um novo cliente chegar em menos de um minuto.

Solução 1: O tempo médio entre clientes é de dois minutos. Assim, a taxa pode ser calculada da seguinte forma:

• λ = 1/µ
• λ = 1/2
• λ = 0,5

Podemos inserir λ = 0,5 e x = 1 na fórmula CDF:

• P(X ≤ x) = 1 – e ^-λx
• P(X ≤ 1) = 1 – e ^-0,5(1)
• P(X ≤ 1) = 0,3935

A probabilidade de termos que esperar menos de um minuto pela chegada do próximo cliente é de 0,3935 .

Questão 2: Um terremoto ocorre em média a cada 400 dias em uma determinada região. Depois de um terremoto, determine a probabilidade de que passem mais de 500 dias antes que o próximo terremoto ocorra.

Solução 2: O tempo médio entre os terremotos é de 400 dias. Assim, a taxa pode ser calculada da seguinte forma:

• λ = 1/µ
• λ = 1/400
• λ = 0,0025

Podemos inserir λ = 0,0025 e x = 500 na fórmula CDF:

• P(X ≤ x) = 1 – e ^-λx
• P(X ≤ 1) = 1 – e ^-0,0025(500)
• P(X ≤ 1) = 0,7135

A probabilidade de termos que esperar menos de 500 dias pelo próximo terremoto é de 0,7135. Portanto, a probabilidade de termos de esperar mais de 500 dias pelo próximo terremoto é 1 – 0,7135 = 0,2865 .

Questão 3: Uma central de atendimento recebe em média uma nova chamada a cada 10 minutos. Depois que um cliente ligar, determine a probabilidade de um novo cliente ligar dentro de 10 a 15 minutos.

Solução 3: O tempo médio entre ligações é de 10 minutos. Assim, a taxa pode ser calculada da seguinte forma:

• λ = 1/µ
• λ = 1/10
• λ = 0,1

Podemos usar a seguinte fórmula para calcular a probabilidade de um novo cliente ligar dentro de 10 a 15 minutos:

• P(10 <X ≤ 15) = (1 – e ^-0,1(15) ) – (1 – e ^-0,1(10) )
• P(10 <X ≤ 15) = 0,7769 – 0,6321
• P(10 <X ≤ 15) = 0,1448

A probabilidade de um novo cliente ligar dentro de 10 a 15 minutos. é 0,1448 .

Recursos adicionais

Os tutoriais a seguir fornecem introduções a outras distribuições de probabilidade comuns.

Uma introdução à distribuição normal
Uma introdução à distribuição binomial
Uma introdução à distribuição de Poisson
Uma introdução à distribuição uniforme