Como usar distribuição exponencial no excel

A distribuição exponencial é uma distribuição de probabilidade usada para modelar o tempo que temos que esperar até que um determinado evento ocorra.

Esta distribuição pode ser usada para responder perguntas como:

• Quanto tempo um varejista deve esperar que um cliente entre em sua loja?
• Por quanto tempo uma bateria continuará funcionando antes de morrer?
• Por quanto tempo um computador continuará funcionando antes de quebrar?

Em cada cenário, queremos calcular quanto tempo teremos que esperar até que determinado evento ocorra. Assim, cada cenário poderia ser modelado usando uma distribuição exponencial.

Se uma variável aleatória X segue uma distribuição exponencial, então a função de densidade cumulativa de X pode ser escrita:

F (x; λ) = 1 – e ^-λx

Ouro:

• λ: o parâmetro de taxa (calculado como λ = 1/μ)
• e: Uma constante aproximadamente igual a 2,718

Para calcular as probabilidades relacionadas à função densidade cumulativa da distribuição exponencial no Excel, podemos usar a seguinte fórmula:

 =EXPON.DIST(x, lambda, cumulative)

Ouro:

• x : o valor da variável aleatória distribuída exponencialmente
• lambda : o parâmetro de taxa
• cumulativo : se deve ou não usar a função de densidade cumulativa (VERDADEIRO ou FALSO)

Os exemplos a seguir mostram como usar esta fórmula na prática.

Exemplo 1: tempo até a chegada do próximo cliente

Um novo cliente entra em uma loja a cada dois minutos, em média. Após a chegada de um cliente, determine a probabilidade de um novo cliente chegar em menos de um minuto.

Solução: O tempo médio entre clientes é de dois minutos. Assim, a taxa pode ser calculada da seguinte forma:

• λ = 1/µ
• λ = 1/2
• λ = 0,5

Assim, podemos usar a seguinte fórmula no Excel para calcular a probabilidade de um novo cliente chegar em menos de um minuto:

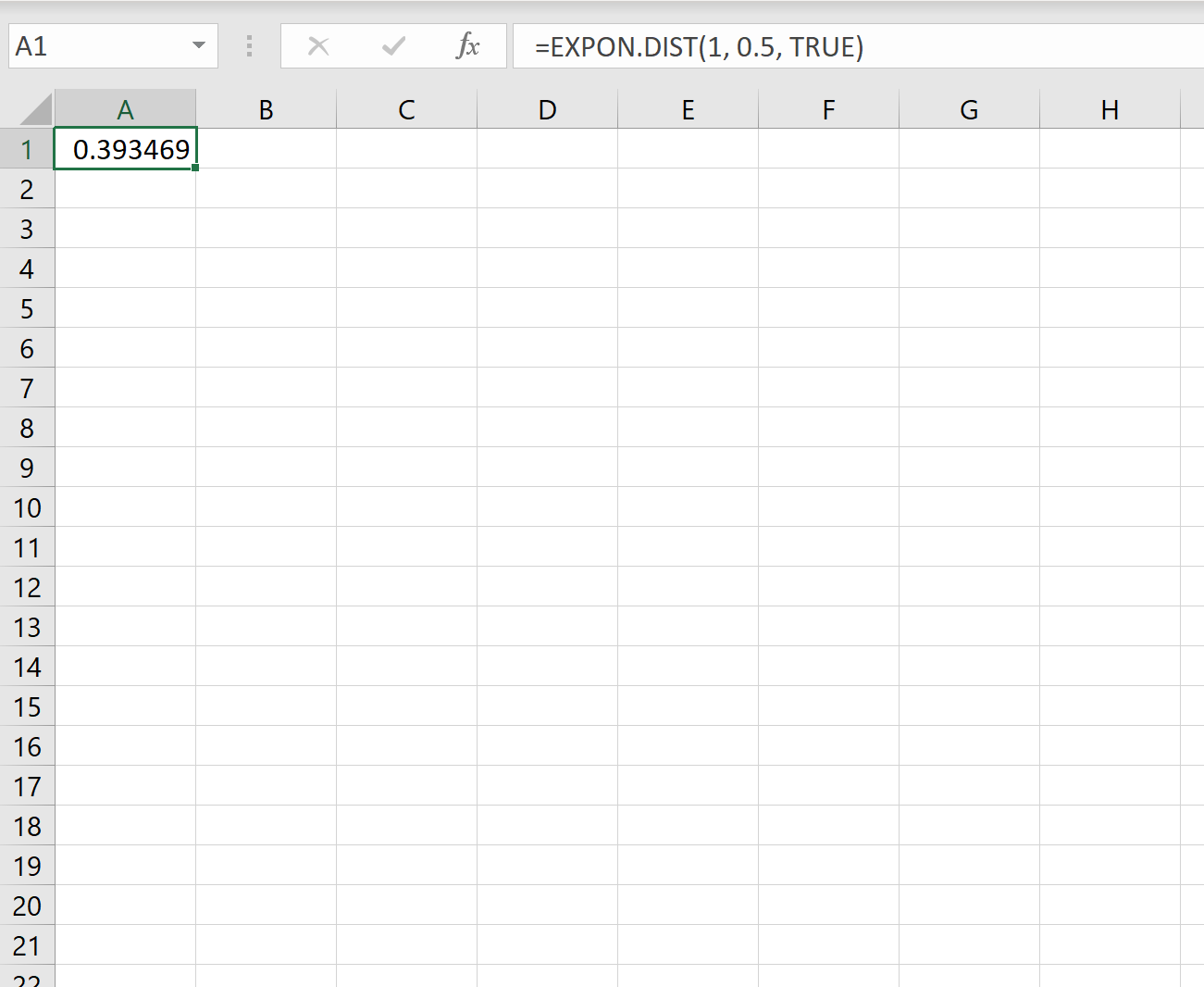
A probabilidade de termos que esperar menos de um minuto pela chegada do próximo cliente é 0,393469 .

Exemplo 2: Hora do próximo terremoto

Suponha que um terremoto ocorra em média a cada 400 dias em uma determinada região. Depois de um terremoto, determine a probabilidade de que passem mais de 500 dias antes que o próximo terremoto ocorra.

Solução: O tempo médio entre os terremotos é de 400 dias. Assim, a taxa pode ser calculada da seguinte forma:

• λ = 1/µ
• λ = 1/400
• λ = 0,0025

Portanto, podemos usar a seguinte fórmula no Excel para calcular a probabilidade de que o próximo terremoto demore menos de 500 dias para ocorrer:

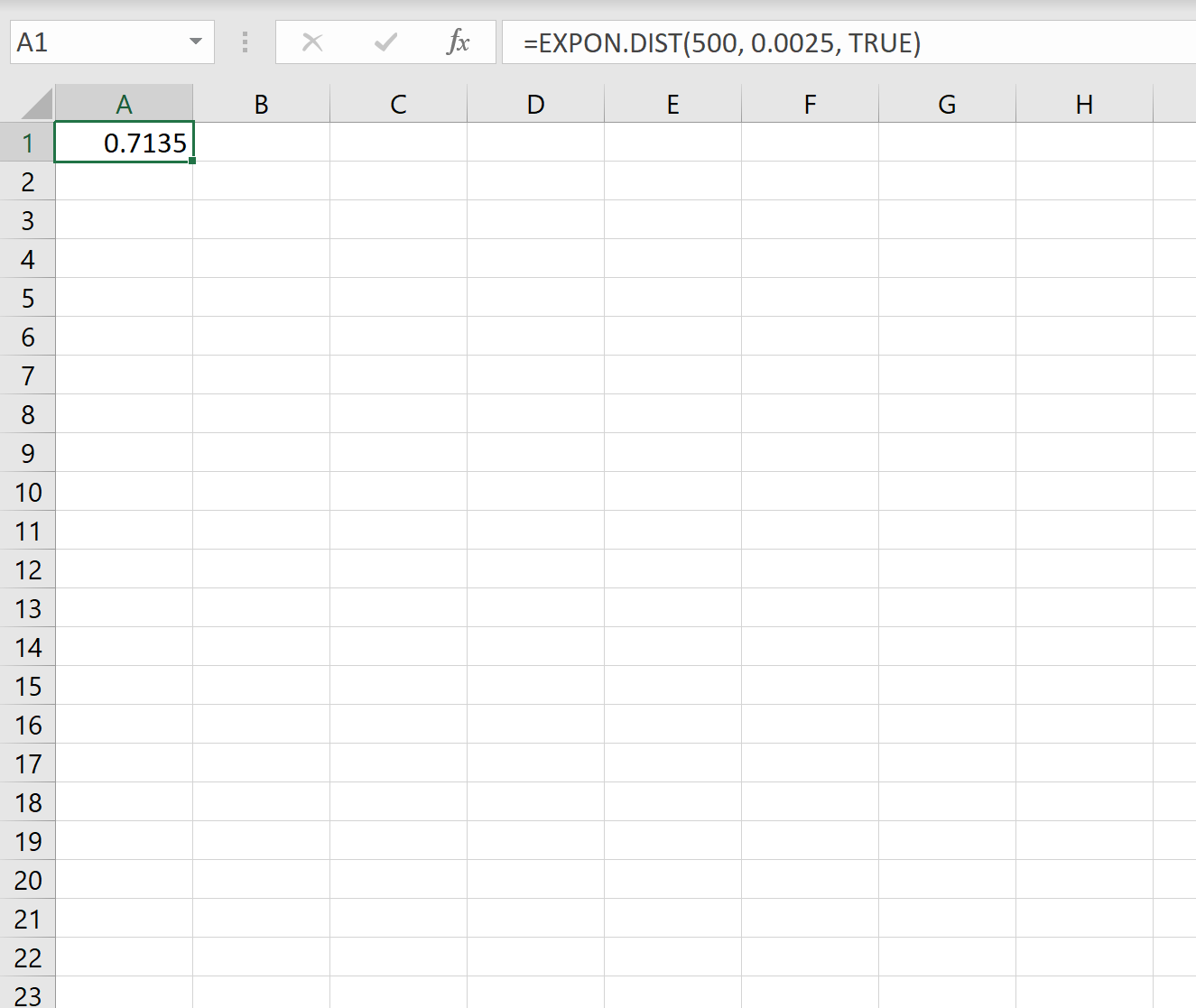
A probabilidade de faltar menos de 500 dias para o próximo terremoto é de 0,7135.

Portanto, a probabilidade de termos de esperar mais de 500 dias pelo próximo terremoto é 1 – 0,7135 = 0,2865 .

Exemplo 3: Tempo até a próxima ligação

Digamos que uma central de atendimento receba uma nova chamada a cada 10 minutos, em média. Depois que um cliente ligar, determine a probabilidade de um novo cliente ligar dentro de 10 a 15 minutos.

Solução: O tempo médio entre ligações é de 10 minutos. Assim, a taxa pode ser calculada da seguinte forma:

• λ = 1/µ
• λ = 1/10
• λ = 0,1

Portanto, podemos usar a seguinte fórmula no Excel para calcular a probabilidade de o próximo cliente ligar dentro de 10 a 15 minutos:

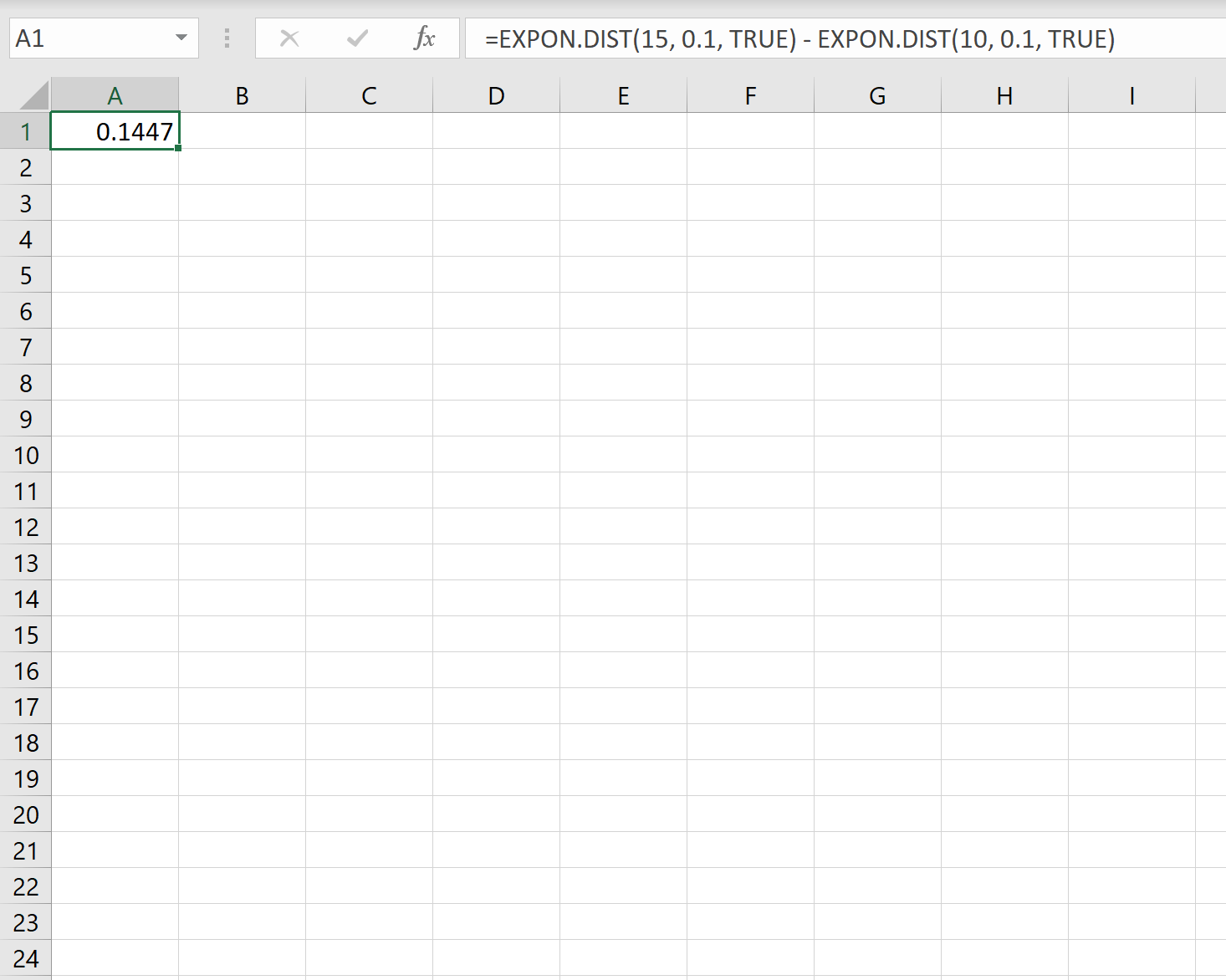
A probabilidade de um novo cliente ligar dentro de 10 a 15 minutos. é 0,1447 .

Recursos adicionais

Uma introdução à distribuição exponencial
A propriedade sem memória da distribuição exponencial
Como traçar uma distribuição exponencial em R