Uma introdução à distribuição geométrica

A distribuição geométrica descreve a probabilidade de ocorrer um certo número de falhas antes de ocorrer o primeiro sucesso em uma série de tentativas de Bernoulli.

Um ensaio de Bernoulli é uma experiência com apenas dois resultados possíveis – “sucesso” ou “fracasso” – e a probabilidade de sucesso é a mesma cada vez que a experiência é conduzida.

Um exemplo de ensaio de Bernoulli é o sorteio. A moeda só pode cair com duas caras (podemos chamar cara de “acerto” e coroa de “falha”) e a probabilidade de sucesso em cada lançamento é de 0,5, assumindo que a moeda é justa.

Se uma variável aleatória X segue uma distribuição geométrica, então a probabilidade de experimentar k falhas antes de experimentar o primeiro sucesso pode ser encontrada pela seguinte fórmula:

P(X=k) = (1-p) ^kp

Ouro:

• k: número de falhas antes do primeiro sucesso
• p: probabilidade de sucesso em cada tentativa

Por exemplo, digamos que queremos saber quantas vezes temos que jogar uma moeda honesta até dar cara. Podemos usar a fórmula acima para determinar a probabilidade de ocorrer 0, 1, 2, 3 falhas, etc. antes que a moeda caia em cara:

Nota: a moeda pode sofrer 0 “falha” se der cara no primeiro lançamento.

P(X=0) = (1-0,5) ⁰ (0,5) = 0,5

P(X=1) = (1-0,5) ¹ (0,5) = 0,25

P(X=2) = (1-0,5) ² (0,5) = 0,125

P(X=3) = (1-0,5) ³ (0,5) = 0,0625

Podemos calcular a probabilidade de qualquer número de lançamentos de moeda até o infinito. Em seguida, criamos um histograma simples para visualizar esta distribuição de probabilidade:

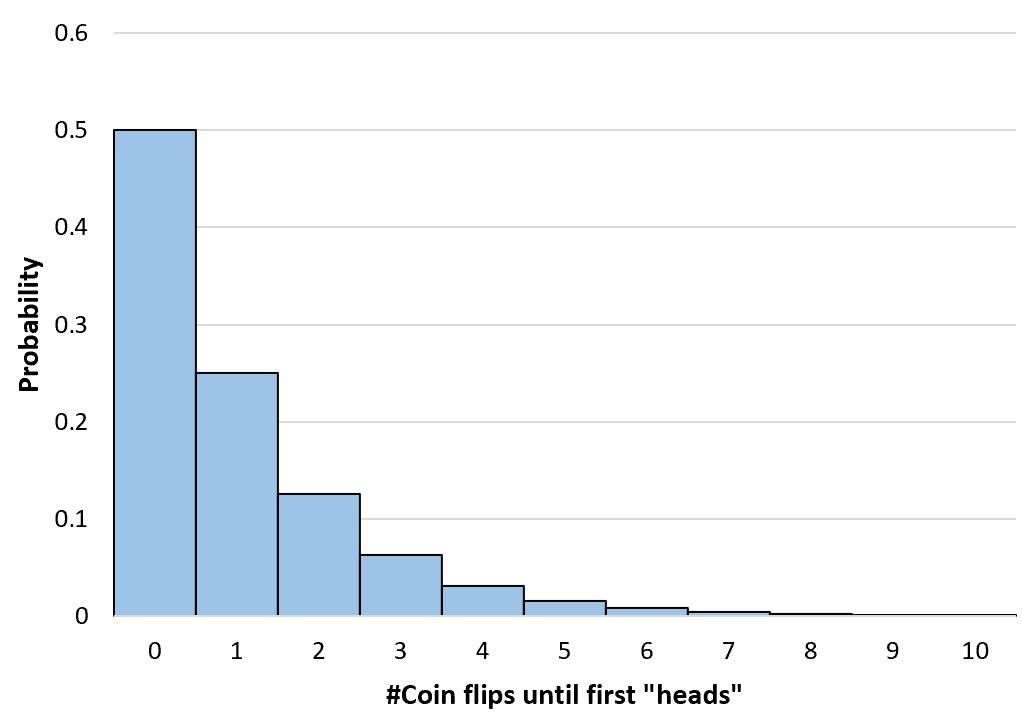
Cálculo de probabilidades geométricas cumulativas

A probabilidade cumulativa de experimentarmos k ou menos falhas até o primeiro sucesso pode ser encontrada pela seguinte fórmula:

P(X≤k) = 1 – (1-p) ^k+1

Ouro:

• k: número de falhas antes do primeiro sucesso
• p: probabilidade de sucesso em cada tentativa

Por exemplo, suponha que queiramos saber a probabilidade de serem necessárias três ou menos “erras” antes que a moeda finalmente dê cara. Usaríamos a seguinte fórmula para calcular essa probabilidade:

P(X≤3) = 1 – (1-0,5) ³⁺¹ = 0,9375

Podemos calcular cada probabilidade cumulativa usando uma fórmula semelhante:

P(X≤0) = 1 – (1-0,5) ⁰⁺¹ = 0,5

P(X≤1) = 1 – (1-0,5) ¹⁺¹ = 0,75

P(X≤2) = 1 – (1-0,5) ²⁺¹ = 0,875

Podemos calcular essas probabilidades cumulativas para qualquer número de lançamentos de moeda até o infinito. Podemos então criar um histograma para visualizar esta distribuição de probabilidade cumulativa:

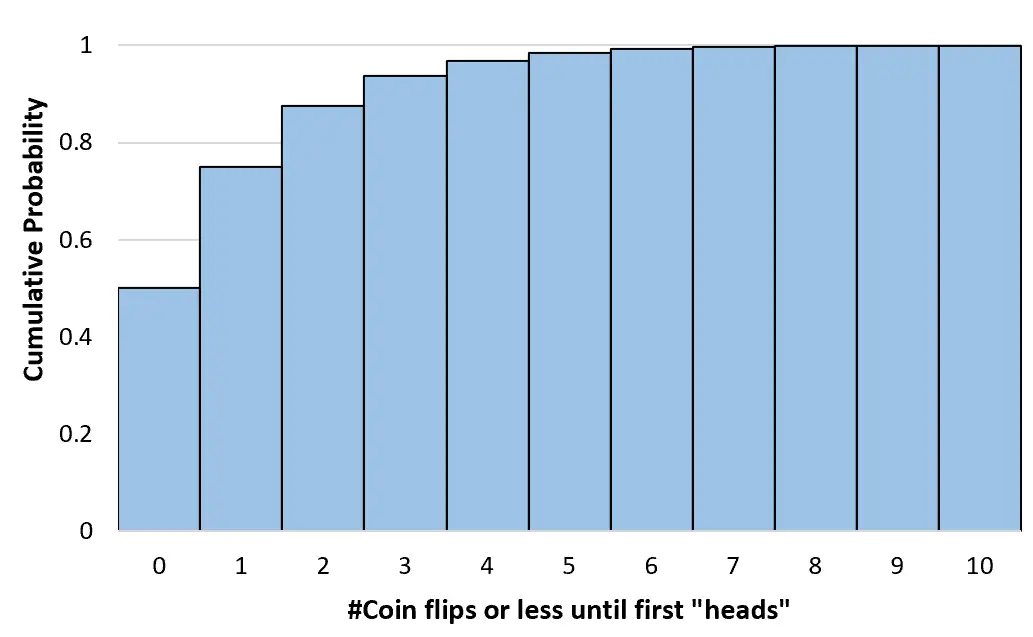
Propriedades da distribuição geométrica

A distribuição geométrica tem as seguintes propriedades:

A média da distribuição é (1-p) / p .

A variância da distribuição é (1-p) / p ² .

Por exemplo:

O número médio de vezes que esperamos que uma moeda caia cara antes de cair coroa seria (1-p) / p = (1-0,5) / 0,5 = 1 .

A variância do número de lançamentos até dar cara seria (1-p)/ ^p2 =(1-0,5)/. ⁵² = 2 .

Problemas práticos de distribuição geométrica

Use os seguintes problemas práticos para testar seu conhecimento sobre distribuição geométrica.

Observação: usaremos a Calculadora de Distribuição Geométrica para calcular as respostas a essas perguntas.

Problema 1

Pergunta: Um pesquisador espera do lado de fora de uma biblioteca para perguntar às pessoas se elas apoiam uma determinada lei. A probabilidade de uma determinada pessoa apoiar a lei é p = 0,2. Qual é a probabilidade de que a quarta pessoa com quem o pesquisador fala seja a primeira a apoiar a lei?

Resposta: O número de “fracassos” até o primeiro sucesso – ou seja, o número de pessoas que não apoiam a lei até que a primeira pessoa a apoie – é 3. Portanto, ao usar a calculadora de distribuição geométrica com p = 0,2 e x = 3 falhas, descobrimos que P(X=3) = 0,10240 .

Problema 2

Pergunta: Um pesquisador espera do lado de fora de uma biblioteca para perguntar às pessoas se elas apoiam uma determinada lei. A probabilidade de uma determinada pessoa apoiar a lei é p = 0,2. Qual é a probabilidade de o pesquisador ter que conversar com mais de quatro pessoas para encontrar alguém que apoie a lei?

Resposta: Usando a calculadora de distribuição geométrica com p =0,2 ex = 4 falhas, descobrimos que P(X>4) = 0,32768 .

Problema 3

Pergunta: Um pesquisador espera do lado de fora de uma biblioteca para perguntar às pessoas se elas apoiam uma determinada lei. A probabilidade de uma determinada pessoa apoiar a lei é p = 0,2. Qual é o número esperado de pessoas com quem a pesquisadora precisará conversar até encontrar alguém que apoie a lei?

Resposta: Lembre-se de que a média da distribuição geométrica é (1-p) / p . Nesta situação, a média seria (1-0,2) / 0,2 = 4 .