Como usar distribuição geométrica no excel

A distribuição geométrica descreve a probabilidade de ocorrer um certo número de falhas antes de ocorrer o primeiro sucesso em uma série de tentativas de Bernoulli.

Um ensaio de Bernoulli é uma experiência com apenas dois resultados possíveis – “sucesso” ou “fracasso” – e a probabilidade de sucesso é a mesma cada vez que a experiência é conduzida.

Um exemplo de ensaio de Bernoulli é o sorteio. A moeda só pode cair com duas caras (podemos chamar cara de “acerto” e coroa de “falha”) e a probabilidade de sucesso em cada lançamento é de 0,5, assumindo que a moeda é justa.

Se uma variável aleatória X segue uma distribuição geométrica, então a probabilidade de experimentar k falhas antes de experimentar o primeiro sucesso pode ser encontrada pela seguinte fórmula:

P(X=k) = (1-p) ^kp

Ouro:

• k: número de falhas antes do primeiro sucesso
• p: probabilidade de sucesso em cada tentativa

Os exemplos a seguir mostram como calcular probabilidades relacionadas à distribuição geométrica no Excel.

Exemplo 1: jogue uma moeda

Suponha que lançamos uma moeda e queremos saber a probabilidade de que sejam necessárias exatamente três “erras” antes que a moeda finalmente dê cara.

Usaríamos a seguinte fórmula para calcular essa probabilidade:

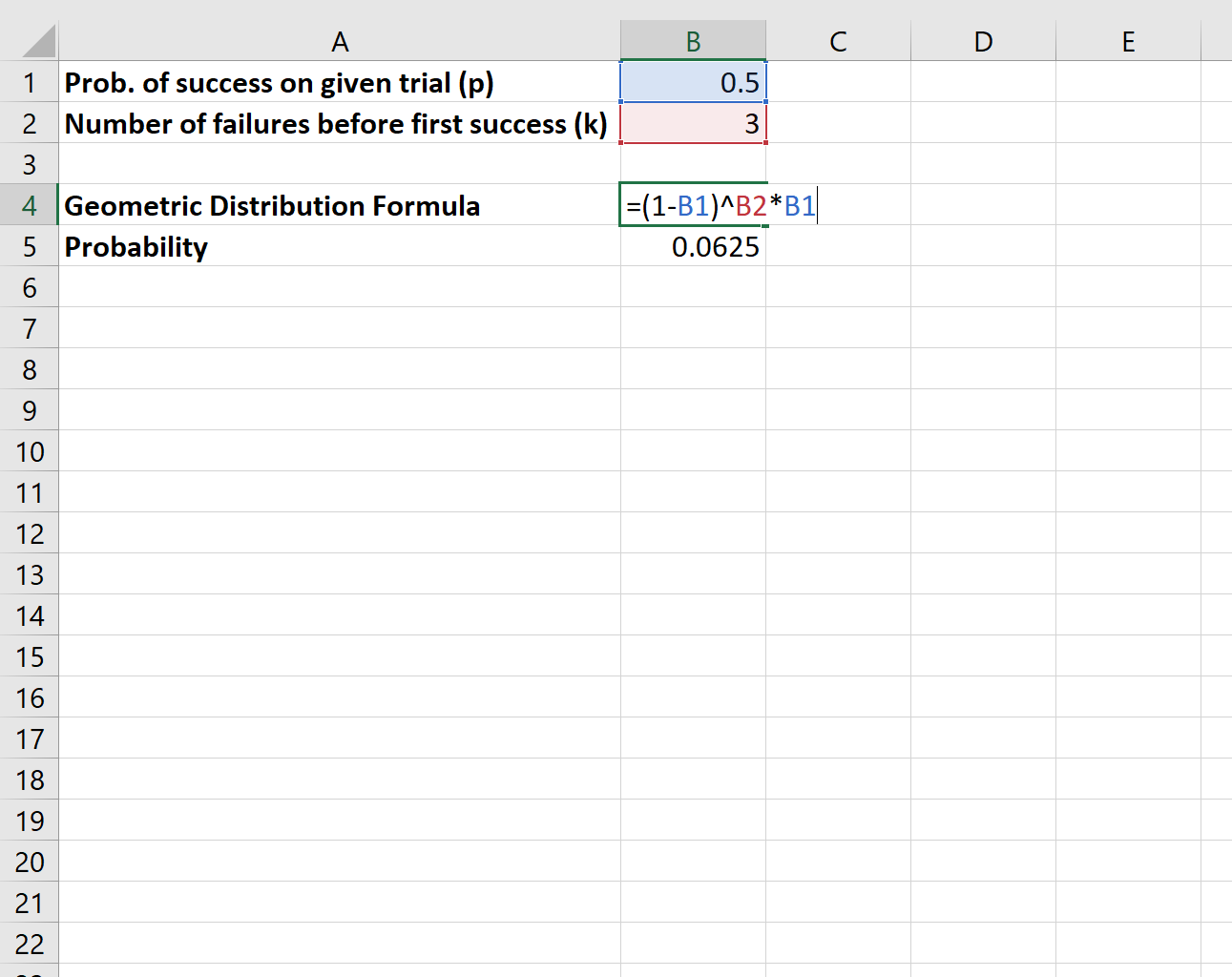
A probabilidade de experimentarmos três “erros” até que uma moeda finalmente dê cara é 0,0625 .

Exemplo 2: arremesso de lance livre

Suponha que um certo jogador de basquete acerte 60% de seus lances livres. Qual é a probabilidade de o jogador errar quatro lances livres até finalmente acertar um?

Usaríamos a seguinte fórmula para calcular essa probabilidade:

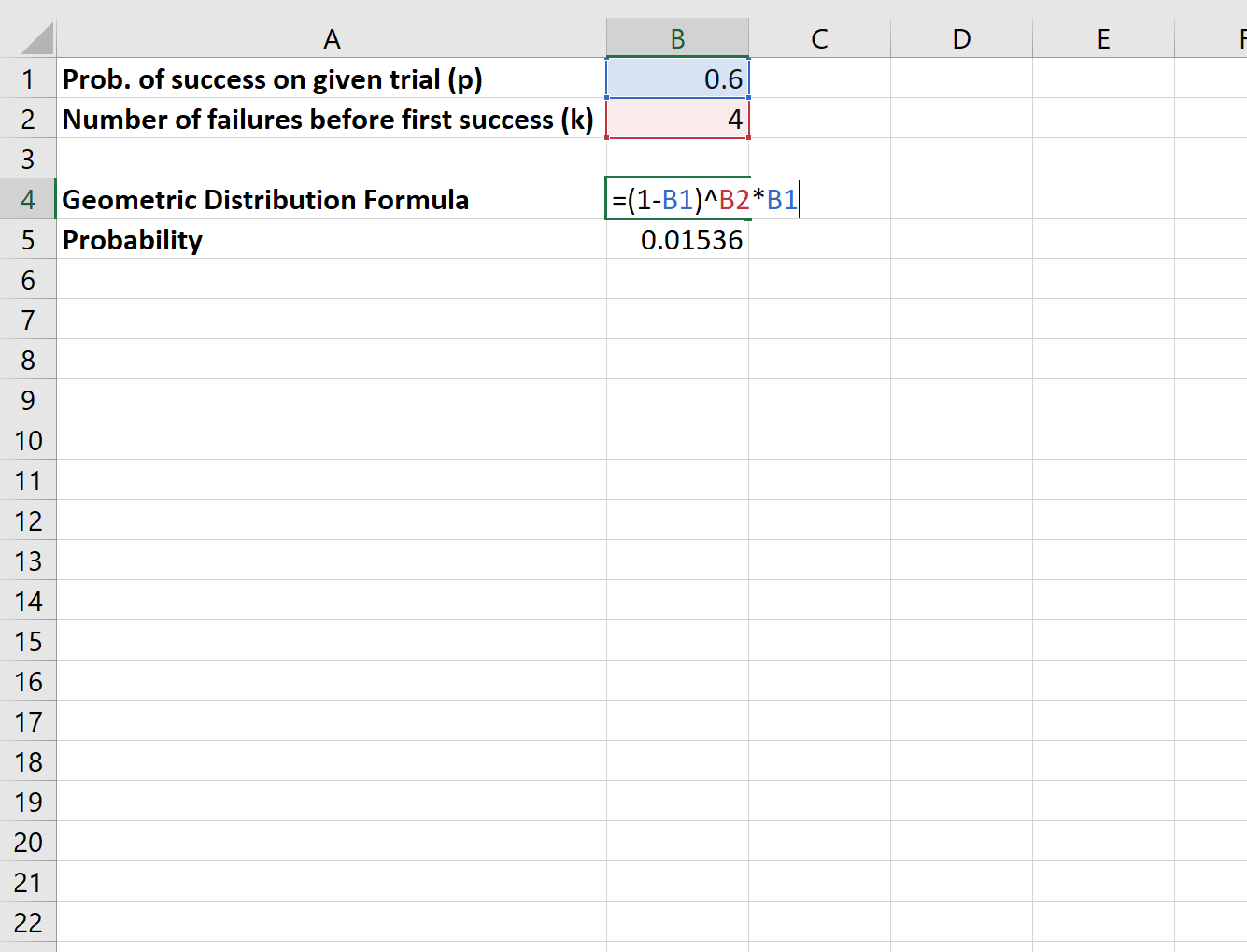
A probabilidade de o jogador errar quatro lances livres até finalmente acertar um é de 0,01536 .

Exemplo 3: Apoiando uma lei

Suponha que um pesquisador espere do lado de fora de uma biblioteca para perguntar às pessoas se elas apoiam uma determinada lei. A probabilidade de uma determinada pessoa apoiar a lei é p = 0,2. Qual é a probabilidade de que a quarta pessoa com quem o pesquisador fala seja a primeira a apoiar a lei?

Usaríamos a seguinte fórmula para calcular essa probabilidade:

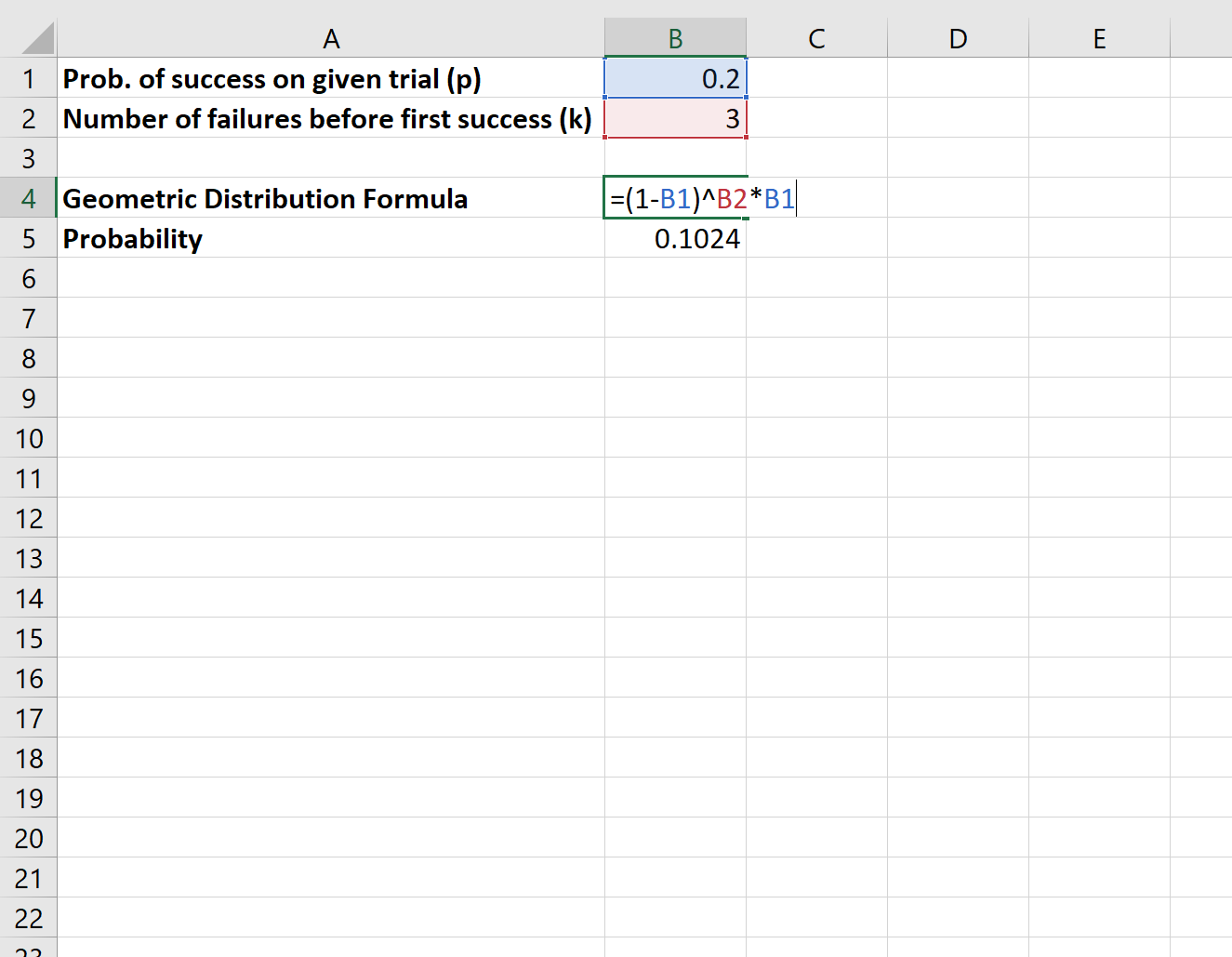
A probabilidade de a quarta pessoa com quem o pesquisador falar ser a primeira a apoiar a lei é de 0,1024 .

Recursos adicionais

Uma introdução à distribuição geométrica
Calculadora de distribuição geométrica
5 exemplos concretos de distribuição geométrica