O que é uma distribuição multimodal?

Uma distribuição multimodal é uma distribuição de probabilidade com dois ou mais modos.

Se você criar um histograma para visualizar uma distribuição multimodal, notará que ele possui vários picos:

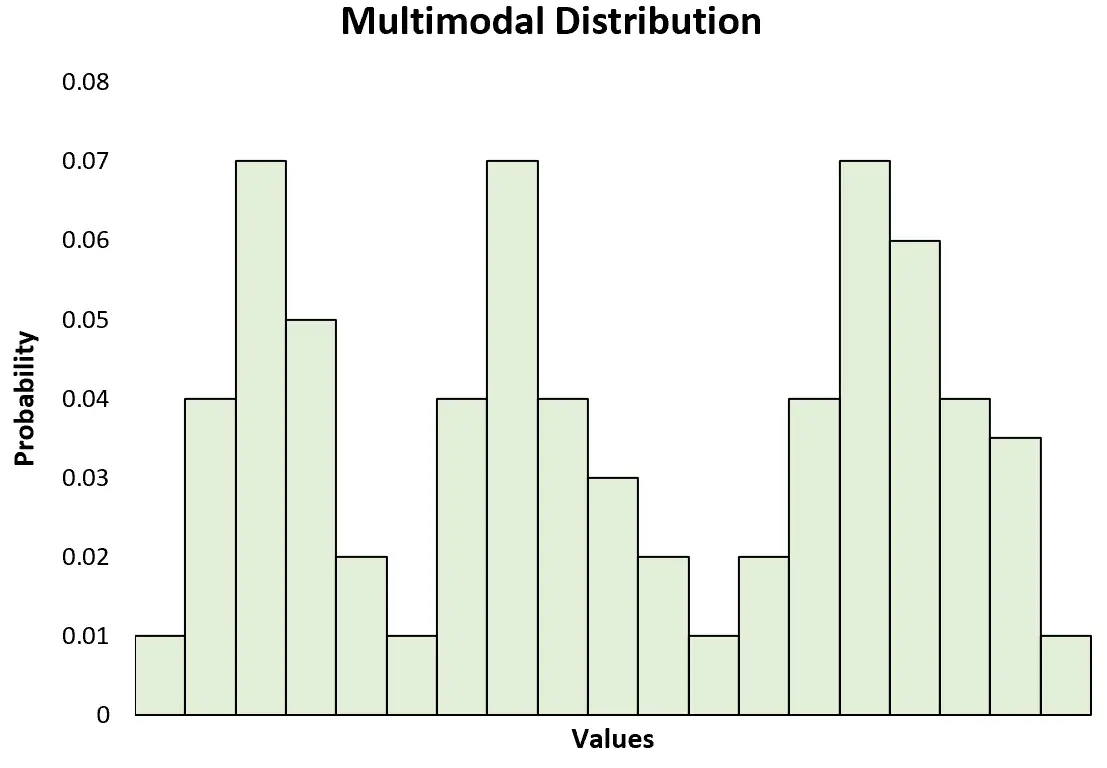
Se uma distribuição tiver exatamente dois picos, então é considerada uma distribuição bimodal , que é um tipo específico de distribuição multimodal.

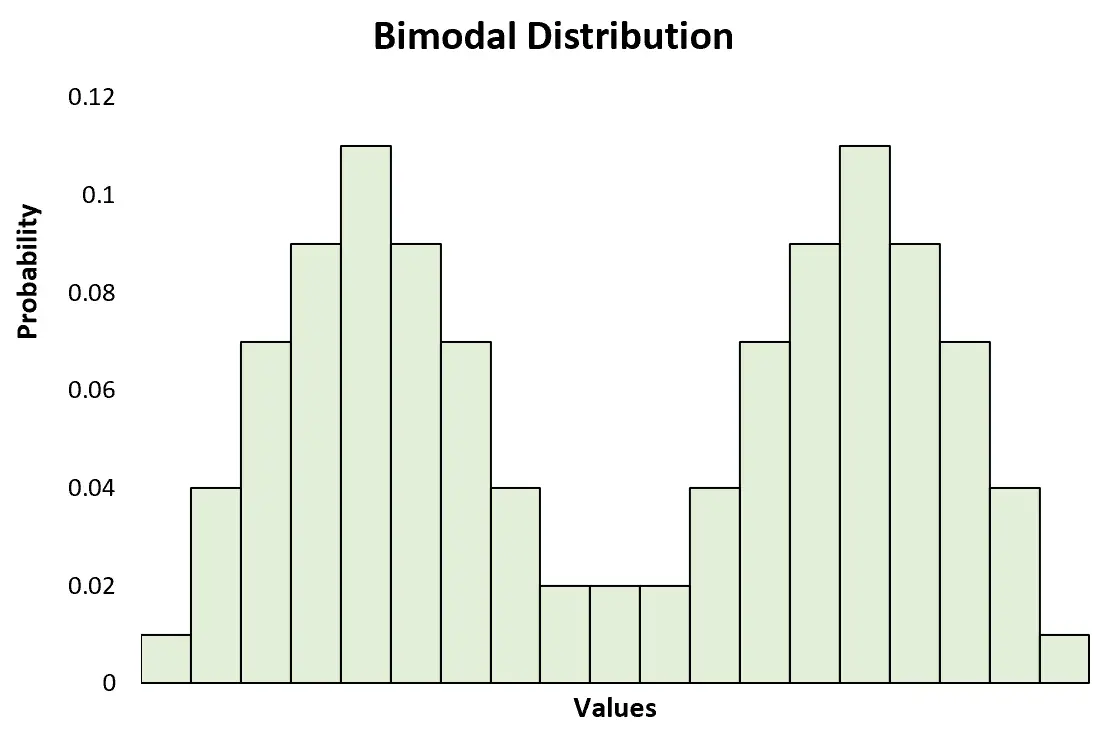
Isto contrasta com uma distribuição unimodal, que tem apenas um pico:

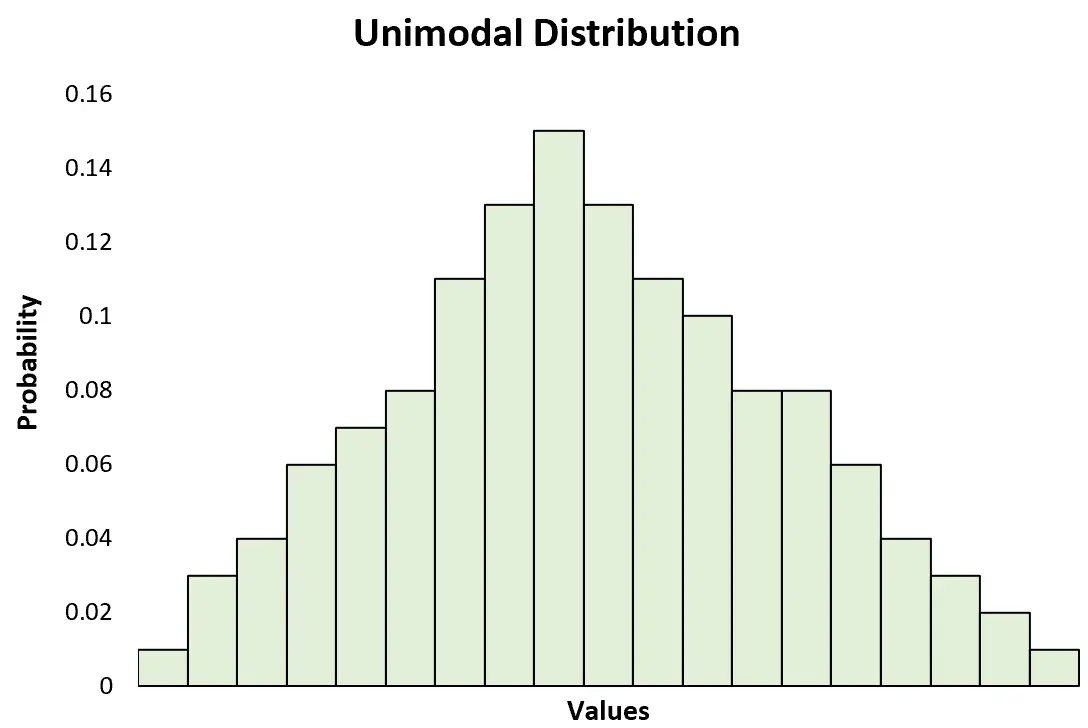
Embora as distribuições unimodais, como a distribuição normal , sejam mais frequentemente usadas para explicar tópicos em estatística, as distribuições multimodais aparecem com bastante frequência na prática, por isso é útil saber como reconhecê-las e analisá-las.

Exemplos de distribuições multimodais

Aqui estão alguns exemplos de distribuições multimodais.

Exemplo 1: Distribuição de resultados de exames

Suponha que um professor dê uma prova para sua turma. Alguns alunos estudaram, outros não. Quando o professor cria um histograma de notas de exames, ele segue uma distribuição multimodal com um pico em torno das notas baixas para os alunos que não estudaram e outro pico em torno das notas altas para os alunos que estudaram:

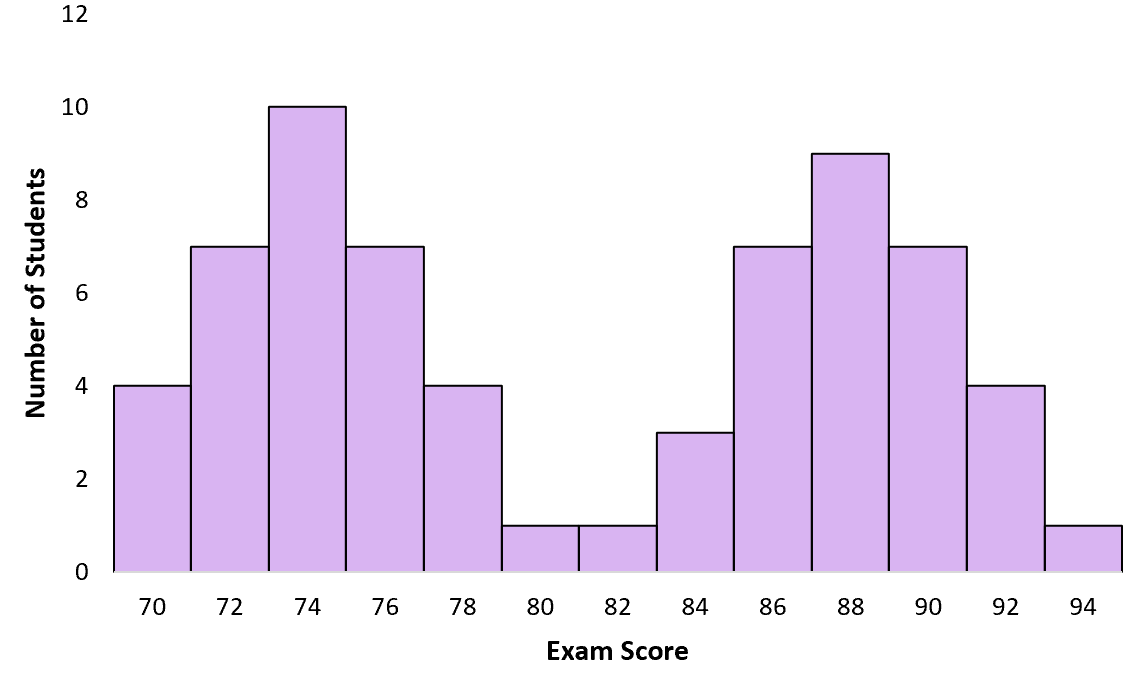
Exemplo 2: Altura de diferentes espécies de plantas

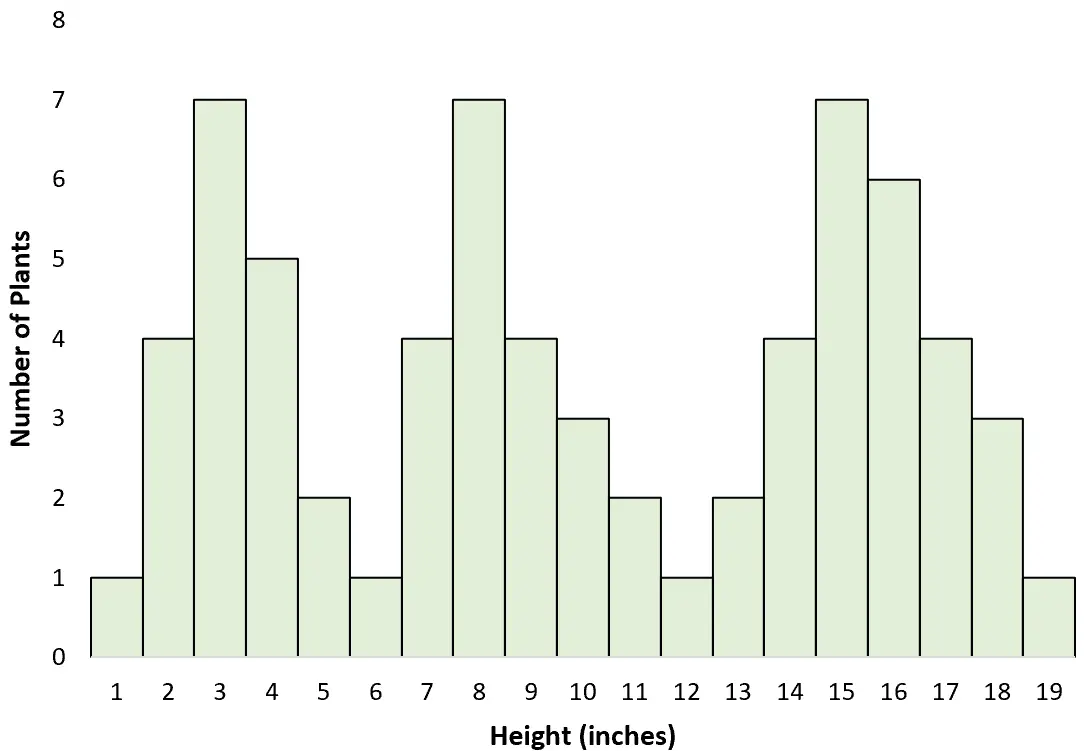
Suponha que um cientista caminhe por um campo e meça a altura de diferentes plantas. Sem perceber, ela mede o tamanho de três espécies diferentes: uma bem grande, outra de tamanho médio e outra bem pequena.

Ao criar um histograma para visualizar a distribuição de altura, ela descobre que é multimodal: cada pico representa a altura mais comum das três espécies diferentes.

Exemplo 3: Distribuição de clientes

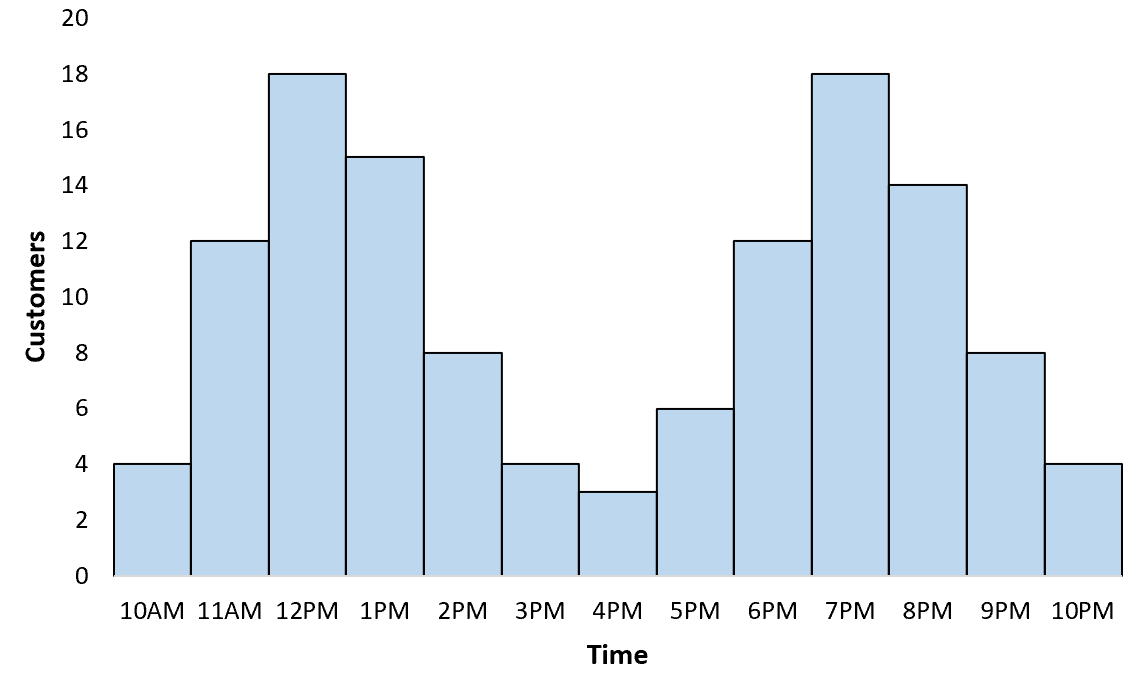
O proprietário de um restaurante monitora o número de clientes que o visitam a cada hora. Ao criar um histograma para visualizar a distribuição dos clientes, ele vê que a distribuição é multimodal: há um pico no horário do almoço e outro pico no horário do jantar.

Quais são as causas das distribuições multimodais?

Geralmente há uma de duas causas subjacentes às distribuições multimodais:

1. Vários grupos são agrupados.

Distribuições multimodais podem ocorrer quando você coleta dados de vários grupos sem perceber.

Por exemplo, se um cientista medir, sem saber, a altura de três espécies de plantas diferentes localizadas no mesmo campo, a distribuição de todas as plantas parecerá multimodal quando colocadas no mesmo histograma.

2. Existe um fenômeno subjacente.

Distribuições multimodais também podem ocorrer devido a certos fenômenos subjacentes.

Por exemplo, o número de clientes que visitam um restaurante a cada hora segue uma distribuição multimodal, uma vez que as pessoas tendem a comer nos restaurantes em dois horários distintos: almoço e jantar. Este comportamento humano subjacente é a origem da distribuição multimodal.

Como analisar distribuições multimodais

Freqüentemente descrevemos distribuições usando a média ou mediana porque isso nos dá uma ideia de onde está o “centro” da distribuição.

Infelizmente, não é útil saber a média e a mediana para uma distribuição bimodal. Por exemplo, a nota média do exame dos alunos no exemplo acima é 81:

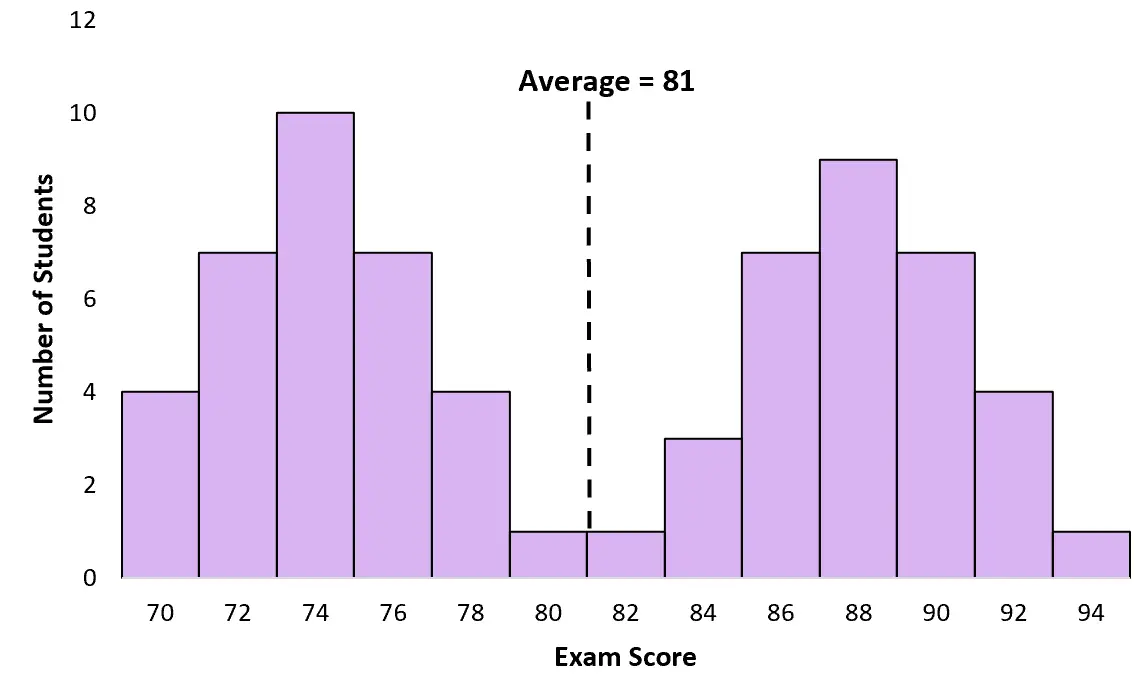
No entanto, muito poucos alunos obtiveram pontuações próximas de 81. Neste caso, a média é enganadora. A maioria dos alunos obteve pontuação em torno de 74 ou 88.

A melhor maneira de analisar e interpretar distribuições bimodais é simplesmente dividir os dados em dois grupos distintos e depois analisar a localização central e a distribuição de cada grupo individualmente.

Por exemplo, podemos dividir os resultados dos exames em “pontuações baixas” e “pontuações altas” e então encontrar a média e o desvio padrão para cada grupo.

Ao calcular estatísticas resumidas para uma determinada distribuição, como média, mediana ou desvio padrão, certifique-se de visualizar a distribuição para determinar se ela é unimodal ou multimodal.

Se uma distribuição for multimodal, pode ser enganoso descrevê-la usando uma única média, mediana ou desvio padrão.