Distribuição normal

By Dr. benjamim anderson Agosto 3, 2023 Probabilidade 0 Comments

Este artigo explica o que é a distribuição normal nas estatísticas. Assim, você encontrará a definição de distribuição normal, exemplos de distribuições normais e quais são as propriedades da distribuição normal.

Qual é a distribuição normal?

A distribuição normal é uma distribuição de probabilidade contínua cujo gráfico tem forma de sino e é simétrico em relação à sua média. Nas estatísticas, a distribuição normal é utilizada para modelar fenômenos com características muito diferentes, por isso essa distribuição é tão importante.

Na verdade, em estatística, a distribuição normal é considerada de longe a distribuição mais importante de todas as distribuições de probabilidade, porque não só pode modelar um grande número de fenómenos do mundo real, mas a distribuição normal também pode ser usada para aproximar outros tipos de fenómenos. distribuições. sob certas condições.

O símbolo da distribuição normal é a letra N maiúscula. Assim, para indicar que uma variável segue uma distribuição normal, ela é indicada pela letra N e os valores de sua média aritmética e desvio padrão são somados entre parênteses.

$X\sim N(\mu,\sigma)$

A distribuição normal tem muitos nomes diferentes, incluindo distribuição Gaussiana , distribuição Gaussiana e distribuição Laplace-Gauss .

Exemplos de distribuições normais

Normalmente, os conjuntos de dados que seguem uma distribuição normal contêm um grande número de observações e cobrem tópicos muito gerais. Abaixo estão vários exemplos de amostras estatísticas que geralmente podem ser modeladas com uma distribuição normal.

Exemplos de distribuição normal:

O tamanho dos alunos em um curso.
O QI dos trabalhadores de uma empresa.
O número de peças defeituosas produzidas em uma fábrica em um dia.
As notas obtidas em um exame pelos alunos de um curso.
A rentabilidade das ações das empresas listadas em bolsa.

Gráfico de distribuição normal

Depois de ver o que é a distribuição normal e alguns exemplos desse tipo de distribuição de probabilidade, vamos ver como é seu gráfico para entender melhor o conceito.

No gráfico a seguir você pode ver como a função densidade da distribuição normal varia dependendo dos valores de sua média aritmética e desvio padrão.

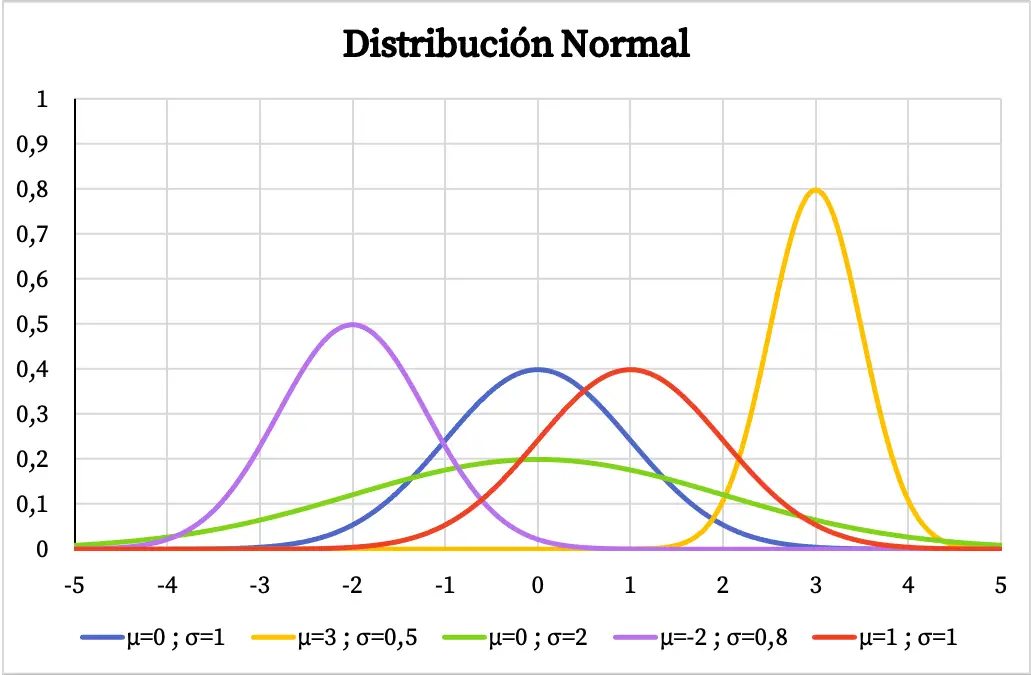
Tendo formato de sino centrado na média aritmética, se uma variável tem distribuição normal significa que o valor mais repetido é a média e que os valores em torno da média se repetem com mais frequência que os valores extremos. Da mesma forma, quanto maior o desvio padrão da distribuição normal, mais plana será a forma da sua representação gráfica.

Por outro lado, o gráfico da função de probabilidade cumulativa da distribuição normal também depende dos valores de sua média aritmética e desvio padrão, como você pode ver na imagem a seguir:

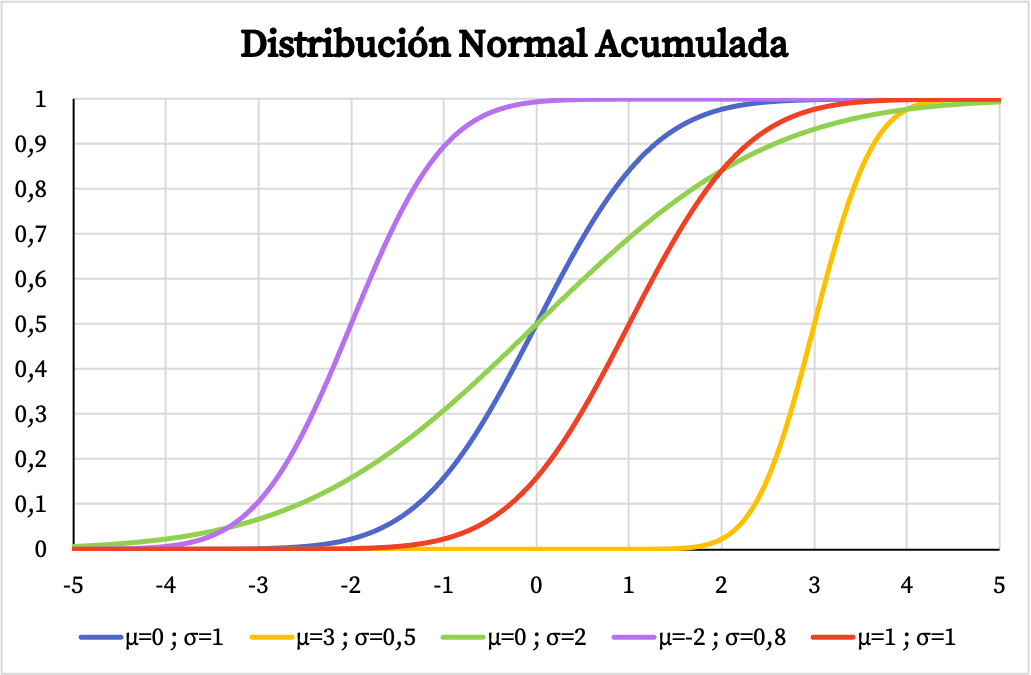
A função densidade e a função distribuição da distribuição normal permitem calcular probabilidades ligadas a esta distribuição. No entanto, em vez de usar suas fórmulas, você pode usar diretamente as tabelas de distribuição normais porque é mais rápido. Você pode consultar essas tabelas no seguinte link:

➤ Veja: Tabela de distribuição normal

Características da distribuição normal

A distribuição normal tem as seguintes características:

A distribuição normal depende de dois parâmetros característicos, que são a sua média aritmética (μ) e o seu desvio padrão (σ).

$X\sim N(\mu,\sigma)$

A distribuição normal pode assumir valores positivos e negativos, portanto o domínio da distribuição normal consiste em números reais.

$x\in \mathbb{R}$

A mediana e a moda da distribuição normal são iguais à média aritmética da distribuição.

$Me=Mo=\mu$

O coeficiente de assimetria e o coeficiente de curtose da distribuição normal são zero.

$\begin{array}{c}A=0\\[2ex]C=0\end{array}$

A fórmula para a função densidade da distribuição normal é:

$\displaystyle P[X=x]=\frac1{\sigma\sqrt{2\pi}}\; e^{ - \frac{(x-\mu)^2}{2\sigma^2}}$

Da mesma forma, a fórmula para a função de probabilidade cumulativa da distribuição normal é:

$\displaystyle P[X\leq x]=\frac{1}{\sigma\sqrt{2\pi}}\int_{-\infty}^x e^{-\frac{(x - \mu)^2}{2\sigma^2}}\, dx ,\quad x\in\mathbb{R}$

Uma aplicação do teorema do limite central é que uma distribuição de Poisson pode aproximar-se de uma distribuição normal quando o valor de λ é suficientemente grande.

$\text{Poisson}(\lambda)\ \color{orange}\bm{\longrightarrow}\color{black} \ N\left(\lambda, \sqrt{\lambda}\right)$

Outra aplicação do teorema do limite central é que uma distribuição binomial pode ser aproximada por uma distribuição normal para conjuntos de dados com um grande número de observações.

$\text{Bin}(n,p)\ \color{orange}\bm{\longrightarrow}\color{black} \ N\left(n\cdot p, \sqrt{n\cdot p \cdot (1-p)}\right)$

Distribuição normal padrão

A distribuição normal padrão , também chamada de distribuição normal unitária , é o caso mais simples de distribuição normal. Mais precisamente, a distribuição normal padrão é uma distribuição normal com valores de média e desvio padrão iguais a 0 e 1 respectivamente.

$\displaystyle N(0,1) \ \color{orange}\bm{\longrightarrow}\color{black}\begin{cases} \mu=0\\[2ex]\sigma=1\end{cases}$

Observe que qualquer distribuição normal pode ser transformada em uma distribuição normal padrão aplicando um processo denominado digitação, que envolve subtrair sua média aritmética de cada valor e depois dividir por seu desvio padrão.

Além disso, a distribuição normal padrão é usada para determinar qualquer probabilidade de uma distribuição normal usando sua tabela de probabilidades. Assim, para encontrar a probabilidade de uma distribuição normal, a variável é primeiro inserida para convertê-la em uma distribuição normal padrão e, a seguir, olhamos na tabela para ver qual é o valor de probabilidade correspondente. Para saber mais, clique no seguinte link:

➤ Veja: Distribuição Normal Padrão

A distribuição normal e a regra empírica

Nas estatísticas, a regra prática , também chamada de regra 68-95-99,7 , é uma regra que define a porcentagem de valores em uma distribuição normal que estão dentro de três desvios padrão da média.

Mais especificamente, a regra prática afirma o seguinte:

68% dos valores em uma distribuição normal estão dentro de um desvio padrão da média.
95% dos valores em uma distribuição normal estão dentro de dois desvios padrão da média.
99,7% dos valores em uma distribuição normal estão dentro de três desvios padrão da média.

About Author

Dr. benjamim anderson

Olá, sou Benjamin, um professor aposentado de estatística que se tornou professor dedicado na Statorials. Com vasta experiência e conhecimento na área de estatística, estou empenhado em compartilhar meu conhecimento para capacitar os alunos por meio de Statorials. Saber mais