Como simular e traçar uma distribuição normal bivariada em r
Nas estatísticas, duas variáveis seguem uma distribuição normal bivariada se tiverem uma distribuição normal quando somadas.
Este tutorial explica como executar as seguintes tarefas em R:
- Simular uma distribuição normal bivariada
- Trace uma distribuição normal bivariada usando um gráfico de contorno (gráfico 2D)
- Trace uma distribuição normal bivariada usando um gráfico de superfície (gráfico 3D)
Vamos!
Exemplo 1: Simule uma distribuição normal bivariada em R
A maneira mais simples de simular uma distribuição normal bivariada em R é usar a função mvrnorm() do pacote MASS .
O código a seguir mostra como usar esta função para simular uma distribuição normal bivariada na prática:
library (MASS)
#make this example reproducible
set. seed ( 0 )
#simulate bivariate normal distribution
bivariate_data <- as. data . frame (mvrnorm(n= 100 ,
mu=c(0, 0),
Sigma=matrix(c(5, 3, 4, 4), ncol= 2 )))
#view first six rows of bivariate dataset
head(bivariate_data)
V1 V2
1 -2.03600343 -2.9623059
2 0.07719131 1.2948982
3 -3.26729701 -1.7928069
4 -2.62985132 -2.3015471
5 -1.75126215 0.3056698
6 3.67698436 2.2020238
Aqui está o que cada argumento da função mvrnorm() faz:
- n : Define o tamanho da amostra
- mu : Define a média de cada variável
- Sigma : Define a matriz de covariância das duas variáveis
O resultado final é um quadro de dados com duas variáveis que segue uma distribuição normal quando somadas.
Exemplo 2: traçando uma distribuição normal bivariada
A maneira mais fácil de traçar uma distribuição normal bivariada em R é usar as funções do pacote mnormt() .
Por exemplo, podemos usar a função contorno() deste pacote para criar um gráfico de contorno, que fornece uma visualização 2D da distribuição normal bivariada:
library (mnormt)
#make this example reproducible
set. seed ( 0 )
#create bivariate normal distribution
x <- seq(-3, 3, 0.1)
y <- seq(-3, 3, 0.1)
mu <- c(0, 0)
sigma <- matrix(c(2, -1, -1, 2), nrow= 2 )
f <- function(x, y) dmnorm(cbind(x, y), mu, sigma)
z <- outer(x, y, f)
#create contour plot
contour(x, y, z)
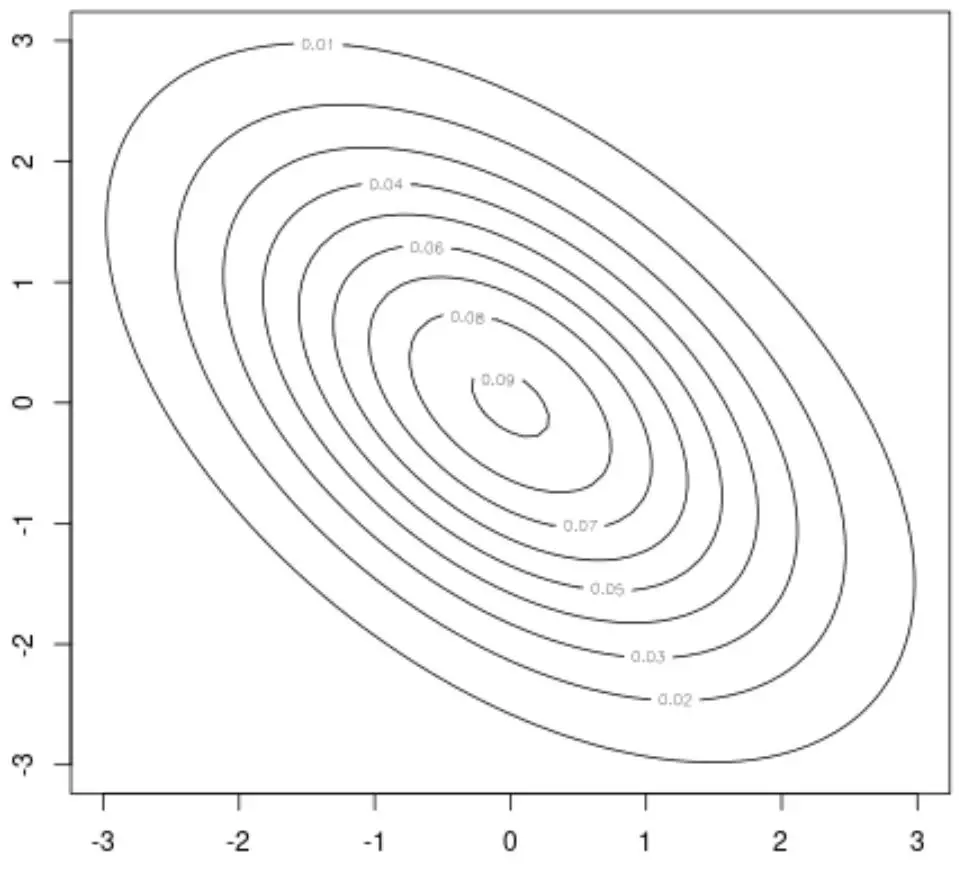
Também podemos usar a função persp() para criar um gráfico de superfície, que fornece uma visualização 3D da distribuição normal bivariada:
library (mnormt)
#make this example reproducible
set. seed ( 0 )
#create bivariate normal distribution
x <- seq(-3, 3, 0.1)
y <- seq(-3, 3, 0.1)
mu <- c(0, 0)
sigma <- matrix(c(2, -1, -1, 2), nrow= 2 )
f <- function(x, y) dmnorm(cbind(x, y), mu, sigma)
z <- outer(x, y, f)
#create surface plot
persp(x, y, z, theta= -30 , phi= 25 , expand= 0.6 , ticktype=' detailed ')
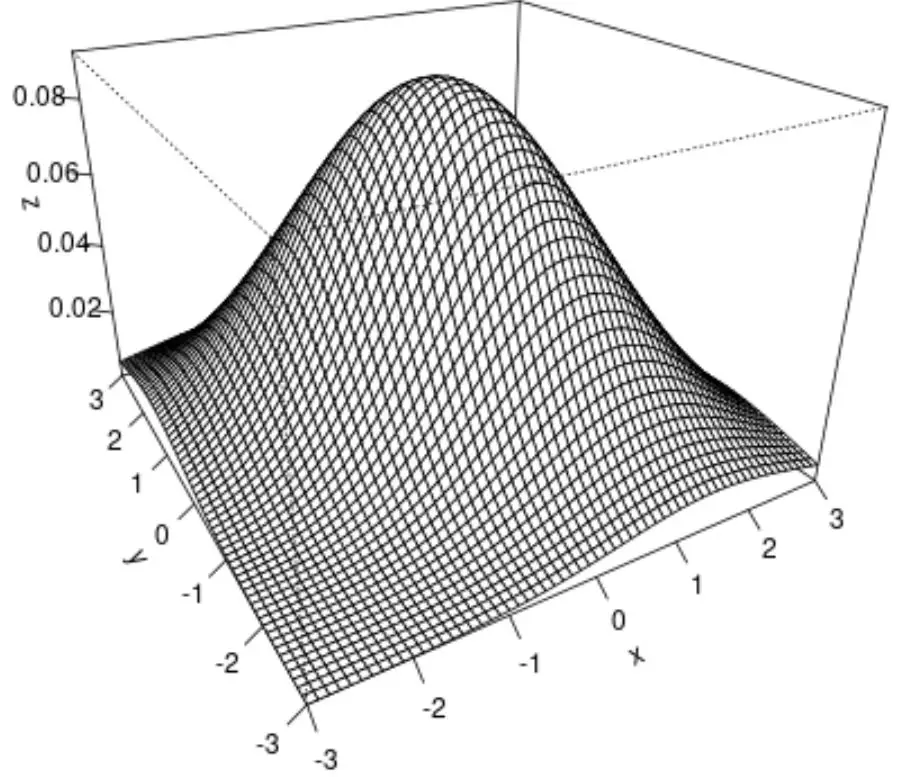
Aqui está o que cada argumento da função persp() faz:
- theta, phi : Define os ângulos de direção de visualização.
- expandir : controla o tamanho do eixo z.
- ticktype : Controla a aparência dos ticks nos eixos.
O resultado final é um gráfico de superfície 3D da distribuição normal bivariada.
Recursos adicionais
Os tutoriais a seguir explicam como usar outras distribuições de probabilidade em R:
Como usar a distribuição normal em R
Como usar distribuição binomial em R
Como usar a distribuição de Poisson em R
Como usar distribuição multinomial em R