Distribuição normal inversa: definição e exemplo
O termo distribuição normal inversa refere-se ao método de usar uma probabilidade conhecida para encontrar o valor crítico z correspondente em uma distribuição normal .
Isto não deve ser confundido com a distribuição gaussiana inversa , que é uma distribuição de probabilidade contínua.
Este tutorial fornece vários exemplos de uso da distribuição normal inversa em diferentes softwares estatísticos.
Distribuição normal inversa, temos calculadora TI-83 ou TI-84
É mais provável que você encontre o termo “distribuição normal inversa” em uma calculadora TI-83 ou TI-84, que usa a seguinte função para encontrar o valor z crítico que corresponde a uma certa probabilidade:
invNorm(probabilidade, μ, σ)
Ouro:
- probabilidade: o nível de significância
- μ: média populacional
- σ: desvio padrão populacional
Você pode acessar esta função em uma calculadora TI-84 pressionando 2nd e depois pressionando vars . Isso o levará a uma tela DISTR onde você poderá usar invNorm() :

Por exemplo, podemos usar esta função para encontrar o valor crítico z que corresponde a um valor de probabilidade de 0,05:
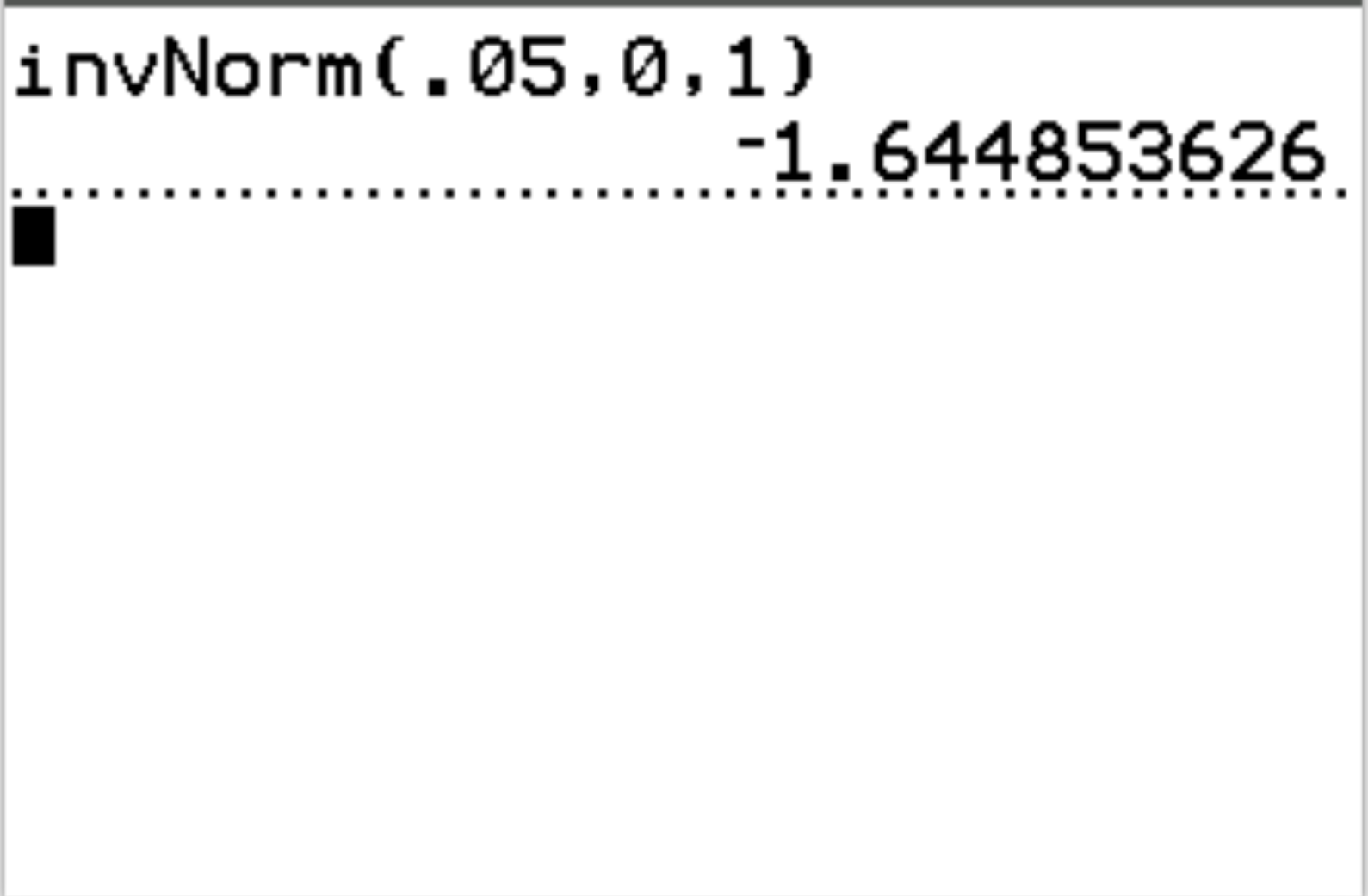
O valor z crítico que corresponde a um valor de probabilidade de 0,05 é -1,64485 .
Relacionado: Como usar invNorm em uma calculadora TI-84 (com exemplos)
Distribuição Normal Inversa no Excel
Para encontrar o valor crítico z associado a um determinado valor de probabilidade no Excel, podemos usar a função INVNORM() , que usa a seguinte sintaxe:
INVNORM(p, média, sd)
Ouro:
- p: o nível de significância
- média: média da população
- dp: desvio padrão populacional
Por exemplo, podemos usar esta função para encontrar o valor crítico z que corresponde a um valor de probabilidade de 0,05:
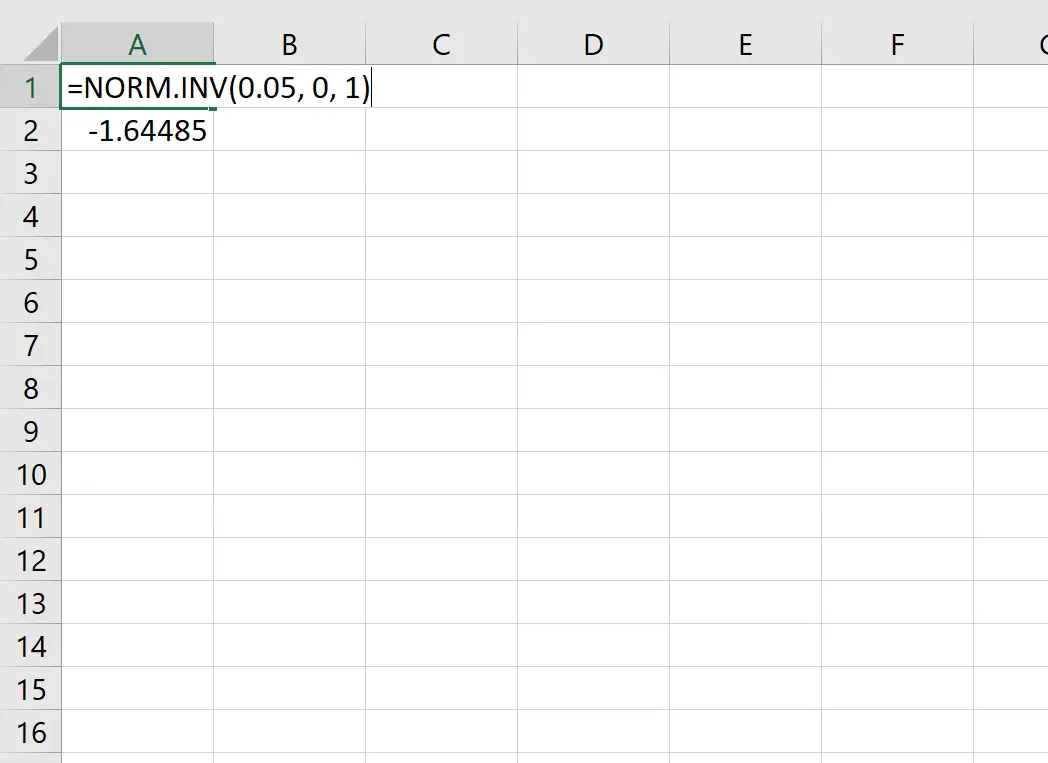
O valor z crítico que corresponde a um valor de probabilidade de 0,05 é -1,64485 .
Distribuição normal inversa em R
Para encontrar o valor crítico z associado a um determinado valor de probabilidade em R, podemos usar a função qnorm() , que usa a seguinte sintaxe:
qnorm (p, média, sd)
Ouro:
- p: o nível de significância
- média: média da população
- dp: desvio padrão populacional
Por exemplo, podemos usar esta função para encontrar o valor crítico z que corresponde a um valor de probabilidade de 0,05:
qnorm (p= .05 , mean= 0 , sd= 1 ) [1] -1.644854
Novamente, o valor z crítico que corresponde a um valor de probabilidade de 0,05 é -1,64485 .