Distribuição normal e distribuição normal padrão: a diferença

A distribuição normal é a distribuição de probabilidade mais comumente usada em estatísticas.

Possui as seguintes propriedades:

• Simétrico
• Em forma de sino
• A média e a mediana são iguais; ambos localizados no centro da distribuição

A média da distribuição normal determina a sua localização e o desvio padrão determina a sua propagação.

Por exemplo, o gráfico a seguir mostra três distribuições normais com diferentes médias e desvios padrão:

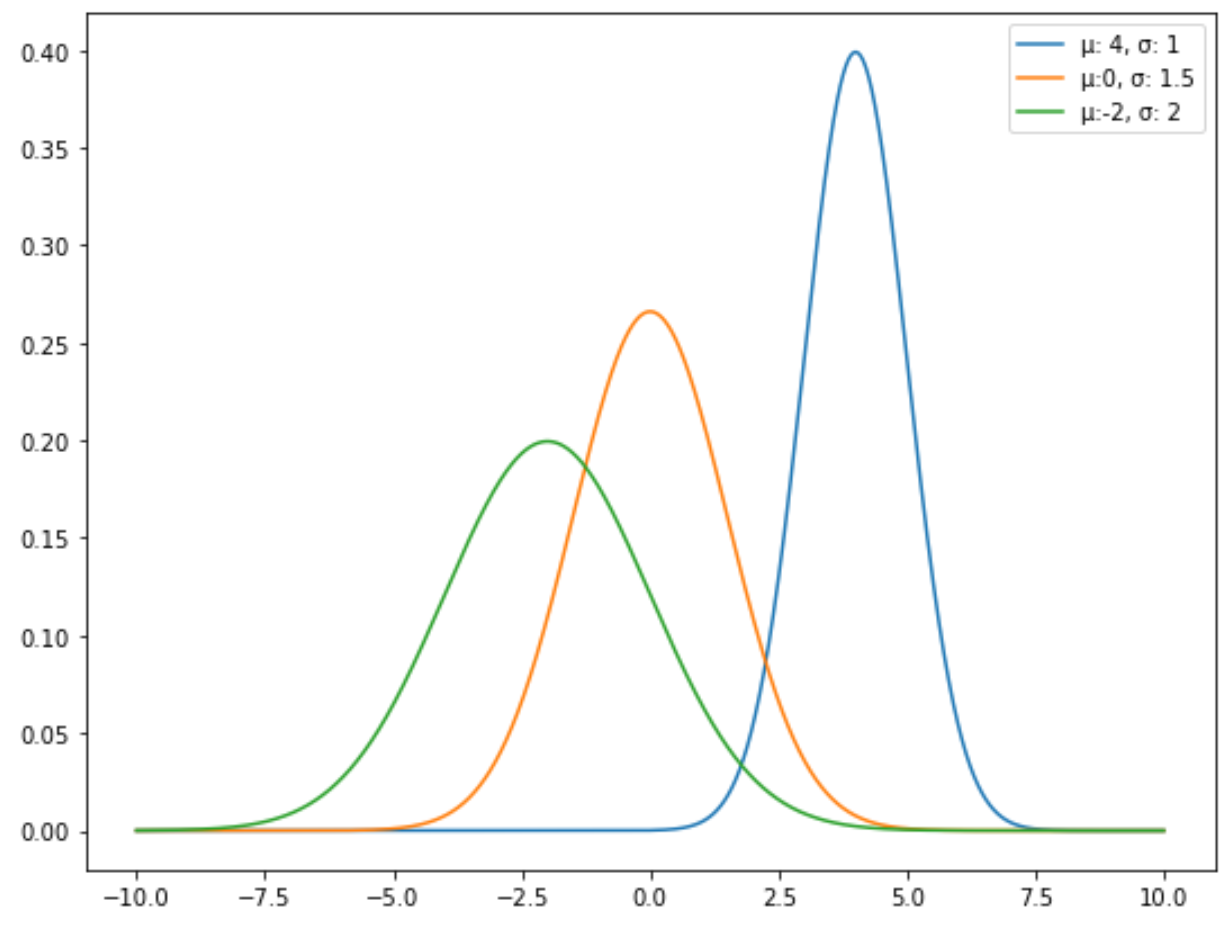
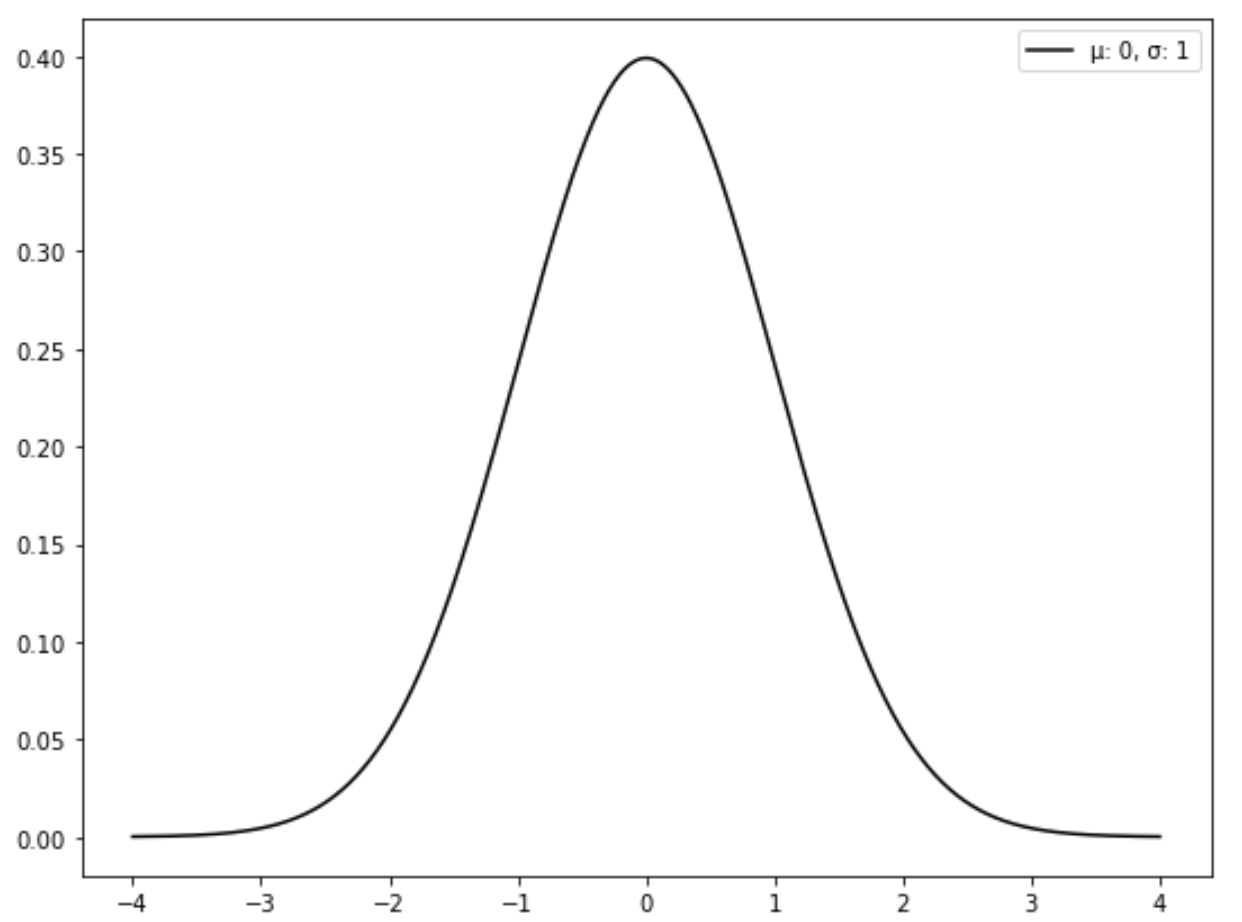
A distribuição normal padrão é um tipo específico de distribuição normal onde a média é 0 e o desvio padrão é 1.

O gráfico a seguir mostra uma distribuição normal padrão:

Como converter uma distribuição normal em uma distribuição normal padrão

Qualquer distribuição normal pode ser convertida em uma distribuição normal padrão convertendo os valores dos dados em escores z, usando a seguinte fórmula:

z = (x – μ) / σ

Ouro:

• x: valor dos dados individuais
• μ: Média da distribuição
• σ: Desvio padrão da distribuição

Por exemplo, suponha que temos o seguinte conjunto de dados com média 6 e desvio padrão de 2,152:

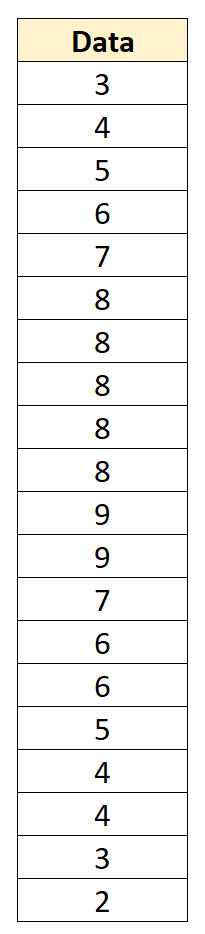
Podemos converter cada valor de dados individual em uma pontuação z subtraindo 6 de cada valor e dividindo por 2,152:

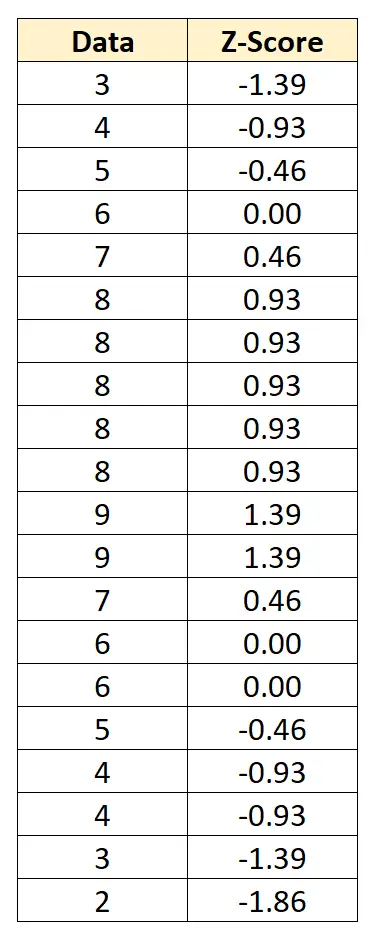
O escore z nos diz quantos desvios padrão cada ponto de dados está da média. Por exemplo, o primeiro valor de dados “3” está 1,39 desvios padrão abaixo da média.

A média dessa distribuição de pontuações tem média zero e desvio padrão de um.

Como usar a distribuição normal padrão

Uma distribuição normal padrão tem as seguintes propriedades:

• Cerca de 68% dos dados estão dentro de um desvio padrão da média
• Cerca de 95% dos dados estão dentro de dois desvios padrão da média.
• Cerca de 99,7% dos dados estão dentro de três desvios padrão da média.

Isso é conhecido como regra prática e é usado para entender a distribuição de valores em um conjunto de dados.

Por exemplo, suponha que a altura das plantas em um determinado jardim seja normalmente distribuída com média de 47,4 polegadas e desvio padrão de 2,4 polegadas.

Usando a regra prática, que porcentagem de plantas tem menos de 54,6 polegadas de altura?

A regra prática afirma que, para um determinado conjunto de dados com distribuição normal, 99,7% dos valores dos dados estão dentro de três desvios padrão da média. Isso significa que 49,85% dos valores ficam entre a média e três desvios padrão acima da média.

Neste exemplo, 54,6 está três desvios padrão acima da média. Como sabemos que 50% dos valores dos dados são menores que a média em uma distribuição normal, um total de 50% + 49,85% = 99,85% dos valores são menores que 54,6.

Portanto, 99,85% das plantas têm menos de 54,6 centímetros de altura.

Recursos adicionais

Problemas na prática de regras práticas
Calculadora de regras práticas
Como aplicar a regra prática no Excel