Distribuição normal e distribuição t: qual a diferença?
A distribuição normal é a distribuição mais comumente usada em todas as estatísticas e é conhecida por ser simétrica e em forma de sino.
Uma distribuição intimamente relacionada é a distribuição t , que também é simétrica e em forma de sino, mas tem “caudas” mais pesadas que a distribuição normal.
Em outras palavras, mais valores na distribuição estão localizados nas extremidades do que no centro em comparação com a distribuição normal:
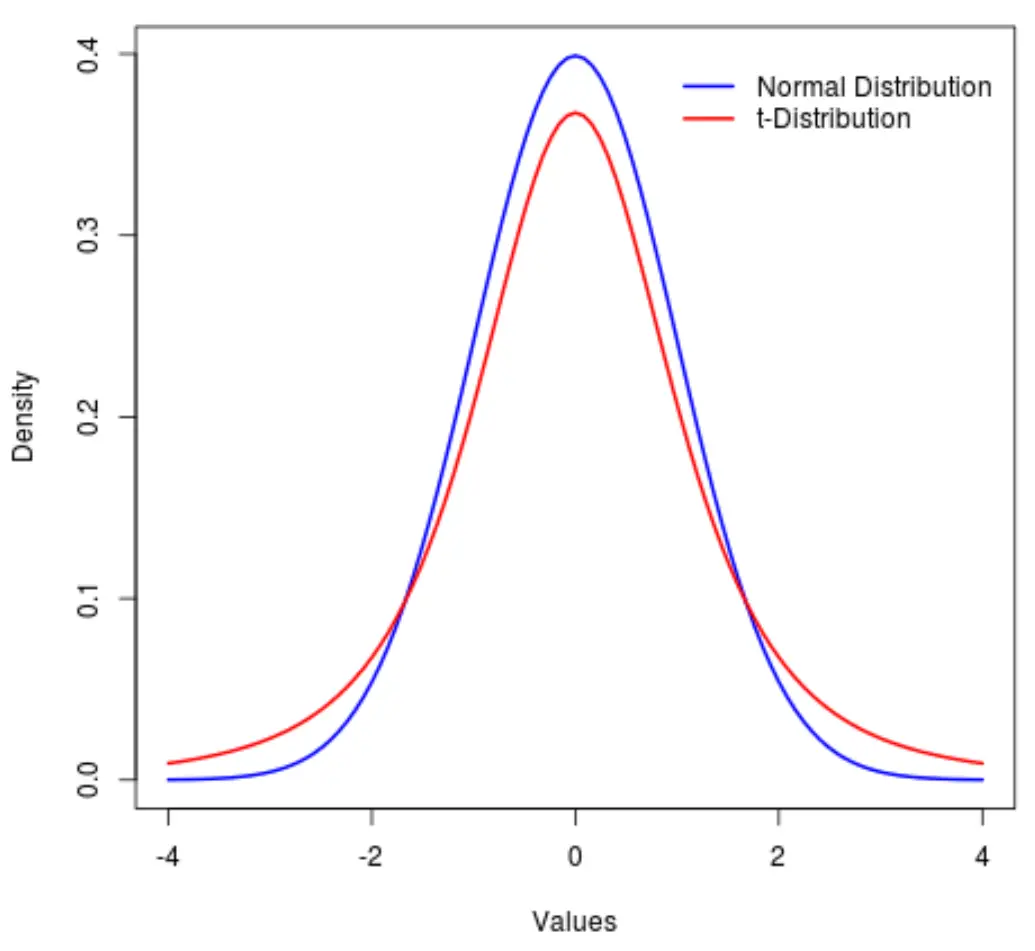
No jargão estatístico, usamos uma métrica chamada curtose para medir o quão “pesada” é uma distribuição. Então, diríamos que a curtose de uma distribuição t é maior do que a de uma distribuição normal.
Na prática, usamos com mais frequência a distribuição t ao realizar testes de hipóteses ou construir intervalos de confiança .
Por exemplo, a fórmula para calcular um intervalo de confiança para uma média populacional é:
Intervalo de confiança = x +/- t 1-α/2, n-1 *(s/√ n )
Ouro:
- x : média amostral
- t: o valor t crítico, com base no nível de significância α e no tamanho da amostra n
- s: desvio padrão da amostra
- n: tamanho da amostra
Nesta fórmula, usamos o valor crítico da tabela t em vez do valor crítico da tabela z quando uma das seguintes condições for verdadeira:
- Não sabemos o desvio padrão da população.
- O tamanho da amostra é menor ou igual a 30.
O fluxograma a seguir fornece uma maneira útil de saber se você deve usar o valor crítico da tabela t ou da tabela z:

A principal diferença entre usar a distribuição t e usar a distribuição normal na construção de intervalos de confiança é que os valores críticos da distribuição t serão maiores, levando a intervalos de confiança mais amplos .
Por exemplo, suponhamos que queremos construir um intervalo de confiança de 95% para o peso médio de uma população de tartarugas, a fim de coletar uma amostra aleatória de tartarugas com as seguintes informações:
- Tamanho da amostra n = 25
- Peso médio da amostra x = 300
- Desvio padrão amostral s = 18,5
O valor crítico de z para um nível de confiança de 95% é 1,96 , enquanto um valor crítico de t para um intervalo de confiança de 95% com df = 25-1 = 24 graus de liberdade é 2,0639 .
Assim, um intervalo de confiança de 95% para a média da população usando um valor crítico z é:
IC 95% = 300 +/- 1,96*(18,5/√ 25 ) = [292,75, 307,25]
Embora um intervalo de confiança de 95% para a média da população usando um valor t-crítico seja:
IC 95% = 300 +/- 2,0639*(18,5/√25) = [292,36, 307,64]
Observe que o intervalo de confiança com o valor t-crítico é mais amplo.
A ideia aqui é que quando temos amostras pequenas temos menos certeza da verdadeira média populacional, por isso é útil usar a distribuição t para produzir intervalos de confiança mais amplos que tenham mais chances de conter a verdadeira média populacional.
Visualização dos graus de liberdade para a distribuição t
Deve-se notar que à medida que os graus de liberdade aumentam, a distribuição t se aproxima da distribuição normal.
Para ilustrar isso, considere o gráfico a seguir que mostra a forma da distribuição t com os seguintes graus de liberdade:
- df = 3
- df = 10
- df = 30
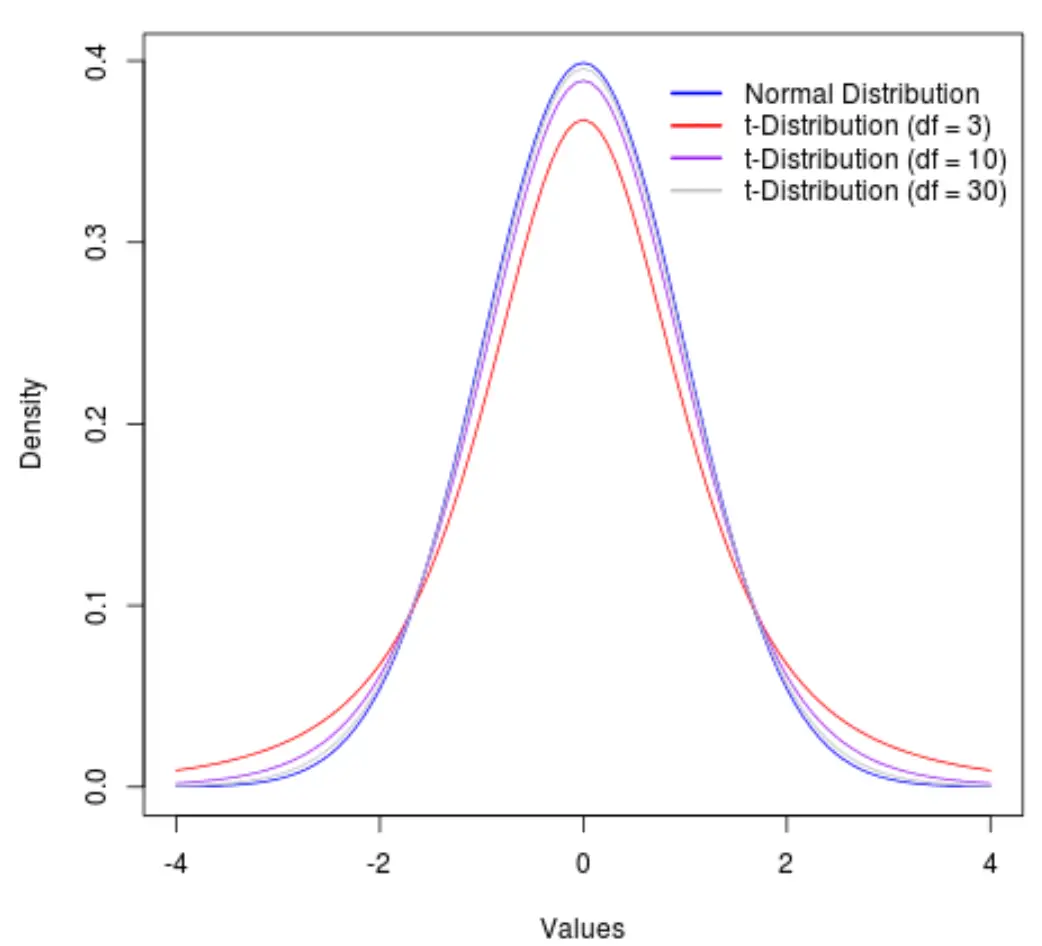
Além dos 30 graus de liberdade, a distribuição t e a distribuição normal tornam-se tão semelhantes que as diferenças entre o uso de um valor t-crítico e um valor z-crítico nas fórmulas tornam-se insignificantes.