Distribuição qui-quadrado
Este artigo explica o que é a distribuição qui-quadrado e para que ela é usada. Além disso, você encontrará o gráfico de distribuição qui-quadrado e suas propriedades.
Qual é a distribuição qui-quadrado?
A distribuição Qui-quadrado é uma distribuição de probabilidade cujo símbolo é χ². Mais precisamente, a distribuição qui-quadrado é a soma do quadrado de k variáveis aleatórias independentes com distribuição normal.
Assim, a distribuição Qui-quadrado possui k graus de liberdade. Portanto, uma distribuição Qui-quadrado tem tantos graus de liberdade quanto a soma dos quadrados das variáveis normalmente distribuídas que ela representa.
![Rendered by QuickLaTeX.com \displaystyle X\sim\chi^2_k \ \color{orange}\bm{\longrightarrow}\color{black}\ \begin{array}{l}\text{Distribuci\'on chi-cuadrado}\\[2ex]\text{con k grados de libertad}\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-9ea0bf7a87071883ceae5e419bae9e71_l3.png)
A distribuição qui-quadrado também é conhecida como distribuição de Pearson .
Deve-se notar que a distribuição Qui-quadrado é um caso especial da distribuição gama.
A distribuição qui-quadrado é amplamente utilizada em inferência estatística, por exemplo, em testes de hipóteses e intervalos de confiança. Veremos a seguir quais são as aplicações desse tipo de distribuição de probabilidade.
Gráfico de distribuição qui-quadrado
Assim que vermos a definição da distribuição Qui-quadrado, veremos vários exemplos deste tipo de distribuição representados graficamente. Abaixo você pode ver como o gráfico de probabilidade da distribuição qui-quadrado varia dependendo dos graus de liberdade.
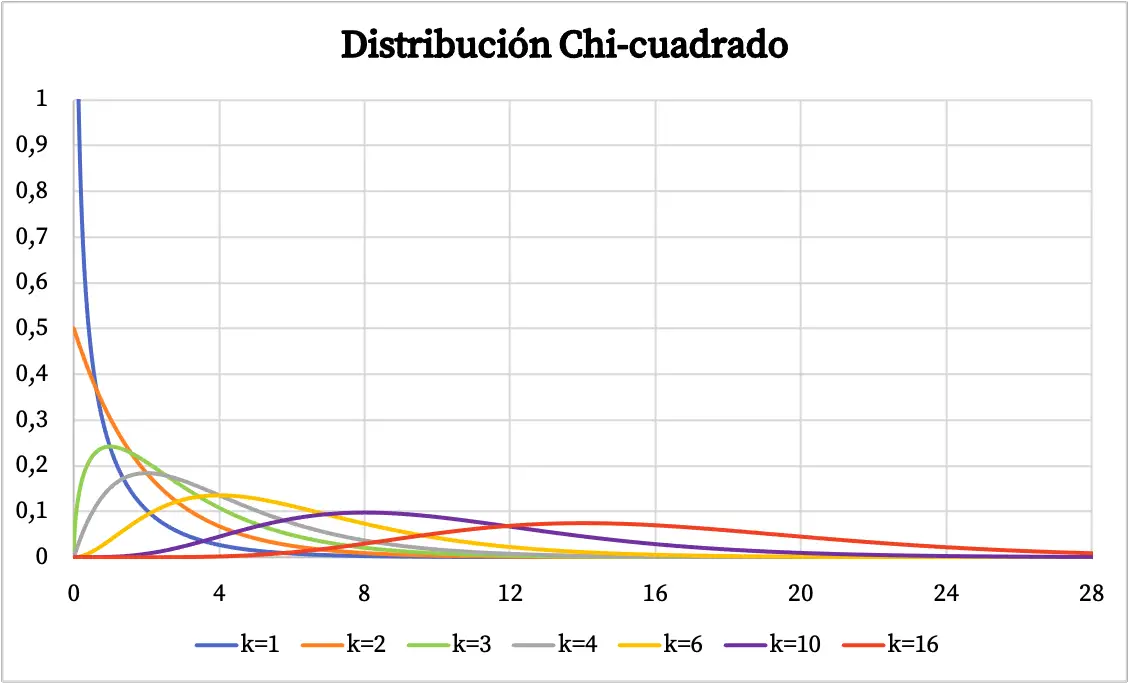
A função de densidade da distribuição Qui-quadrado foi representada no gráfico acima. Por outro lado, o gráfico da função de distribuição de probabilidade cumulativa qui-quadrado é o seguinte:
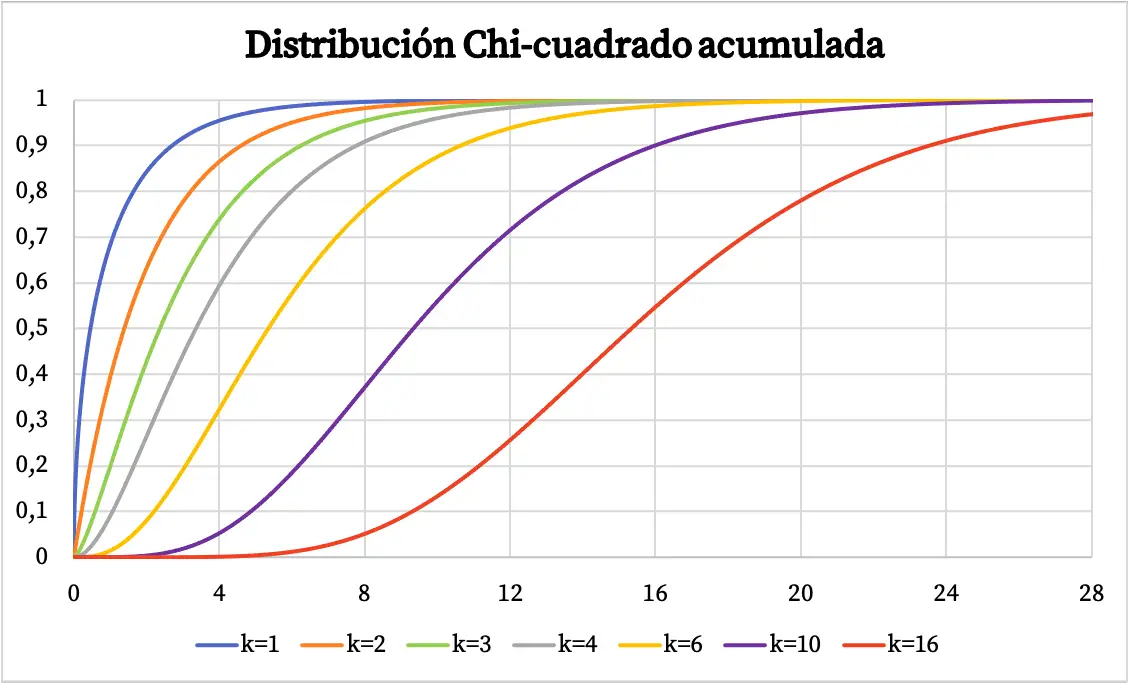
Características da distribuição qui-quadrado
Nesta seção veremos as propriedades mais importantes da distribuição Qui-quadrado relacionadas à teoria das probabilidades e à estatística.
- A média de uma distribuição qui-quadrado é igual aos seus graus de liberdade.
![Rendered by QuickLaTeX.com \begin{array}{c}X\sim\chi^2_k\\[2ex] E[X]=k\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-8a7926aa60ec788064c47a5a34e641ab_l3.png)
- A variância de uma distribuição Qui-quadrado é igual a duas vezes os graus de liberdade da distribuição.
![Rendered by QuickLaTeX.com \begin{array}{c}X\sim\chi^2_k\\[2ex] Var(X)=2\cdot k\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-cffd659f19d8ed8260fcaf53dc6dd83f_l3.png)
- A moda de uma distribuição qui-quadrado é duas unidades a menos que seus graus de liberdade, desde que a distribuição tenha mais de um grau de liberdade.
![]()
- A função densidade da distribuição Qui-quadrado é zero se x=0. Porém, para valores de x maiores que 0, a função densidade de uma distribuição Qui-quadrado é definida pela seguinte fórmula:
![]()
- A função de distribuição cumulativa da distribuição Qui-quadrado é governada pela seguinte fórmula:
![]()
- O coeficiente de assimetria da distribuição Qui-quadrado é a raiz quadrada do quociente de oito dividido pelo número de graus de liberdade da distribuição.
![]()
- A curtose da distribuição Qui-quadrado é calculada usando a seguinte expressão:
![]()
- Devido ao teorema do limite central, a distribuição qui-quadrado pode ser aproximada por uma distribuição normal se k for grande o suficiente.
![]()
Aplicações da distribuição qui-quadrado
A distribuição qui-quadrado tem muitas aplicações diferentes em estatística. Na verdade, existe até o teste do qui-quadrado que é utilizado para verificar a independência entre as variáveis e a qualidade do ajuste a uma distribuição teórica. Por exemplo, o teste Qui-quadrado pode ser usado para determinar se os dados de uma amostra estão em conformidade com uma distribuição de Poisson.
Na análise de regressão linear, a distribuição qui-quadrado também é usada para estimar a média de uma população normalmente distribuída e para estimar a inclinação da linha de estudo de regressão linear.
Por fim, a distribuição Qui-quadrado também participa da análise de variância, através da sua relação com a distribuição F de Snedecor.