Distribuição simétrica: definição + exemplos
Nas estatísticas, uma distribuição simétrica é aquela em que os lados esquerdo e direito se espelham.
A distribuição simétrica mais conhecida é a distribuição normal , que possui um formato de sino distinto.
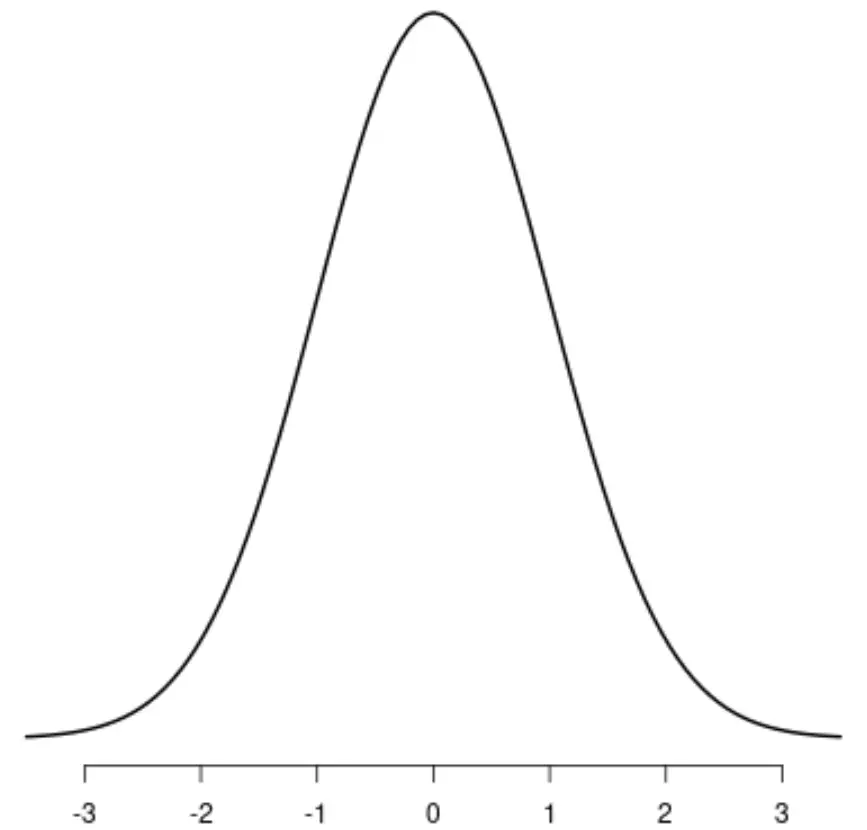
Se você traçasse uma linha no centro da distribuição, os lados esquerdo e direito da distribuição se espelhariam perfeitamente:
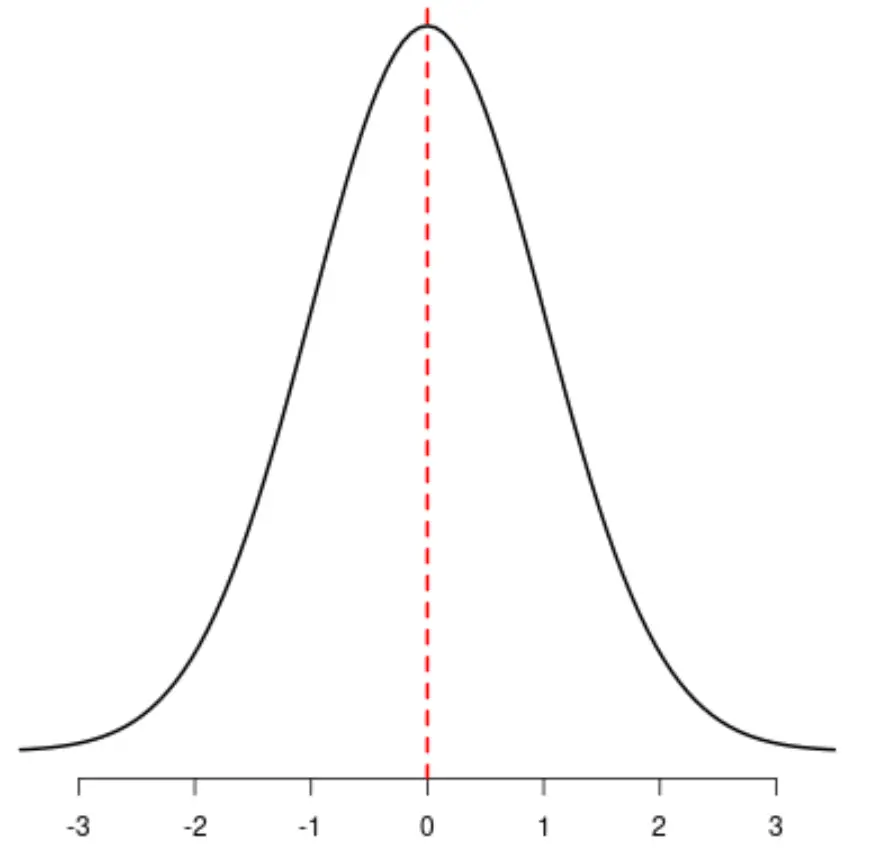
Nas estatísticas, a assimetria é uma forma de descrever a simetria de uma distribuição. Este valor pode ser negativo, zero ou positivo.
Para distribuições simétricas, a assimetria é zero.
Isso contrasta com distribuições distorcidas à esquerda, que apresentam assimetria negativa:
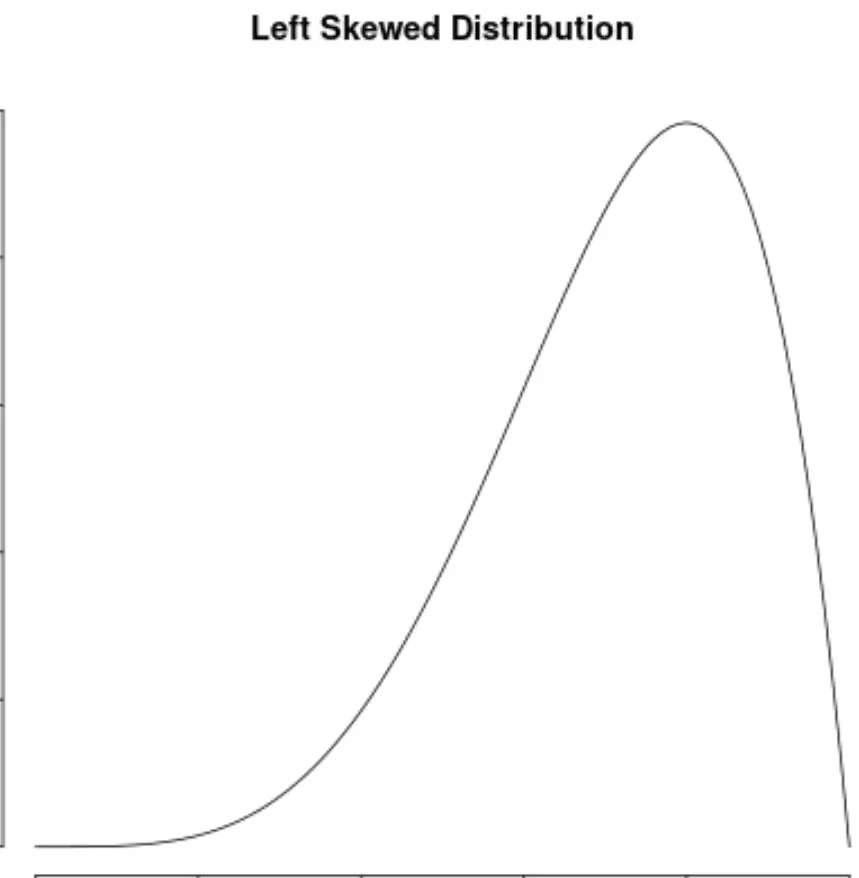
Isso também contrasta com distribuições distorcidas à direita, que apresentam assimetria positiva:
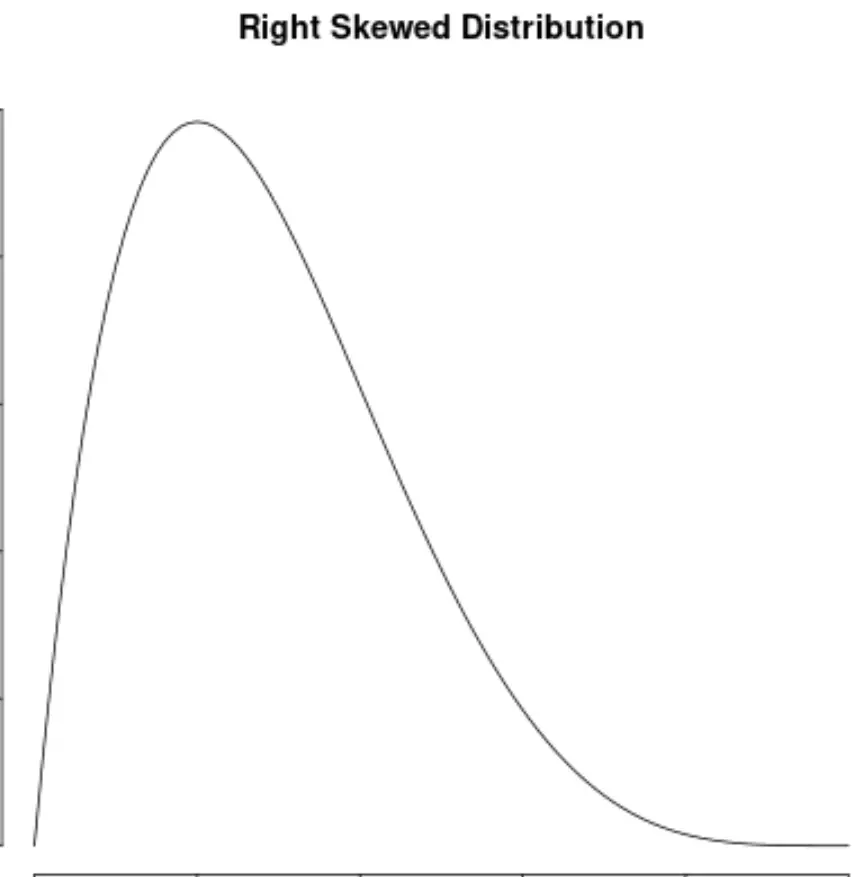
Propriedades de distribuições simétricas
Em uma distribuição simétrica, a média, a mediana e a moda são todas iguais.

Lembre-se das seguintes definições para cada um:
- Média: o valor médio.
- Mediana: o valor médio.
- Moda: o valor que aparece com mais frequência.
Numa distribuição simétrica, cada um desses valores é igual ao outro.
Em cada um dos exemplos até agora, usamos distribuições unimodais como exemplos – distribuições com apenas um “pico”. No entanto, uma distribuição também pode ser bimodal e simétrica.
Uma distribuição bimodal é uma distribuição que possui dois picos.
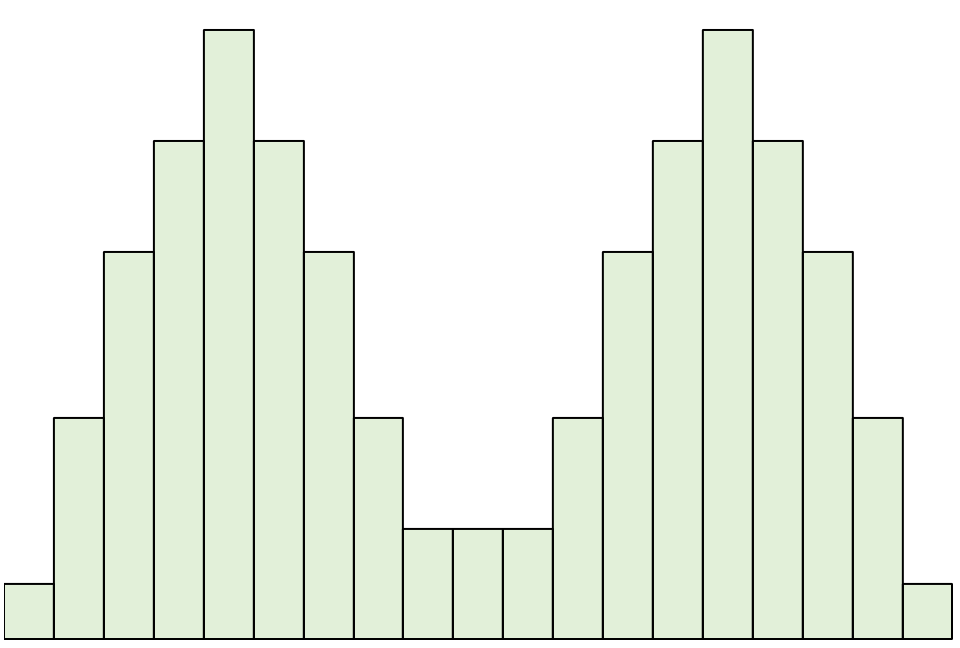
Observe que se traçarmos uma linha no centro desta distribuição, os lados esquerdo e direito ainda se espelhariam.
Para essas distribuições, a média e a mediana são iguais. No entanto, a moda está em ambos os vértices.
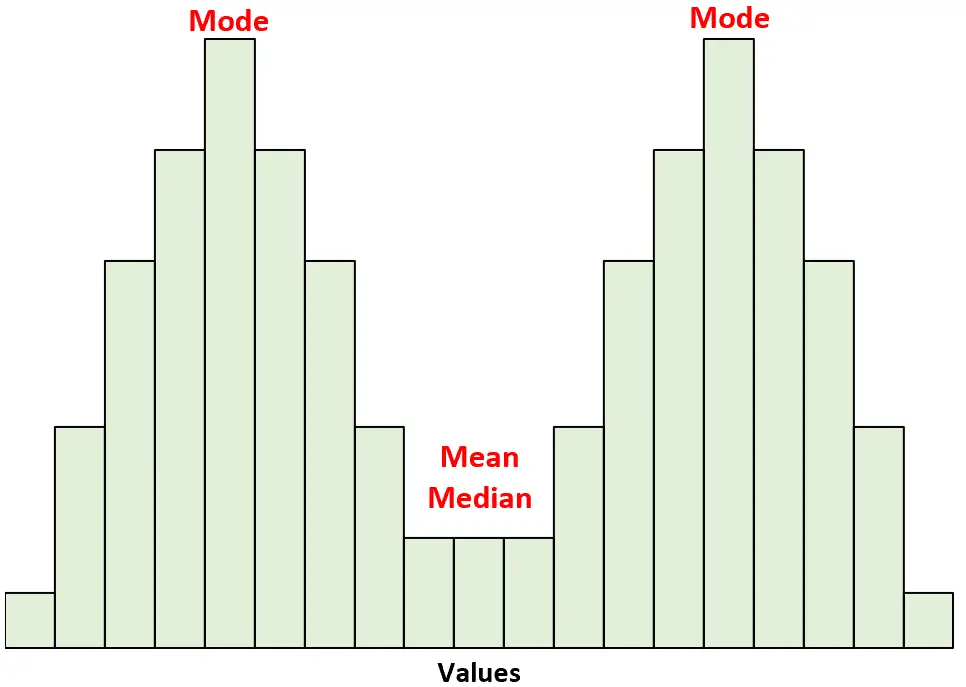
Outros exemplos de distribuições simétricas
Além da distribuição normal, as seguintes distribuições também são simétricas:
A distribuição t
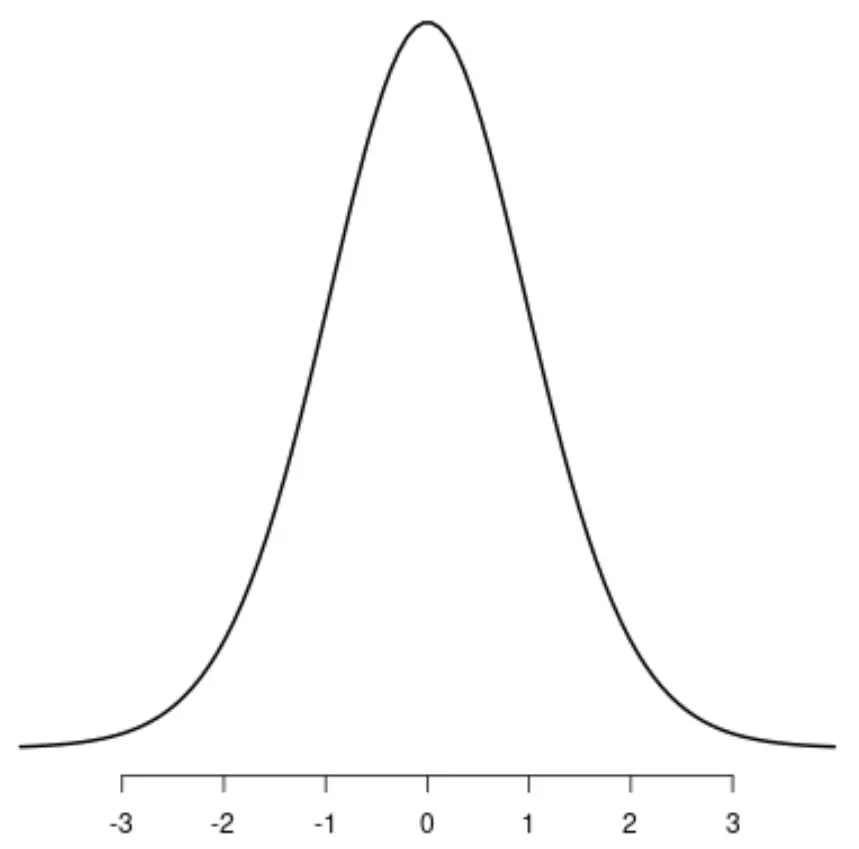
Distribuição uniforme

A distribuição de Cauchy
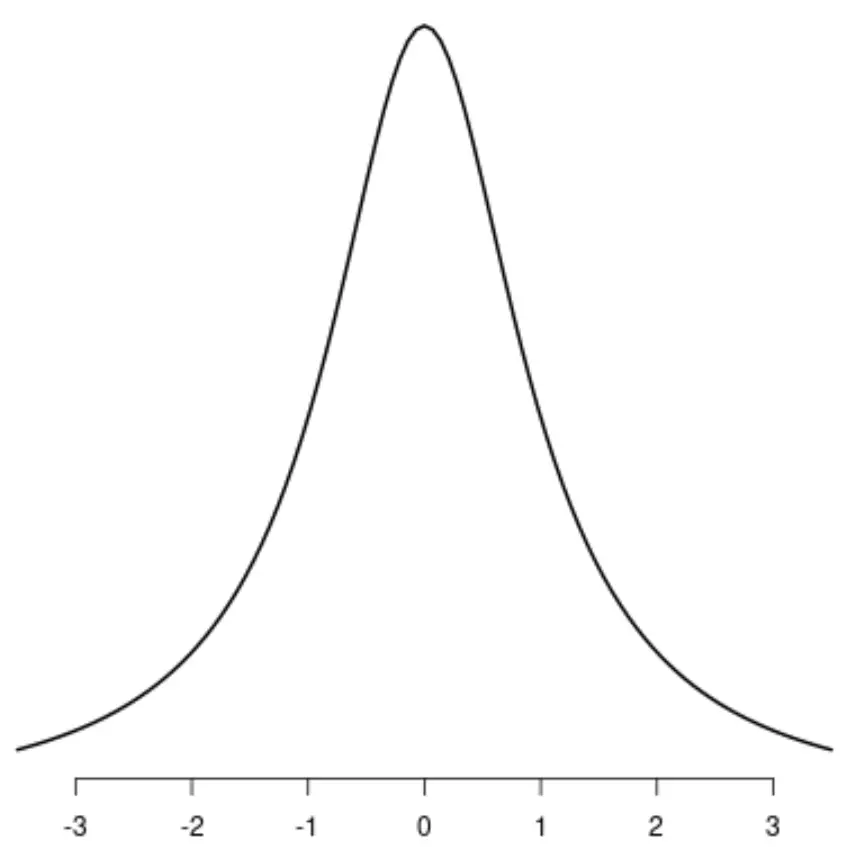
Se você traçasse uma linha no centro de uma dessas distribuições, os lados esquerdo e direito de cada distribuição se espelhariam perfeitamente.
Distribuições simétricas e o teorema do limite central
Um dos teoremas mais importantes em todas as estatísticas é o teorema do limite central, que afirma que a distribuição amostral de uma média amostral é aproximadamente normal se o tamanho da amostra for grande o suficiente, mesmo que a distribuição populacional não seja normal .
Para aplicar o teorema do limite central, o tamanho da amostra deve ser grande o suficiente. Acontece que o número exacto de pessoas “suficientemente grandes” depende da forma subjacente da distribuição da população.
Especialmente:
- Se a distribuição da população for simétrica, um tamanho de amostra tão pequeno quanto 15 é por vezes suficiente.
- Se a distribuição da população for distorcida, normalmente é necessária uma amostra de pelo menos 30 pessoas.
- Se a distribuição da população for extremamente distorcida, poderá ser necessária uma amostra de 40 ou mais pessoas.
Portanto, a vantagem das distribuições simétricas é que precisamos de amostras menores para aplicar o teorema do limite central ao calcular intervalos de confiança ou realizar testes de hipóteses .
Recursos adicionais
Uma introdução ao teorema do limite central
O que é uma distribuição bimodal?
Um guia para distribuições distorcidas à esquerda e à direita