Uma introdução à distribuição triangular

A distribuição triangular é uma distribuição de probabilidade contínua com uma função de densidade de probabilidade em forma de triângulo.

É definido por três valores:

• O valor mínimo tem
• O valor máximo b
• O valor máximo c

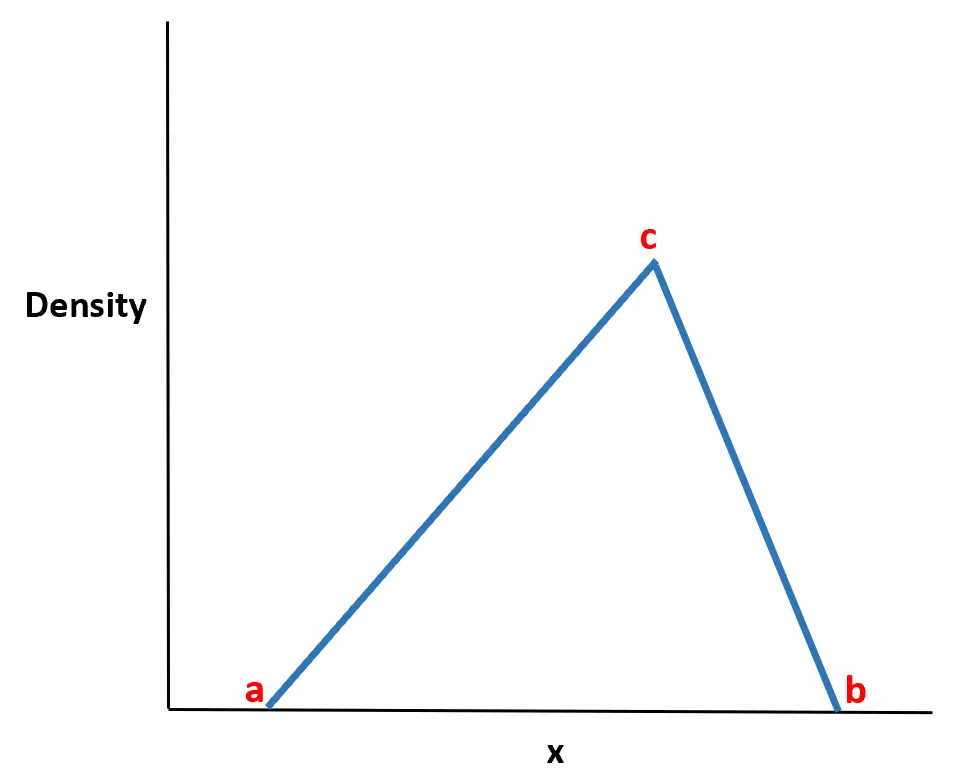
O nome da distribuição vem do fato de que a função densidade de probabilidade tem a forma de um triângulo.

Acontece que esta distribuição é extremamente útil no mundo real porque muitas vezes podemos estimar o valor mínimo (a), o valor máximo (b) e o valor mais provável (c) que uma variável aleatória assumirá. muitas vezes pode modelar o comportamento de variáveis aleatórias usando uma distribuição triangular conhecendo apenas esses três valores.

Por exemplo, um restaurante pode estimar que suas vendas totais para a próxima semana serão de no mínimo US$ 10.000, no máximo de US$ 30.000 e, muito provavelmente, de US$ 25.000.

Usando apenas esses três números, eles poderiam usar uma distribuição triangular para determinar a probabilidade de realizar um determinado número de vendas.

Propriedades da distribuição triangular

A distribuição triangular tem as seguintes propriedades:

PDF:

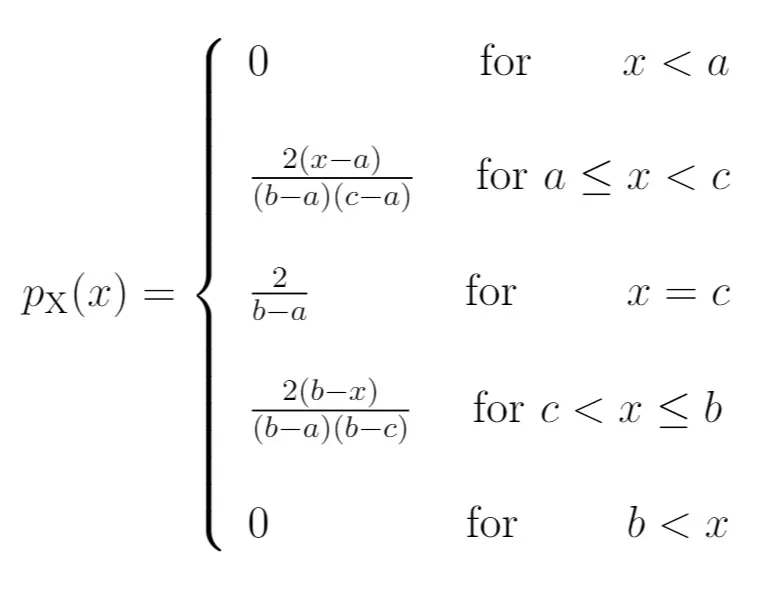
CDF:

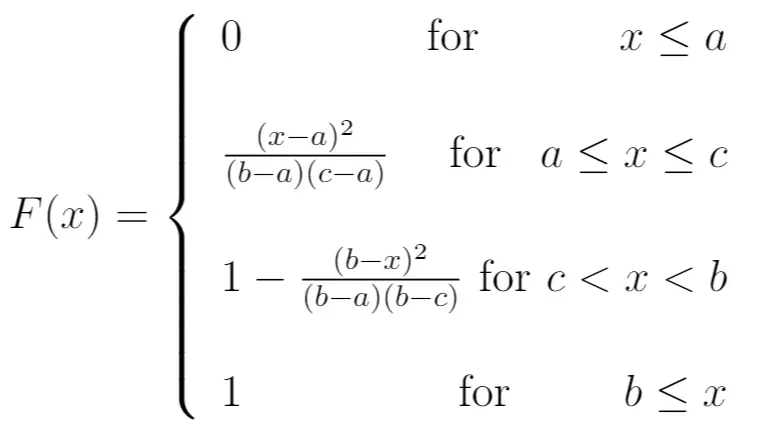
Média: (a + b + c) / 3

Modo: c

Variância: (a ² + b ² + c ² – ab – ac – bc) / 18

Exemplo de uso da distribuição triangular

Voltemos ao exemplo anterior. Digamos que um restaurante estime que suas vendas totais na próxima semana serão de no mínimo US$ 10.000, no máximo de US$ 30.000 e, muito provavelmente, de US$ 25.000.

Qual é a probabilidade de o restaurante ter vendas totais inferiores a US$ 20.000?

Para responder a esta pergunta, podemos perguntar x = vendas totais. Sabemos que x está entre o valor mínimo a de US$ 10.000 e o valor máximo c de US$ 25.000.

Portanto, de acordo com o PDF, podemos usar a seguinte equação para encontrar a probabilidade de o restaurante ter menos de US$ 20.000 em vendas totais:

• P(X <$20.000) = (xa) ² / ((ba)(ca))
• P(X <US$ 20.000) = (20.000-10.000) ² / ((30.000-10.000)(25.000-10.000))
• P(X <US$ 20.000) = 0,333

A probabilidade de o restaurante ter vendas totais inferiores a US$ 20.000 é de 0,333 .

Qual é a média de vendas esperada para o restaurante?

Podemos calcular as vendas médias esperadas usando a fórmula da média fornecida anteriormente:

• Média = (a + b + c) / 3
• Média = (US$ 10.000 + US$ 30.000 + US$ 25.000) / 3
• Média = $ 21.667

As vendas médias esperadas são de 21.667 .

Recursos adicionais

Os tutoriais a seguir fornecem introduções a outras distribuições comumente usadas:

A distribuição normal
A distribuição binomial
A distribuição dos peixes
A distribuição geométrica