O que é uma distribuição unimodal? (definição e #038; exemplo)

Uma distribuição unimodal é uma distribuição de probabilidade com um pico claro.

Isto contrasta com uma distribuição bimodal , que tem dois picos claros:

Isto também contrasta com uma distribuição multimodal , que tem dois ou mais picos:

Nota: Uma distribuição bimodal é apenas um tipo específico de distribuição multimodal.

Exemplos de distribuições unimodais

Aqui estão alguns exemplos de distribuições unimodais na prática.

Exemplo 1: Peso ao nascer dos bebês

É sabido que a distribuição de peso dos recém-nascidos segue uma distribuição unimodal com média em torno de 7,5 quilos. Se criarmos um histograma do peso dos bebês, veremos um “pico” de 7,5 quilos, com alguns bebês pesando mais e outros pesando menos.

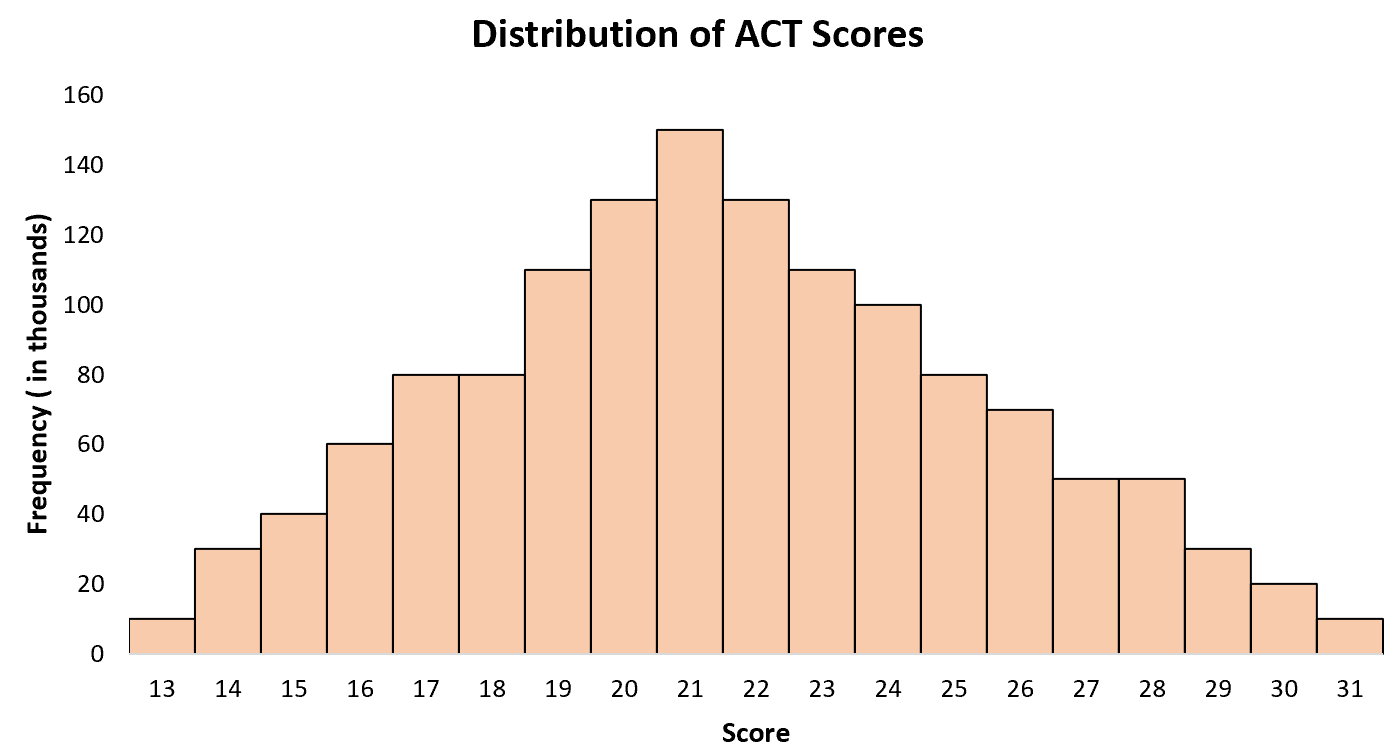
Exemplo 2: pontuações do ACT

A pontuação média do ACT para estudantes do ensino médio nos Estados Unidos é de cerca de 21, com alguns alunos com pontuação mais baixa e outros com pontuação mais alta. Se criarmos um histograma de pontuações do ACT para todos os alunos nos Estados Unidos, veremos um único “pico” aos 21 anos, com pontuações mais altas para alguns alunos e pontuações mais baixas para outros.

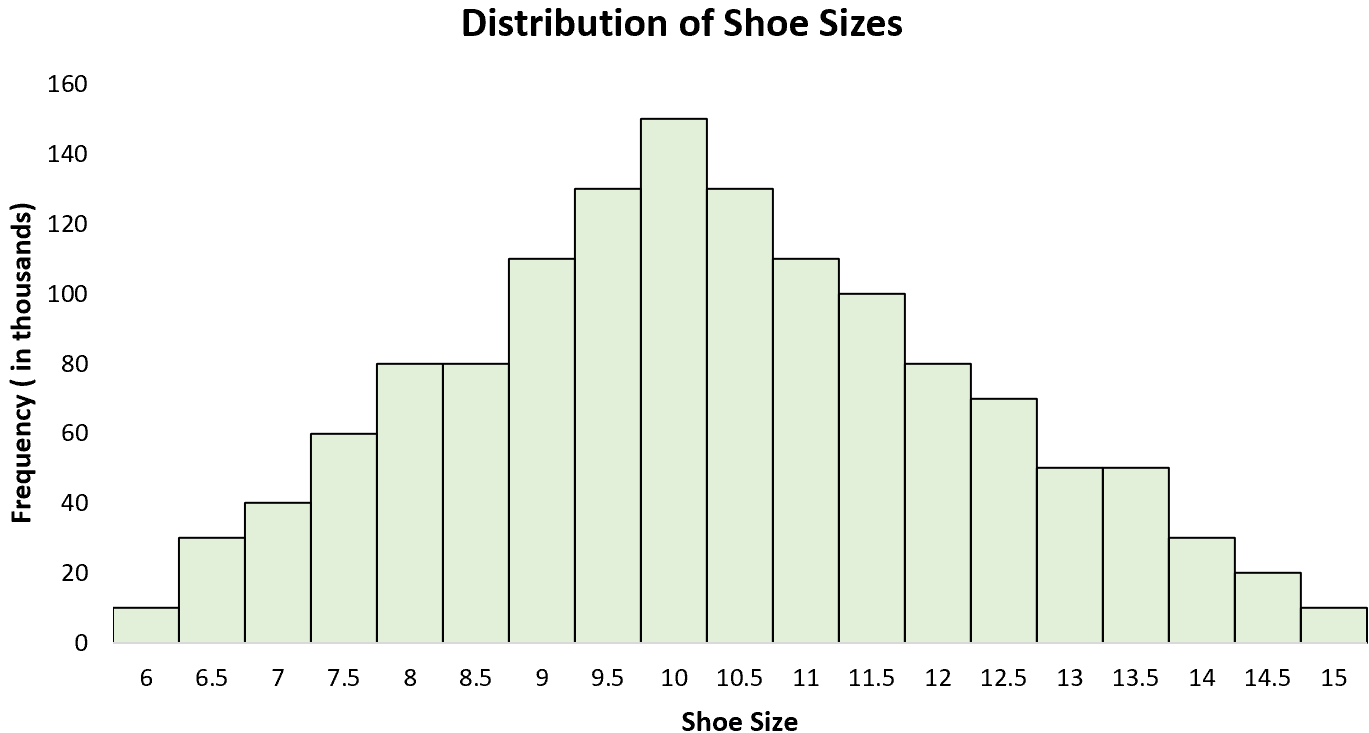
Exemplo 3: tamanhos de calçado

A distribuição dos tamanhos de calçados masculinos é uma distribuição unimodal com um “pico” em torno de 10. Se criarmos um histograma de todos os tamanhos de calçados masculinos, veremos um único pico em 10, com alguns homens usando um tamanho de calçado maior e outros usando um tamanho maior. tamanho. tamanho menor.

Distribuições unimodais em estatísticas

As seguintes distribuições de probabilidade em estatísticas são todas distribuições unimodais:

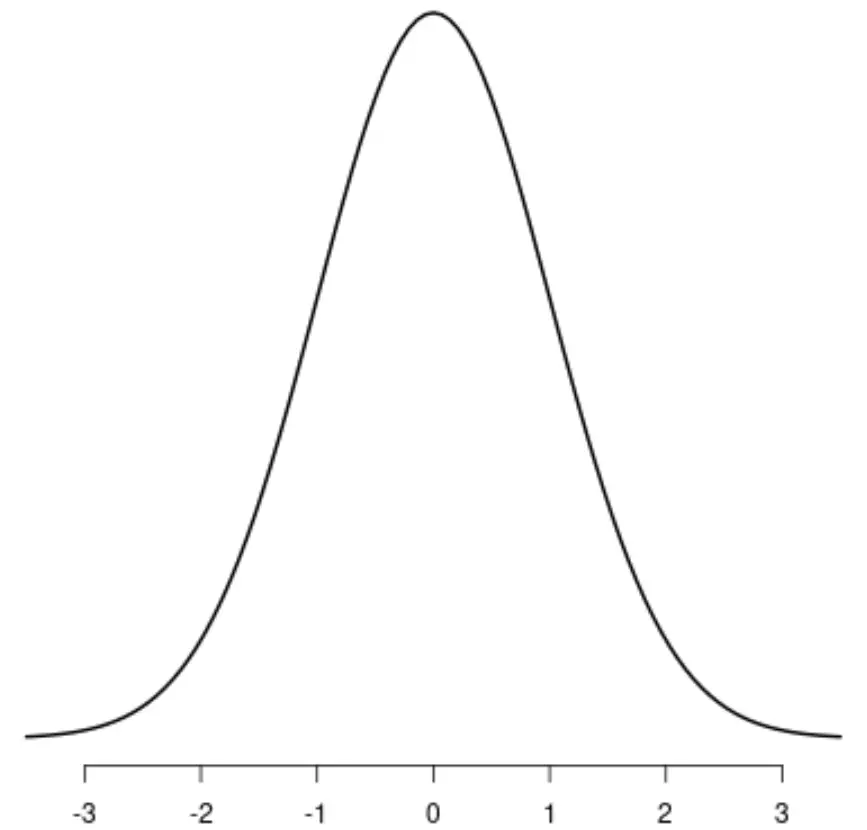
A distribuição normal

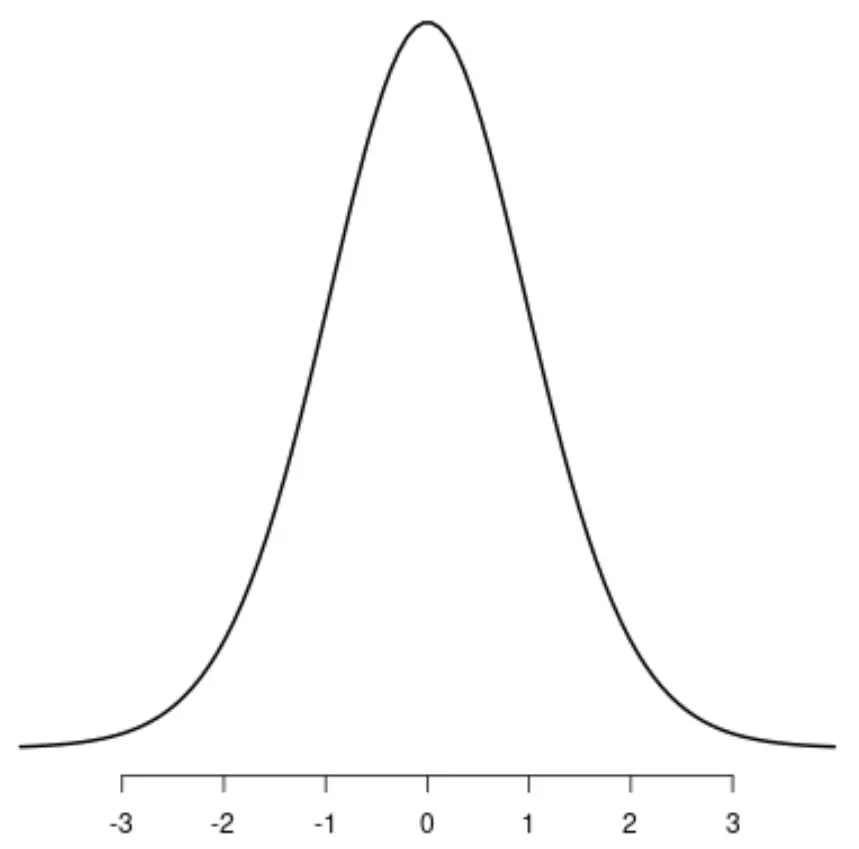
A distribuição t

Distribuição uniforme

A distribuição de Cauchy

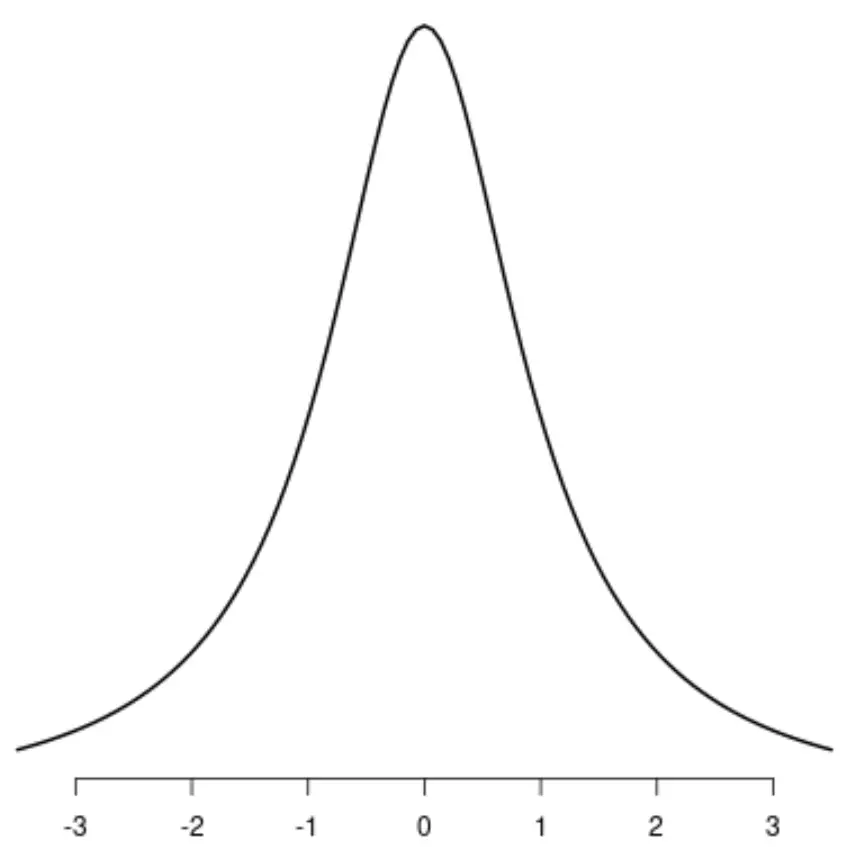
Observe que cada uma dessas distribuições possui um único pico distinto.

Como analisar distribuições unimodais

Freqüentemente descrevemos distribuições unimodais usando três medidas diferentes de tendência central :

• Média : O valor médio
• Mediana : o valor mediano
• Moda : O valor que aparece com mais frequência

Dependendo da assimetria da distribuição, estas três medidas podem ser encontradas em locais diferentes.

Distribuição enviesada à esquerda: Média < Mediana < Moda

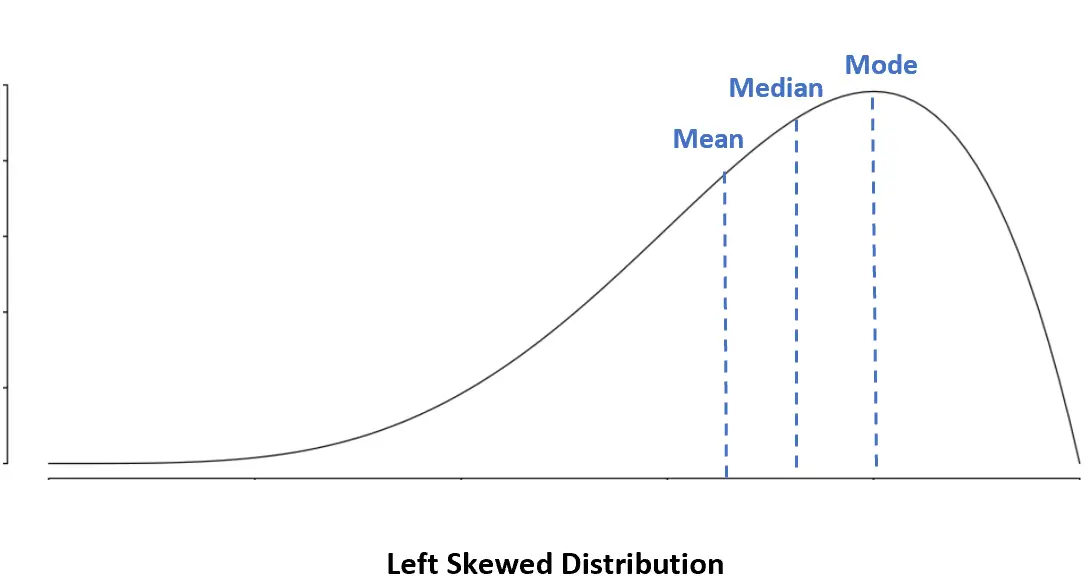
Numa distribuição enviesada à esquerda, a média é menor que a mediana.

Distribuição enviesada à direita: Moda < Mediana < Média

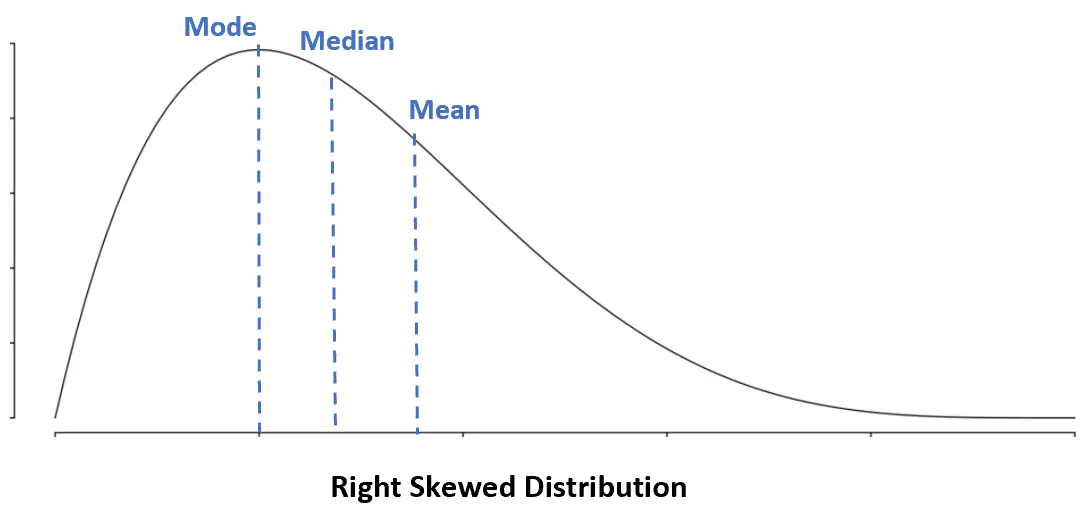
Numa distribuição distorcida à direita, a média é maior que a mediana.

Sem viés: Média = Mediana = Moda

Em uma distribuição simétrica, a média, a mediana e a moda são todas iguais.

Recursos adicionais

Distribuições distorcidas para a esquerda ou para a direita
Distribuições simétricas: definição + exemplos