Distribuição weibull

By Dr. benjamim anderson Agosto 3, 2023 Probabilidade 0 Comments

Este artigo explica o que é a distribuição Weibull e para que é usada. Além disso, você poderá ver a representação gráfica da distribuição Weibull e quais são as propriedades deste tipo de distribuição de probabilidade.

Qual é a distribuição Weibull?

A distribuição Weibull é uma distribuição de probabilidade contínua definida por dois parâmetros característicos: o parâmetro de forma α e o parâmetro de escala λ.

Nas estatísticas, a distribuição Weibull é usada principalmente para análise de sobrevivência. Da mesma forma, a distribuição Weibull tem muitas aplicações em diferentes campos. Entraremos em detalhes sobre o uso da distribuição Weibull abaixo.

$X\sim\text{Weibull}(\alpha,\lambda)$

Segundo os autores, a distribuição Weibull também pode ser parametrizada com três parâmetros. Em seguida, é adicionado um terceiro parâmetro denominado valor limite, que indica a abcissa na qual o gráfico de distribuição começa.

A distribuição Weibull recebeu o nome do sueco Waloddi Weibull, que a descreveu detalhadamente em 1951. No entanto, a distribuição Weibull foi descoberta por Maurice Fréchet em 1927 e aplicada pela primeira vez por Rosin e Rammler em 1933.

Traçando a distribuição Weibull

Depois de vermos a definição da distribuição Weibull, veremos como sua representação gráfica varia em função dos valores de seus parâmetros.

Abaixo você pode ver vários exemplos de como o gráfico da função densidade da distribuição Weibull varia dependendo do valor do parâmetro de forma e do parâmetro de escala.

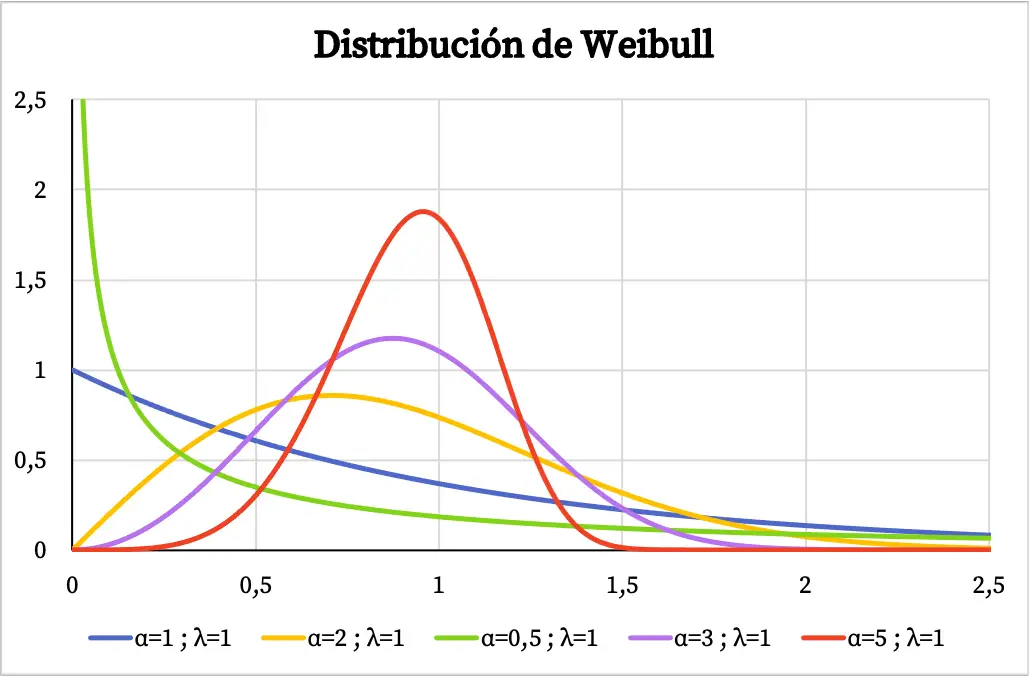
Quando a distribuição Weibull é usada para modelar a taxa de falha de um sistema em função do tempo, o valor do parâmetro de forma α significa o seguinte:

α<1: a taxa de falha diminui com o tempo.
α=1: a taxa de falhas é constante ao longo do tempo.
α>1: a taxa de falha aumenta com o tempo.

Por outro lado, no gráfico a seguir você pode ver a função de probabilidade cumulativa da distribuição Weibull traçada com base em seus valores característicos.

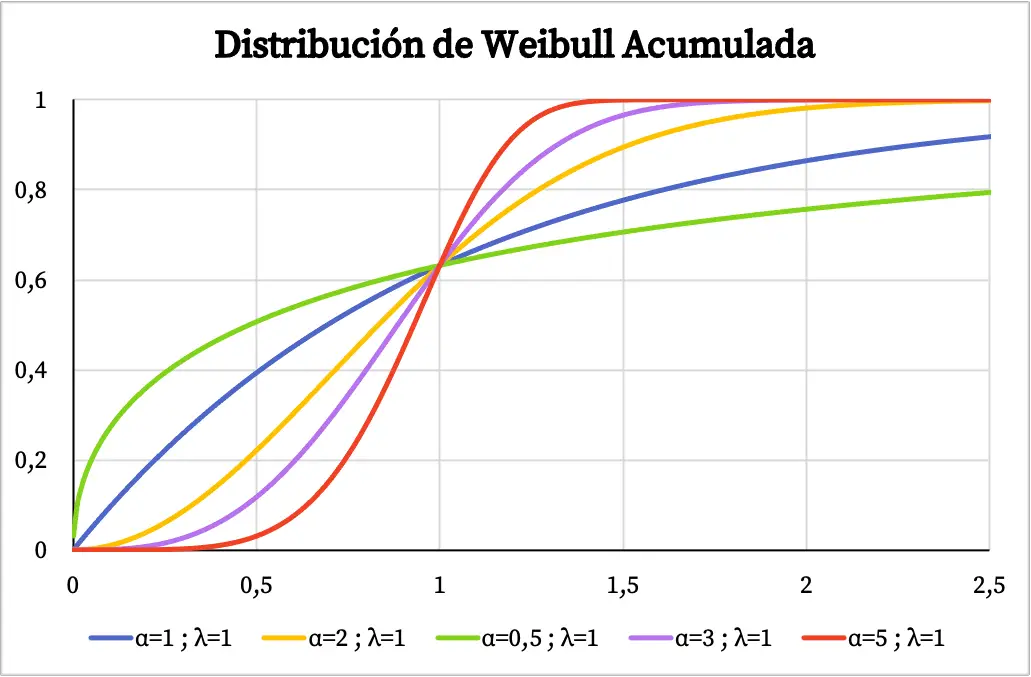
Características da distribuição Weibull

A distribuição Weibull possui as seguintes características:

A distribuição Weibull possui dois parâmetros característicos que definem seu gráfico: o parâmetro de forma α e o parâmetro de escala λ. Ambos os parâmetros são números reais positivos.

$\begin{array}{c}\alpha >0\\[2ex]\lambda >0\\[2ex]\text{Weibull}(\alpha,\lambda)\end{array}” title=”Rendered by QuickLaTeX.com” height=”92″ width=”101″ style=”vertical-align: 0px;”></p> </p> <ul> <li> A distribuição Weibull aceita apenas valores de abcissas positivos.</li> </ul> <p class=$ $x\in (0,+\infty)$

A média da distribuição Weibull é calculada com a seguinte fórmula:

$\displaystyle E[X]=\frac{1}{\lambda}\;\Gamma\left(1+\frac{1}{\alpha}\right)$

Por outro lado, a fórmula para encontrar a variância da distribuição Weibull é:

$\displaystyle Var(X)=\frac{1}{\lambda^2}\left[\Gamma\left(1+\frac{2}{\alpha}\right)-\Gamma^2\left(1+\frac{1}{\alpha}\right)\right]$

A moda de uma variável aleatória que segue uma distribuição Weibull com α>1 pode ser determinada pela seguinte expressão:

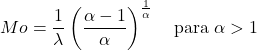
$\displaystyle Mo=\frac{1}{\lambda}\left(\frac{\alpha-1}{\alpha} \right)^{\frac{1}{\alpha}} \quad \text{para } \alpha>1″ title=”Rendered by QuickLaTeX.com” height=”50″ width=”257″ style=”vertical-align: -17px;”></p> </p> <ul> <li> A fórmula para a função densidade da distribuição Weibull é:</li> </ul> <p class=$ $\displaystyle P[X=x]=\lambda\alpha(\lambda x)^{\alpha-1}e^{-(\lambda x)^\alpha}$

Da mesma forma, a fórmula para a função de probabilidade cumulativa da distribuição Weibull é:

$\displaystyle P[X\leq x]=1- e^{-(\lambda x)^\alpha}$

O coeficiente de assimetria da distribuição Weibull é calculado aplicando a seguinte fórmula:

$\displaystyle A=\frac{\displaystyle\Gamma\left(1+\frac{3}{\alpha}\right)\frac{|}{\lambda^3}-3\mu\sigma^2-\mu^3}{\sigma^3}$

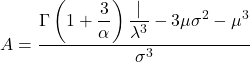
Por último, a fórmula que permite determinar o coeficiente de curtose da distribuição Weibull é a seguinte:

$\displaystyle C=\frac{\displaystyle\frac{1}{\lambda^4}\Gamma \left(1+\frac{4}{\alpha}\right)-4\gamma_{1}\sigma^3\mu-6\mu^2\sigma^2-\mu^4}{\sigma^4}$

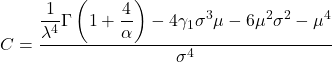
Ouro

$\Gamma_i=\Gamma\left(1+\frac{i}{\alpha}\right).$

Aplicações da distribuição Weibull

A distribuição Weibull tem muitas aplicações, incluindo:

Na estatística aplicada, a distribuição Weibull é utilizada na análise de sobrevivência.
Na engenharia, a distribuição Weibull é usada para modelar funções relacionadas ao tempo de fabricação.
Em sistemas de radar, para simular a dispersão do sinal recebido.
No setor de seguros, para modelar a extensão dos sinistros.
Em meteorologia, por exemplo, para modelar a frequência de diferentes velocidades do vento.

About Author

Dr. benjamim anderson

Olá, sou Benjamin, um professor aposentado de estatística que se tornou professor dedicado na Statorials. Com vasta experiência e conhecimento na área de estatística, estou empenhado em compartilhar meu conhecimento para capacitar os alunos por meio de Statorials. Saber mais