Qual é o erro padrão da estimativa? (definição e #038; exemplo)
O erro padrão da estimativa é uma forma de medir a precisão das previsões feitas por um modelo de regressão.
Frequentemente notado como σ est , é calculado da seguinte forma:
σ é = √ Σ(y – ŷ) 2 /n
Ouro:
- y: O valor observado
- ŷ: O valor previsto
- n: O número total de observações
O erro padrão da estimativa nos dá uma ideia de quão bem um modelo de regressão se ajusta a um conjunto de dados. Especialmente:
- Quanto menor o valor, melhor o ajuste.
- Quanto maior o valor, pior o ajuste.
Para um modelo de regressão com um pequeno erro padrão da estimativa, os pontos de dados serão fortemente agrupados em torno da linha de regressão estimada:
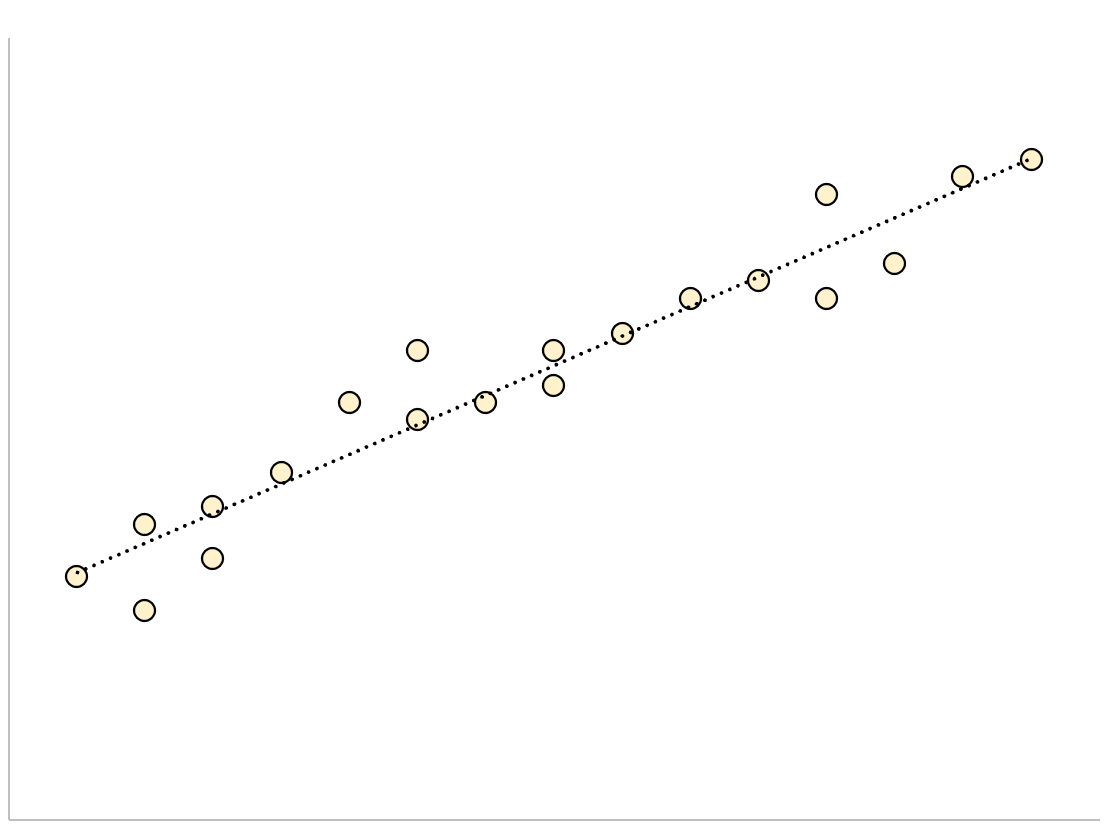
Por outro lado, para um modelo de regressão com um grande erro padrão de estimativa, os pontos de dados estarão mais vagamente espalhados ao redor da linha de regressão:
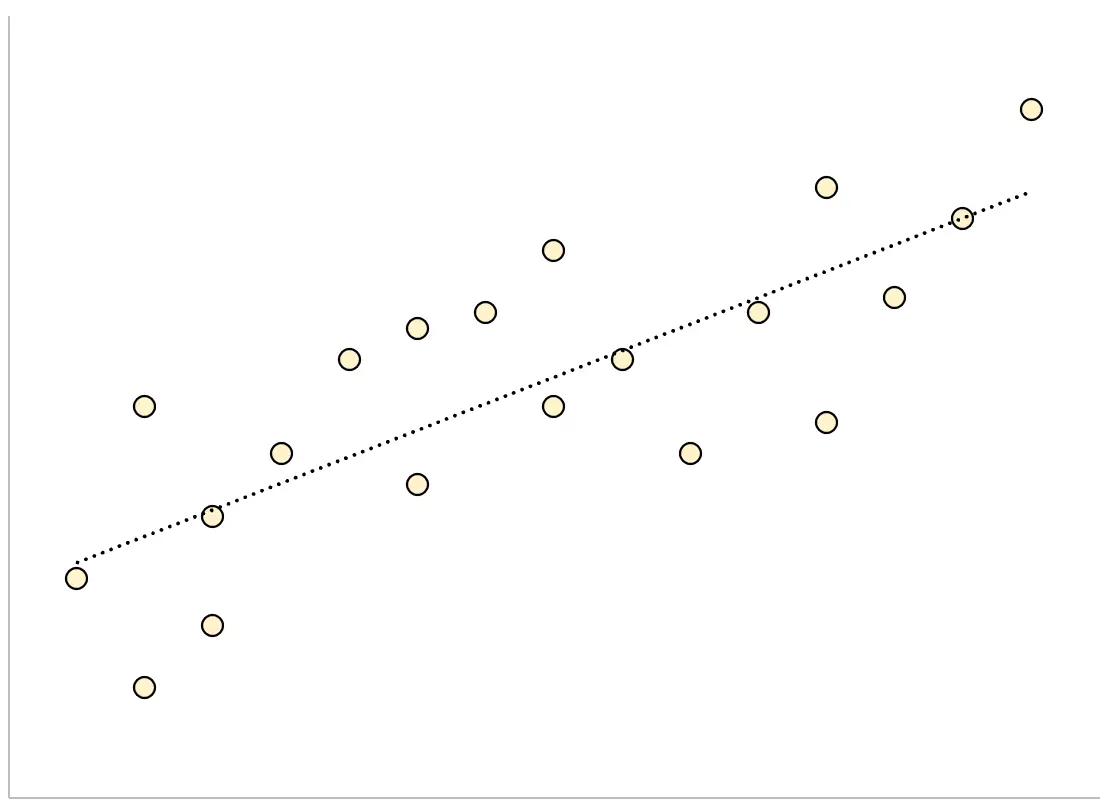
O exemplo a seguir mostra como calcular e interpretar o erro padrão da estimativa para um modelo de regressão no Excel.
Exemplo: erro padrão de estimativa no Excel
Use as etapas a seguir para calcular o erro padrão da estimativa para um modelo de regressão no Excel.
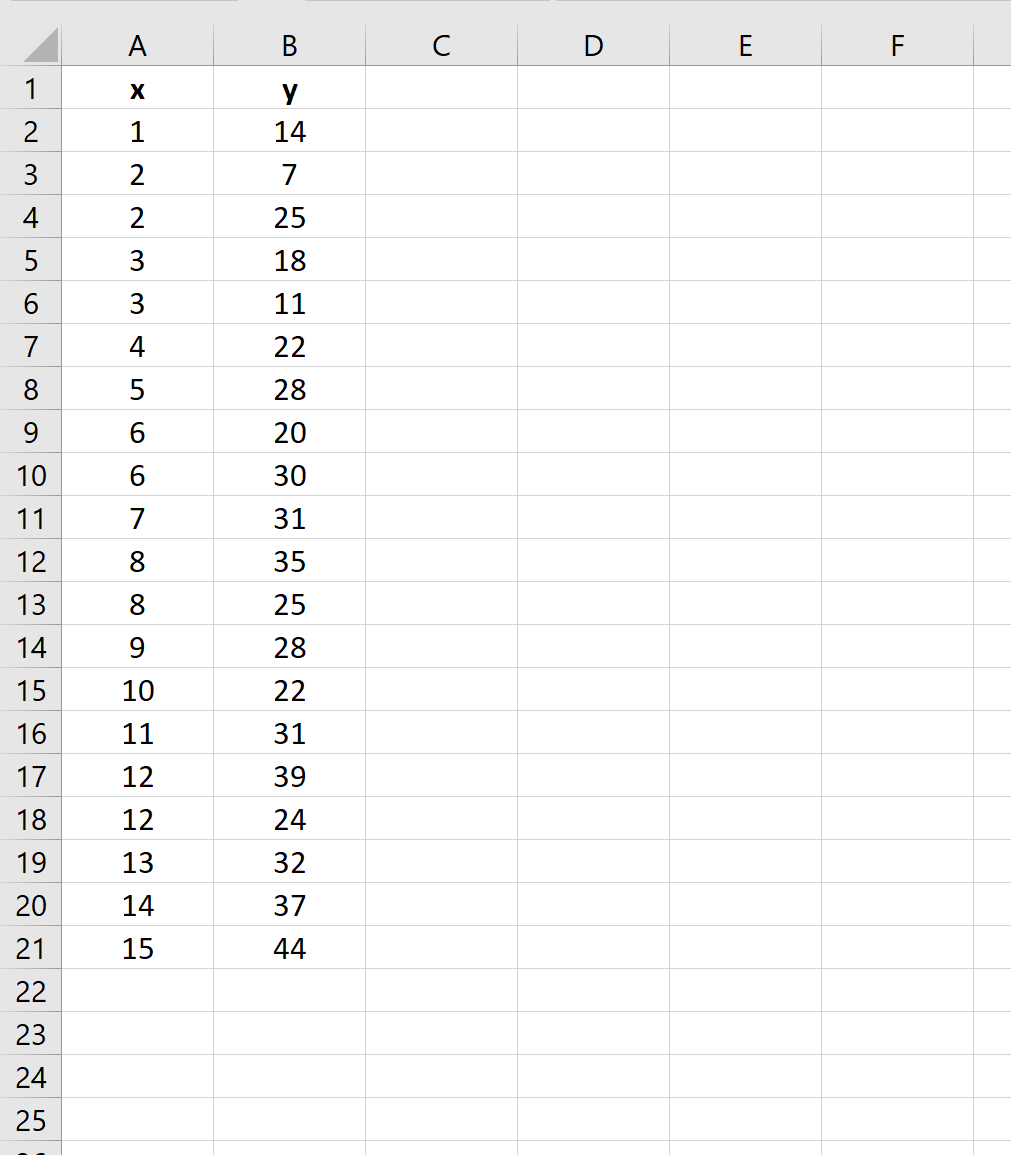
Passo 1: Insira os dados
Primeiro, insira os valores do conjunto de dados:
Etapa 2: realizar regressão linear
Em seguida, clique na guia Dados na faixa superior. Em seguida, clique na opção Análise de Dados no grupo Analisar .

Se você não vir essa opção, primeiro deverá carregar o Analysis ToolPak .
Na nova janela que aparece, clique em Regressão e depois clique em OK .
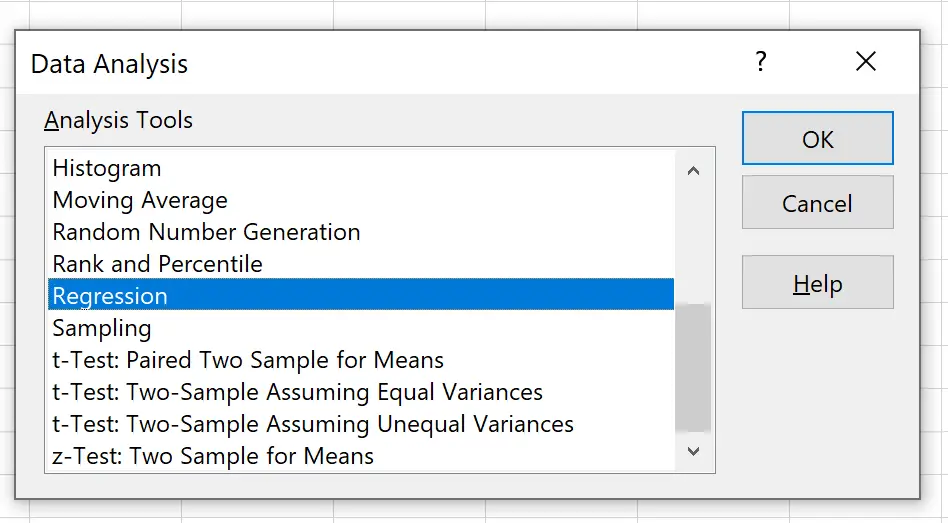
Na nova janela que aparece, forneça as seguintes informações:
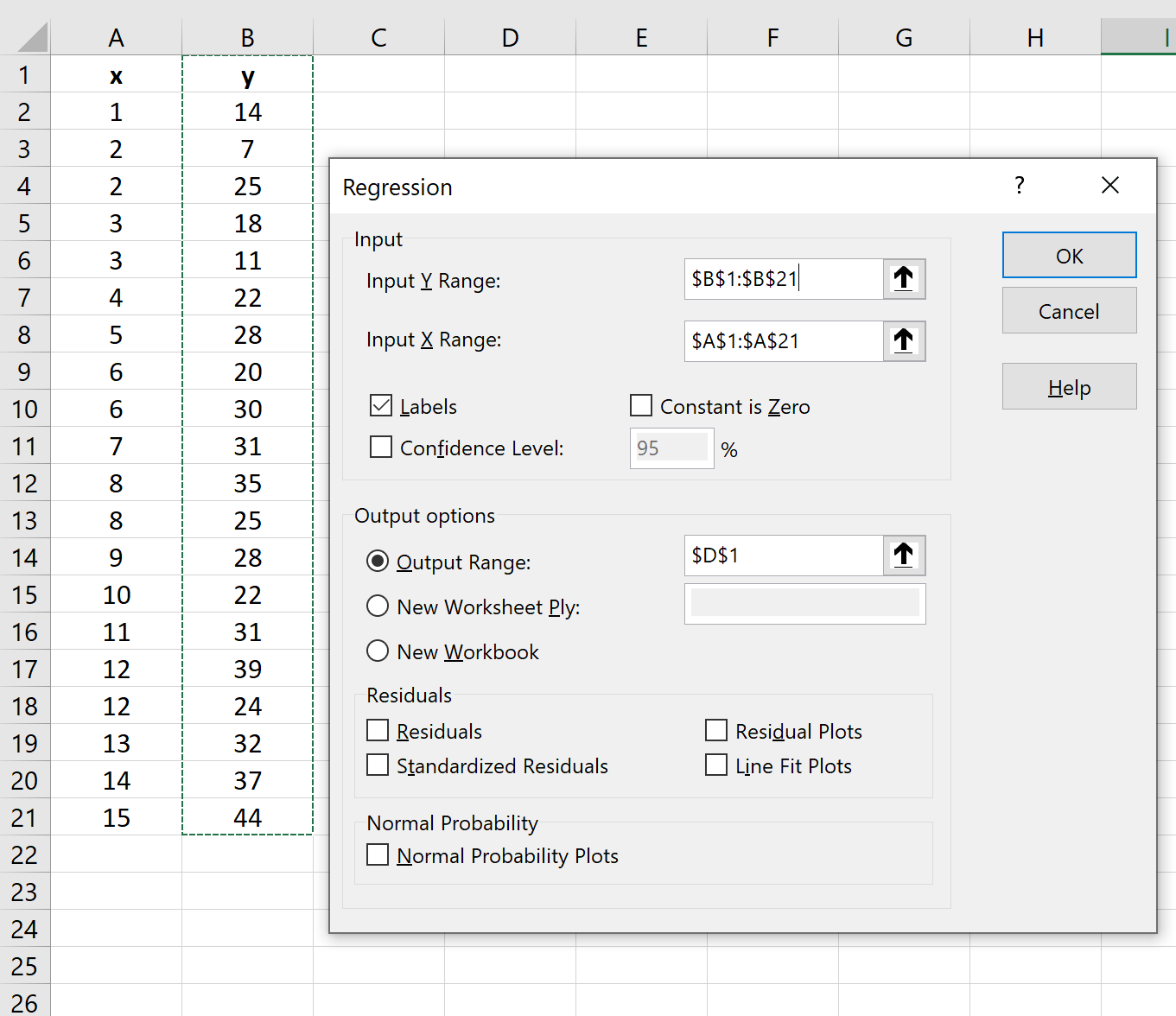
Depois de clicar em OK , o resultado da regressão aparecerá:
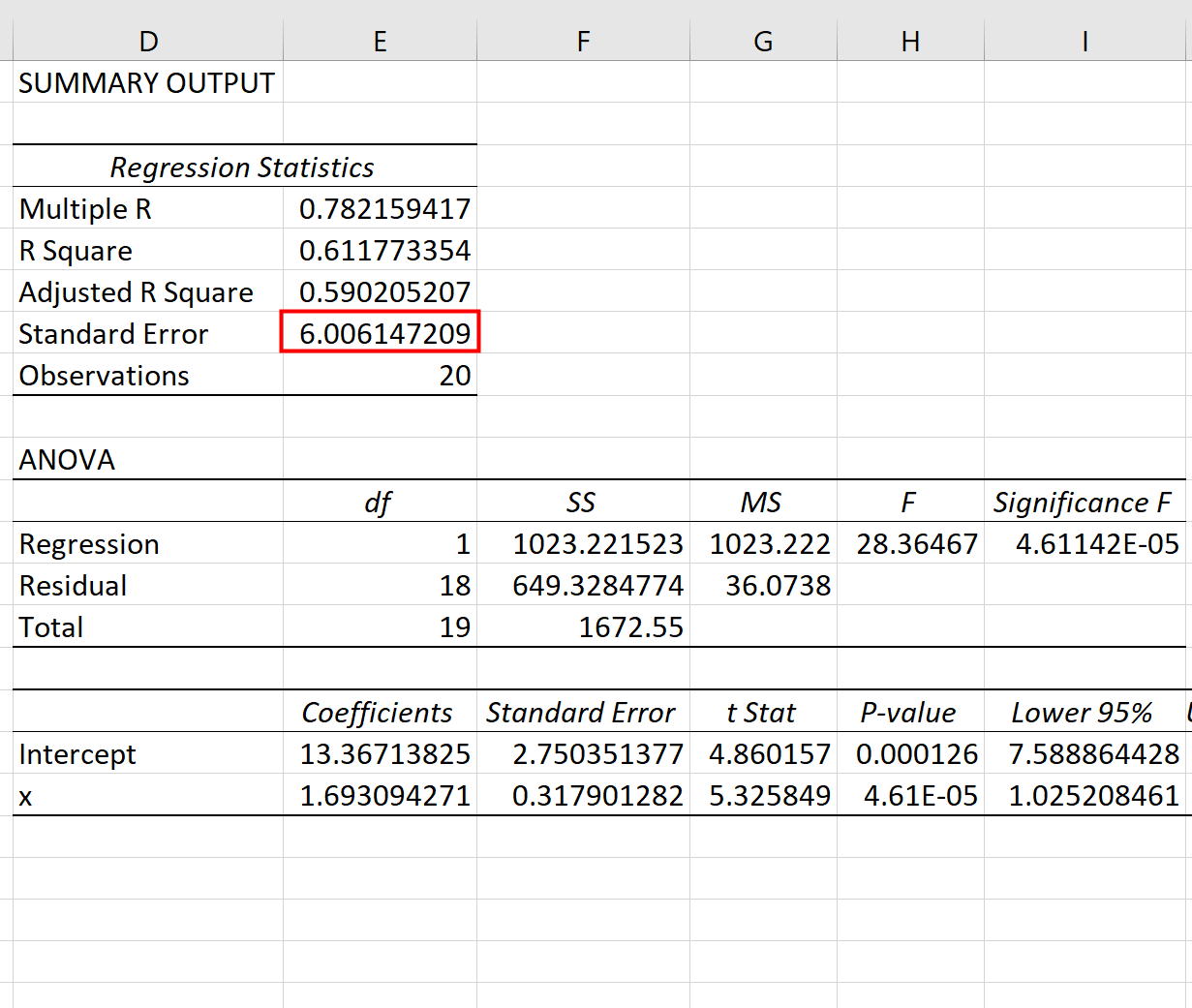
Podemos usar os coeficientes da tabela de regressão para construir a equação de regressão estimada:
ŷ = 13,367 + 1,693(x)
E podemos ver que o erro padrão da estimativa para este modelo de regressão é 6,006 . Em termos simples, isso nos diz que o ponto de dados médio está a 6,006 unidades de distância da linha de regressão.
Podemos usar a equação de regressão estimada e o erro padrão da estimativa para construir um intervalo de confiança de 95% para o valor previsto de um determinado ponto de dados.
Por exemplo, suponha que x seja igual a 10. Usando a equação de regressão estimada, preveríamos que y seria igual a:
ŷ = 13,367 + 1,693*(10) = 30,297
E podemos obter o intervalo de confiança de 95% para esta estimativa usando a seguinte fórmula:
- IC 95% = [ŷ – 1,96*σ é , ŷ + 1,96*σ é ]
Para o nosso exemplo, o intervalo de confiança de 95% seria calculado como:
- IC 95% = [ŷ – 1,96*σ é , ŷ + 1,96*σ é ]
- IC 95% = [30,297 – 1,96*6,006, 30,297 + 1,96*6,006]
- IC 95% = [18.525, 42.069]
Recursos adicionais
Como realizar regressão linear simples no Excel
Como realizar regressão linear múltipla no Excel
Como criar um gráfico residual no Excel