O que é um espaço amostral? definição e exemplos

O espaço amostral de um experimento é o conjunto de todos os resultados possíveis do experimento.

Por exemplo, suponha que lançamos um dado uma vez. O espaço amostral de resultados possíveis inclui:

Espaço amostral = 1, 2, 3, 4, 5, 6

Usando a notação, escrevemos o símbolo do espaço amostral como um S cursivo e os resultados entre parênteses como segue:

S = {1, 2, 3, 4, 5, 6}

Exemplos de espaços amostrais

Aqui estão alguns exemplos adicionais de espaços amostrais:

Exemplo 1: sorteio

Suponha que joguemos uma moeda uma vez. Se deixarmos H = a moeda cair em cara e T = a moeda cair em coroa, então o espaço amostral para este lançamento de moeda é:

S = {H, T}

Exemplo 2: bolinhas de gude em um saco

Suponha que selecionamos aleatoriamente uma bolinha de gude de um saco contendo três bolinhas de gude: uma bolinha de gude vermelha, uma bolinha de gude verde e uma bolinha de gude azul. Se deixarmos R = vermelho, G = verde e B = azul, então o espaço amostral é:

S = {R, G, B}

Exemplo 3: lançamento de moeda e lançamento de dados

Suponha que joguemos uma moeda e lançamos um dado ao mesmo tempo. Se deixarmos H1 representar o resultado de uma “Cabeça” e um “1”, então o espaço amostral para os resultados é:

S = {H1, H2, H3, H4, H5, H6, T1, T2, T3, T4, T5, T6}

O princípio fundamental da contagem

O princípio fundamental da contagem é uma forma de calcular o número total de resultados potenciais de um experimento.

Este princípio afirma que se o evento A tiver n resultados distintos e o evento B tiver m resultados distintos, então o número total de resultados potenciais pode ser calculado da seguinte forma:

Resultados totais = m * n

Exemplo 1: lançamento de moeda e lançamento de dados

Por exemplo, se jogarmos uma moeda e lançarmos um dado ao mesmo tempo, o número total de resultados no espaço amostral pode ser calculado da seguinte forma:

Resultados totais = (2 maneiras pelas quais uma moeda pode cair) * (6 maneiras pelas quais um dado pode cair) = 12 resultados possíveis.

Escrevemos esses 12 resultados no exemplo anterior:

S = {H1, H2, H3, H4, H5, H6, T1, T2, T3, T4, T5, T6}

Exemplo 2: Contando combinações de roupas

Este princípio também pode ser usado para calcular resultados totais em um espaço amostral para mais de dois eventos.

Por exemplo, suponha que uma gaveta aleatória contenha 3 camisas diferentes, 4 calças diferentes e 2 meias diferentes. Se selecionarmos aleatoriamente uma peça de roupa sem olhar, o número total de roupas possíveis seria calculado da seguinte forma:

Total de looks = 3 * 4 * 2 = 24 looks possíveis

Visualizando espaços amostrais com diagramas de árvore

Quando o número de resultados em um espaço amostral é grande, pode ser útil construir um diagrama em árvore para visualizar as diferentes combinações de resultados.

Por exemplo, suponha que um armário contenha 2 camisas diferentes, 2 calças diferentes e 2 meias diferentes. Se selecionarmos aleatoriamente uma peça de roupa sem olhar, o número total de roupas possíveis poderia ser visualizado da seguinte forma:

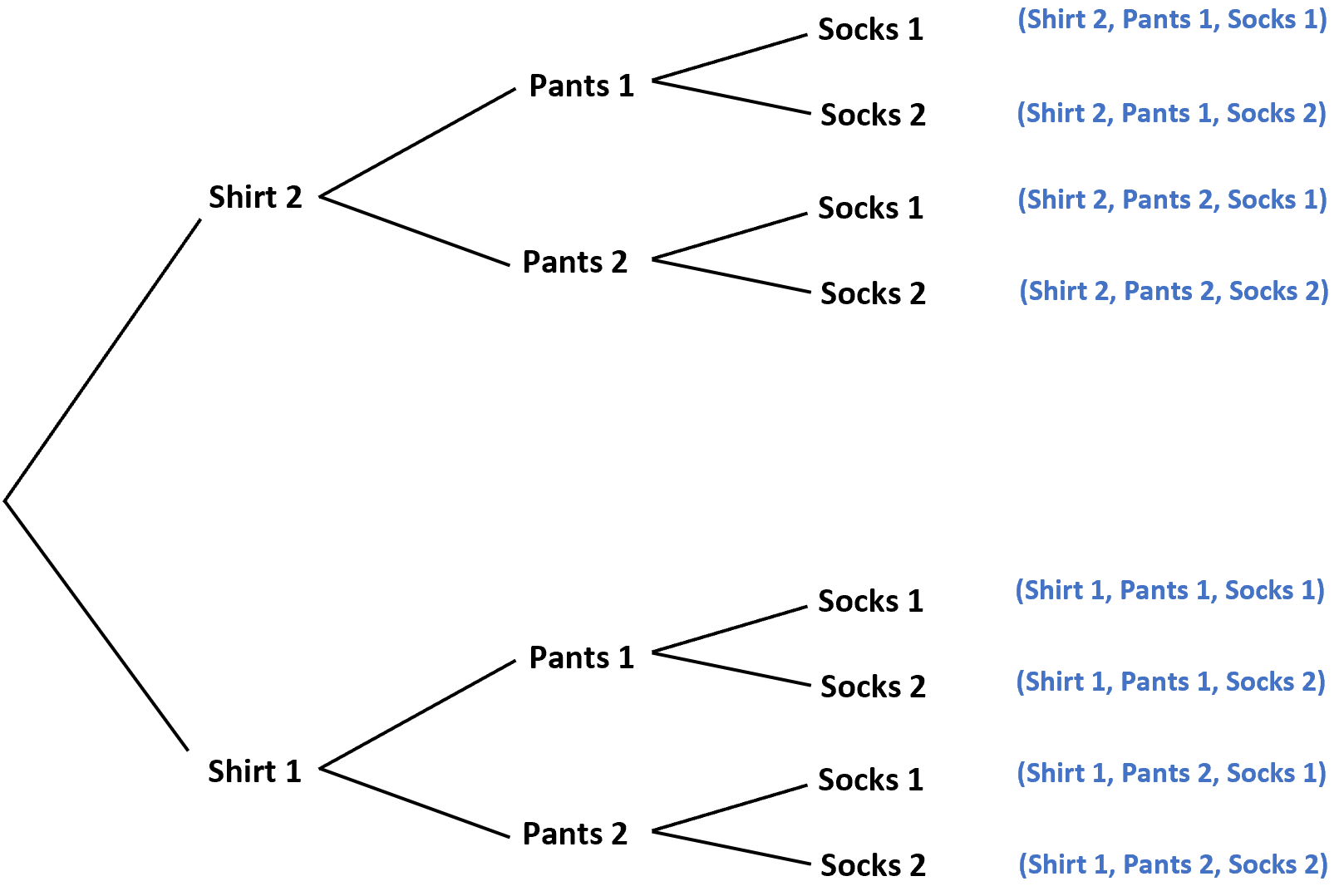
Este diagrama nos ajuda a visualizar os oito resultados potenciais diferentes no espaço amostral.

Também podemos utilizar o princípio fundamental da contagem para confirmar que deve haver oito resultados diferentes:

Resultados totais = 2 camisas * 2 calças * 2 meias = 8 looks possíveis

Calculando probabilidades de resultados em espaços amostrais

Depois de identificarmos o espaço amostral de um experimento, podemos calcular a probabilidade de ocorrência do evento A usando a seguinte fórmula:

P(A) = (Espaço amostral de A) / (Espaço amostral total)

Por exemplo, suponha que lançamos um dado uma vez. O espaço amostral pode ser escrito na forma:

S = {1, 2, 3, 4, 5, 6}

Se definirmos o evento A como o número “2”, então o espaço amostral do evento A pode ser escrito da seguinte forma:

S = {2}

Assim, a probabilidade de ocorrência do evento A pode ser calculada da seguinte forma:

P(UMA) = 1/6

Se definirmos o evento A como o dado caindo em um número par, então o espaço amostral do evento A pode ser escrito da seguinte forma:

S = {2, 4, 6}

Assim, a probabilidade de ocorrência do evento A pode ser calculada da seguinte forma:

P(UMA) = 3/6