Como realizar regressão linear simples no stata

A regressão linear simples é um método que você pode usar para compreender a relação entre uma variável explicativa, x, e uma variável de resposta, y.

Este tutorial explica como realizar uma regressão linear simples no Stata.

Exemplo: Regressão Linear Simples em Stata

Suponha que queiramos entender a relação entre o peso de um carro e sua quilometragem por galão. Para explorar essa relação, podemos realizar uma regressão linear simples usando o peso como variável explicativa e milhas por galão como variável de resposta.

Conclua as etapas a seguir no Stata para realizar uma regressão linear simples usando o conjunto de dados chamado auto , que contém dados de 74 carros diferentes.

Etapa 1: carregar dados.

Carregue os dados digitando o seguinte na caixa de comando:

use https://www.stata-press.com/data/r13/auto

Etapa 2: obtenha um resumo dos dados.

Obtenha uma compreensão rápida dos dados com os quais você está trabalhando digitando o seguinte na caixa Comando:

resumir

Podemos ver que existem 12 variáveis diferentes no conjunto de dados, mas as únicas duas que nos interessam são mpg e peso .

Etapa 3: visualize os dados.

Antes de realizar uma regressão linear simples, vamos primeiro criar um gráfico de dispersão de peso versus mpg para que possamos visualizar a relação entre essas duas variáveis e verificar se há valores discrepantes óbvios. Digite o seguinte na caixa Comando para criar um gráfico de dispersão:

dispersão de peso mpg

Isso produz o seguinte gráfico de dispersão:

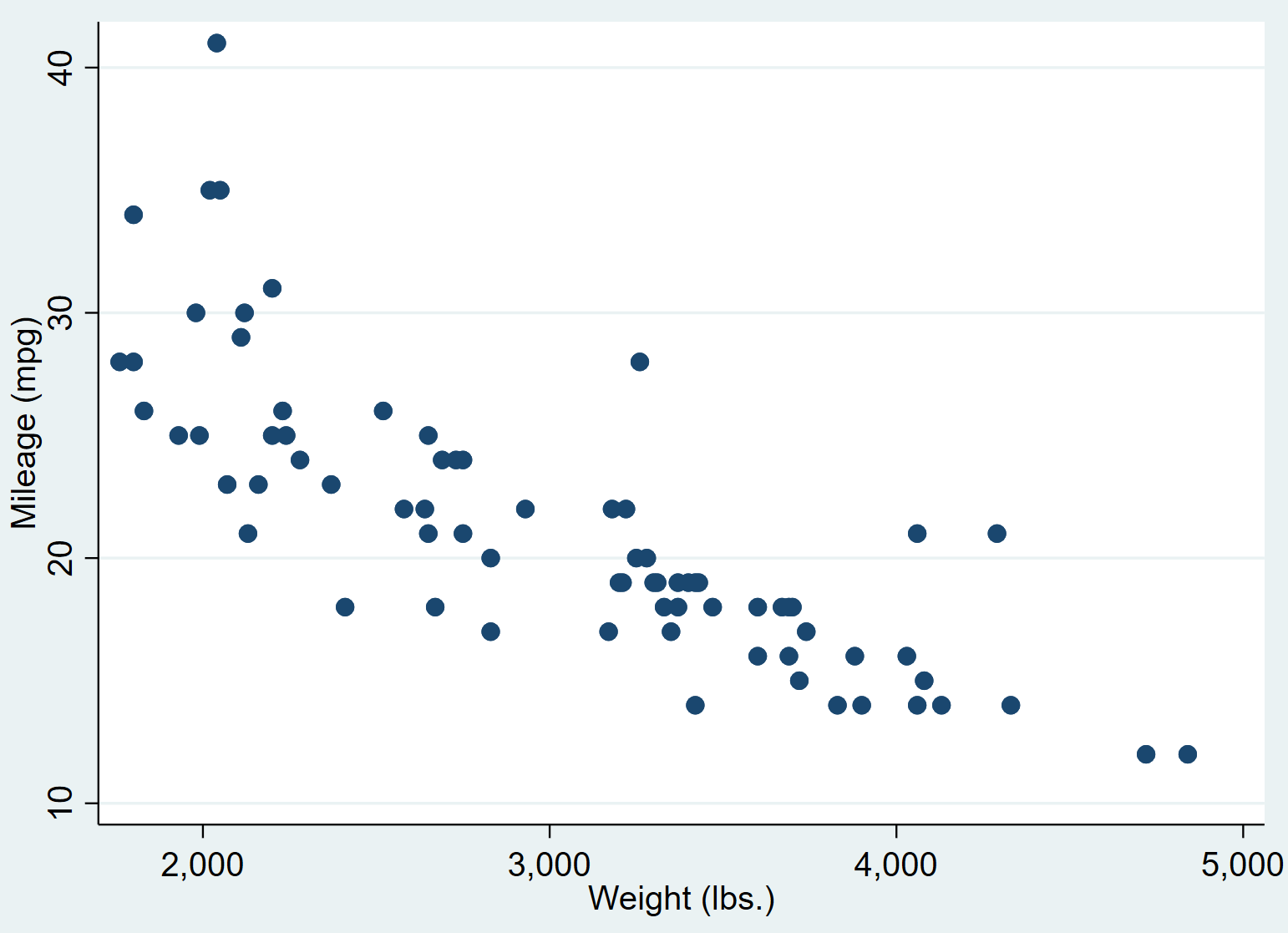
Podemos ver que carros com pesos maiores tendem a ter menos milhas por galão. Para quantificar esta relação, realizaremos agora uma regressão linear simples.

Etapa 4: execute uma regressão linear simples.

Digite o seguinte na caixa Comando para realizar uma regressão linear simples usando peso como variável explicativa e mpg como variável de resposta.

regredir peso para mpg

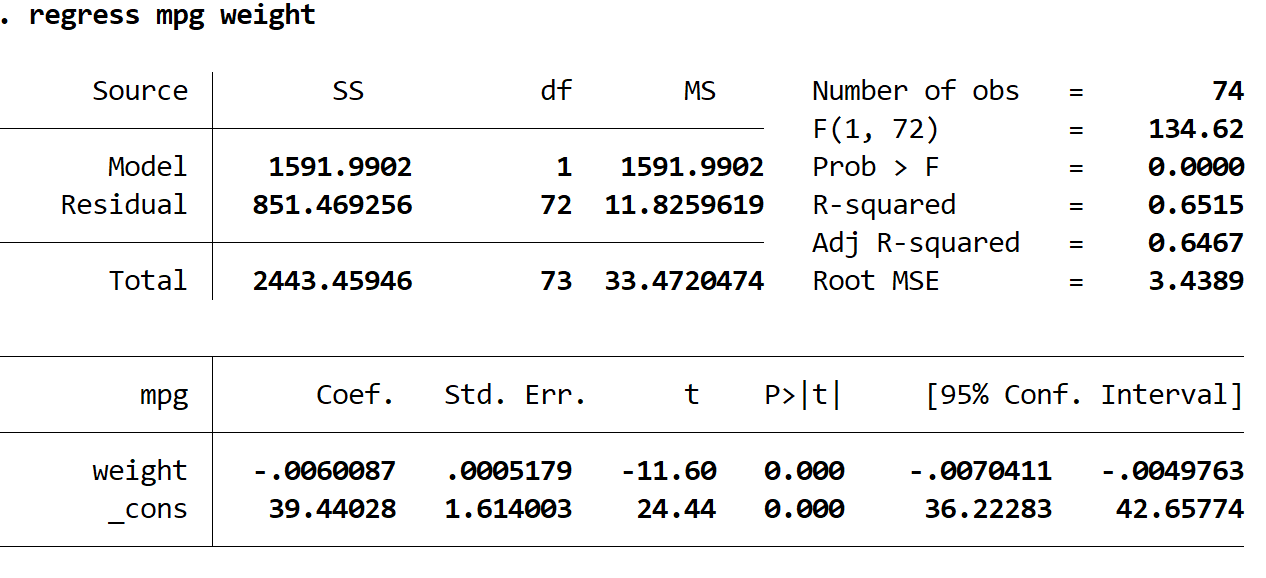
Veja como interpretar os números mais interessantes no resultado:

R ao quadrado: 0,6515. Esta é a proporção da variância na variável resposta que pode ser explicada pela variável explicativa. Neste exemplo, 65,15% da variação do mpg pode ser explicada pelo peso.

Coef (peso): -0,006. Isto nos diz a mudança média na variável de resposta associada a um aumento de uma unidade na variável explicativa. Neste exemplo, cada aumento de meio quilo no peso está associado a uma diminuição de 0,006 mpg em média.

Coef (_cons): 39,44028. Isso nos diz o valor médio da variável resposta quando a variável explicativa é zero. Neste exemplo, o mpg médio é 39,44028 quando o peso de um carro é zero. Realmente não faz sentido interpretar isso, já que o peso de um carro não pode ser zero, mas o número 39,44028 é necessário para formar uma equação de regressão.

P>|t| (peso): 0,000. Este é o valor p associado à estatística de teste de peso. Neste caso, como este valor é inferior a 0,05, podemos concluir que existe uma relação estatisticamente significativa entre peso e mpg.

Equação de regressão: Finalmente, podemos formar uma equação de regressão usando os dois valores dos coeficientes. Neste caso, a equação seria:

mpg previsto = 39,44028 – 0,0060087*(peso)

Podemos utilizar esta equação para determinar o mpg esperado para um carro, dado o seu peso. Por exemplo, um carro que pesa 4.000 libras deve ter um mpg de 15.405:

mpg previsto = 39,44028 – 0,0060087*(4000) = 15,405

Etapa 5: Relate os resultados.

Finalmente, queremos relatar os resultados da nossa regressão linear simples. Aqui está um exemplo de como fazer isso:

Uma regressão linear foi realizada para quantificar a relação entre o peso de um carro e suas milhas por galão. Uma amostra de 74 carros foi utilizada na análise.

Os resultados mostraram que houve uma relação estatisticamente significativa entre peso e mpg (t = -11,60, p <0,0001) e que o peso foi responsável por 65,15% da variabilidade explicada em mpg.

A equação de regressão acabou sendo:

mpg previsto = 39,44 – 0,006 (peso)

Cada libra adicional foi associada a uma diminuição, em média, de -0,006 milhas por galão.