O que é uma estatística de teste padronizada?
Uma hipótese estatística é uma suposição sobre um parâmetro populacional . Por exemplo, podemos assumir que a altura média de um homem nos Estados Unidos é de 70 polegadas. A hipótese relativa à altura é a hipótese estatística e a verdadeira altura média de um homem nos Estados Unidos é o parâmetro populacional .
Um teste de hipótese é um teste estatístico formal que usamos para rejeitar ou não rejeitar uma hipótese estatística.
O processo básico para realizar testes de hipóteses é o seguinte:
1. Colete dados de amostra.
2. Calcule a estatística de teste padronizada para os dados amostrais.
3. Compare a estatística de teste padronizada com um valor crítico. Se for mais extremo que o valor crítico, rejeite a hipótese nula. Caso contrário, não rejeite o teste de hipótese nula.
A fórmula que usamos para calcular a estatística do teste padronizado varia dependendo do tipo de teste de hipótese que estamos realizando.
A tabela a seguir mostra a fórmula a ser usada para calcular a estatística de teste padronizado para cada um dos quatro tipos principais de teste de hipótese:
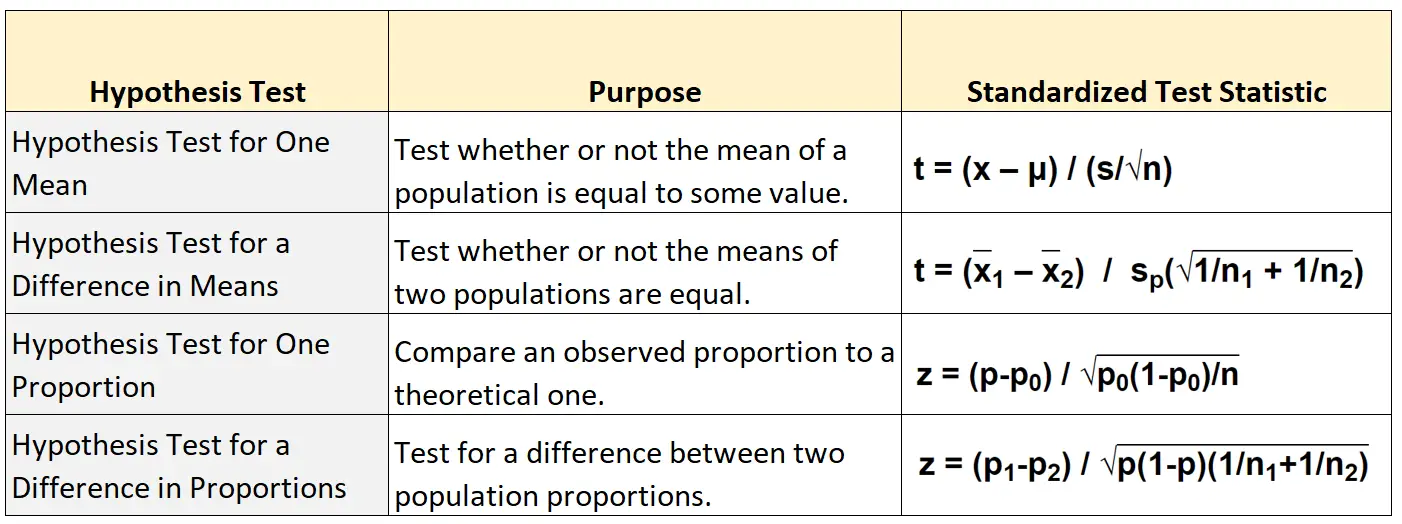
Teste de hipótese para uma média
Um teste t de uma amostra é usado para testar se a média de uma população é ou não igual a um determinado valor.
A estatística de teste padronizada para este tipo de teste é calculada da seguinte forma:
t = ( X – μ) / (s/√n)
Ouro:
- x: média amostral
- μ 0 : média hipotética da população
- s: desvio padrão da amostra
- n: tamanho da amostra
Consulte este tutorial para obter um exemplo de cálculo dessa estatística de teste padronizada.
Teste de hipóteses para uma diferença de médias
Um teste t de duas amostras é usado para testar se as médias de duas populações são iguais ou não.
A estatística de teste padronizada para este tipo de teste é calculada da seguinte forma:
t = ( X 1 – X 2 ) / s p (√ 1/n 1 + 1/n 2 )
onde x 1 ex 2 são as médias amostrais, n 1 e n 2 são os tamanhos amostrais e onde s p é calculado da seguinte forma:
s p = √ (n 1 -1)s 1 2 + (n 2 -1)s 2 2 / (n 1 +n 2 -2)
onde s 1 2 e s 2 2 são as variâncias da amostra.
Consulte este tutorial para obter um exemplo de cálculo dessa estatística de teste padronizada.
Teste de hipótese para uma proporção
Um teste z de uma proporção é usado para comparar uma proporção observada com uma proporção teórica.
A estatística de teste padronizada para este tipo de teste é calculada da seguinte forma:
z = (pp 0 ) / √ p 0 (1-p 0 )/n
Ouro:
- p: proporção amostral observada
- p 0 : proporção hipotética da população
- n: tamanho da amostra
Consulte este tutorial para obter um exemplo de cálculo dessa estatística de teste padronizada.
Teste de hipóteses para uma diferença em proporções
Um teste z de duas proporções é usado para testar a diferença entre duas proporções populacionais.
A estatística de teste padronizada para este tipo de teste é calculada da seguinte forma:
z = (p 1 -p 2 ) / √ p(1-p)(1/n 1 +1/n 2 )
onde p 1 e p 2 são as proporções da amostra, n 1 e n 2 são os tamanhos das amostras e onde p é a proporção total agrupada calculada da seguinte forma:
p = (p 1 n 1 + p 2 n 2 )/(n 1 + n 2 )
Consulte este tutorial para obter um exemplo de cálculo dessa estatística de teste padronizada.
About Author
Dr. benjamim anderson
Olá, sou Benjamin, um professor aposentado de estatística que se tornou professor dedicado na Statorials. Com vasta experiência e conhecimento na área de estatística, estou empenhado em compartilhar meu conhecimento para capacitar os alunos por meio de Statorials. Saber mais