Estatística descritiva ou inferencial: qual a diferença?

Existem dois ramos principais no campo das estatísticas:

• Estatísticas descritivas
• Estatística inferencial

Este tutorial explica a diferença entre os dois ramos e por que cada um é útil em determinadas situações.

Estatísticas descritivas

Resumindo, a estatística descritiva visa descrever um conjunto de dados brutos usando estatísticas resumidas, gráficos e tabelas.

As estatísticas descritivas são úteis porque permitem compreender um grupo de dados com muito mais rapidez e facilidade do que apenas observar linhas e mais linhas de valores de dados brutos.

Por exemplo, digamos que temos um conjunto de dados brutos mostrando as notas dos testes de 1.000 alunos em uma determinada escola. Podemos estar interessados na pontuação média dos testes, bem como na distribuição das pontuações dos testes.

Usando estatísticas descritivas, poderíamos encontrar a pontuação média e criar um gráfico que nos ajudasse a visualizar a distribuição das pontuações.

Isso nos permite entender as pontuações dos testes dos alunos com muito mais facilidade do que apenas olhar os dados brutos.

Formas comuns de estatística descritiva

Existem três formas comuns de estatística descritiva:

1. Estatísticas resumidas. Estas são estatísticas que resumem os dados usando um único número. Existem dois tipos comuns de estatísticas resumidas:

• Medidas de tendência central : Esses números descrevem onde está o centro de um conjunto de dados. Exemplos incluem média   e a mediana .
• Medidas de dispersão: Esses números descrevem a distribuição dos valores no conjunto de dados. Os exemplos incluem intervalo , intervalo interquartil , desvio padrão e variância .

2. Gráficos . Os gráficos nos ajudam a visualizar os dados. Tipos comuns de gráficos usados para visualizar dados incluem gráficos de caixa , histogramas , gráficos de caule e folhas e gráficos de dispersão .

3. Tabelas . As tabelas podem nos ajudar a entender como os dados são distribuídos. Um tipo comum de tabela é a tabela de frequência , que nos informa quantos valores de dados estão dentro de determinados intervalos.

Exemplo de uso de estatística descritiva

O exemplo a seguir ilustra como podemos usar estatísticas descritivas no mundo real.

Suponha que 1.000 alunos de uma determinada escola façam o mesmo teste. Queremos entender a distribuição dos resultados dos testes, por isso usamos as seguintes estatísticas descritivas:

1. Estatísticas resumidas

Média: 82,13 . Isso nos diz que a pontuação média do teste entre os 1.000 alunos é 82,13.

Mediana: 84. Isso nos diz que metade de todos os alunos obteve pontuação acima de 84 e a outra metade obteve pontuação abaixo de 84.

Máx: 100. Mín: 45. Isso nos diz que a pontuação máxima obtida por qualquer aluno foi 100 e a pontuação mínima foi 45. O intervalo – que nos indica a diferença entre o máximo e o mínimo – é 55.

2. Gráficos

Para visualizar a distribuição dos resultados dos testes, podemos criar um histograma – um tipo de gráfico que utiliza barras retangulares para representar frequências.

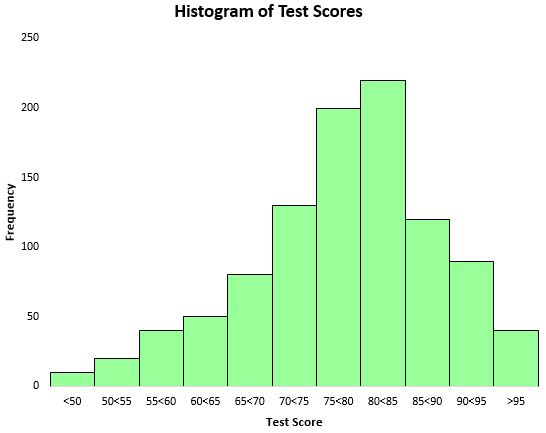
Com base neste histograma, podemos ver que a distribuição das pontuações dos testes tem aproximadamente a forma de um sino. A maioria dos alunos obteve pontuações entre 70 e 90, enquanto muito poucos obtiveram pontuações acima de 95 e menos ainda obtiveram pontuações abaixo de 50.

3. Tabelas

Outra maneira fácil de entender a distribuição das pontuações é criar uma tabela de frequência. Por exemplo, a tabela de frequência a seguir mostra a porcentagem de alunos que pontuaram entre diferentes faixas:

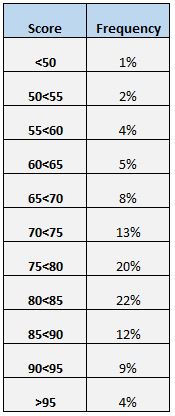
Podemos ver que apenas 4% do total de alunos pontuaram acima de 95. Também podemos ver que (12% + 9% + 4% =) 25% de todos os alunos pontuaram 85 ou mais.

Uma tabela de frequência é particularmente útil se quisermos saber qual porcentagem dos valores dos dados está acima ou abaixo de um determinado valor. Por exemplo, suponha que a escola considere uma pontuação “aceitável” no teste como qualquer pontuação acima de 75.

Observando a tabela de frequências, podemos facilmente perceber que (20% + 22% + 12% + 9% + 4% = ) 67% dos alunos obtiveram nota aceitável na prova.

Estatística inferencial

Em suma, a estatística inferencial utiliza uma pequena amostra de dados para tirar conclusões sobre a população maior da qual a amostra é extraída.

Por exemplo, podemos querer compreender as preferências políticas de milhões de pessoas num país.

No entanto, seria muito demorado e dispendioso entrevistar todos os indivíduos do país. Assim, em vez disso, faríamos um inquérito mais pequeno, digamos, a 1.000 americanos, e utilizaríamos os resultados do inquérito para tirar conclusões sobre a população como um todo.

Esta é toda a premissa da estatística inferencial: queremos responder a uma questão sobre uma população, por isso obtemos dados para uma pequena amostra dessa população e utilizamos os dados da amostra para fazer inferências sobre a população.

A importância de uma amostra representativa

Para ter confiança na nossa capacidade de usar uma amostra para tirar conclusões sobre uma população, devemos garantir que temos uma amostra representativa , ou seja, uma amostra na qual as características dos indivíduos da população A amostra corresponde de perto à amostra características. da população em geral.

Idealmente, queremos que a nossa amostra se assemelhe a uma “miniversão” da nossa população. Assim, se quisermos tirar conclusões sobre uma população de estudantes composta por 50% de meninas e 50% de meninos, nossa amostra não seria representativa se incluísse 90% de meninos e apenas 10% de meninas.

Se a nossa amostra não for semelhante à população em geral, não podemos generalizar com segurança os resultados da amostra para a população em geral.

Como obter uma amostra representativa

Para maximizar as chances de obter uma amostra representativa, você deve se concentrar em duas coisas:

1. Certifique-se de usar um método de amostragem aleatória.

Existem vários métodos de amostragem aleatória que você pode usar e que provavelmente produzirão uma amostra representativa, incluindo:

• Uma amostra aleatória simples
• Uma amostra aleatória sistemática
• Uma amostra aleatória de cluster
• Uma amostra aleatória estratificada

Os métodos de amostragem aleatória tendem a produzir amostras representativas porque cada membro da população tem chances iguais de ser incluído na amostra.

2. Certifique-se de que o tamanho da sua amostra seja grande o suficiente .

Além de usar um método de amostragem apropriado, é importante garantir que a amostra seja grande o suficiente para que você tenha dados suficientes para poder generalizar para uma população maior.

Para determinar o tamanho da sua amostra, você precisa considerar o tamanho da população que está estudando, o nível de confiança que deseja usar e a margem de erro que considera aceitável.

Felizmente, você pode usar calculadoras online para inserir esses valores e ver qual deve ser o tamanho da sua amostra.

Formas comuns de estatísticas inferenciais

Existem três formas comuns de estatística inferencial:

1. Teste de hipóteses.

Muitas vezes queremos responder a perguntas sobre uma população como:

• A porcentagem de pessoas em Ohio que apoiam o Candidato A é superior a 50%?
• A altura média de uma determinada planta é igual a 14 polegadas?
• Existe diferença entre a altura média dos alunos da escola A e da escola B?

Para responder a estas questões, podemos realizar testes de hipóteses , o que nos permite utilizar dados de uma amostra para tirar conclusões sobre populações.

2. Intervalos de confiança .

Às vezes queremos estimar um determinado valor para uma população. Por exemplo, podemos estar interessados na altura média de uma determinada espécie de planta na Austrália.

Em vez de medir todas as plantas do país, poderíamos coletar uma pequena amostra de plantas e medir cada uma delas. Então podemos usar a altura média das plantas na amostra para estimar a altura média da população.

No entanto, é improvável que a nossa amostra forneça uma estimativa populacional perfeita. Felizmente, podemos explicar essa incerteza criando um intervalo de confiança , que fornece uma faixa de valores dentro da qual temos certeza de que se encontra o verdadeiro parâmetro populacional.

Por exemplo, poderíamos produzir um intervalo de confiança de 95% de [13,2, 14,8], o que significa que temos 95% de certeza de que a verdadeira altura média desta espécie de planta está entre 13,2 polegadas e 14,8 polegadas.

3. Regressão .

Às vezes queremos compreender a relação entre duas variáveis numa população.

Por exemplo, digamos que queremos saber se as horas gastas estudando por semana estão relacionadas às notas dos testes . Para responder a esta pergunta, poderíamos realizar uma técnica conhecida como análise de regressão .

Assim, podemos olhar a quantidade de horas estudadas bem como as notas dos testes de 100 alunos e realizar uma análise de regressão para ver se existe uma relação significativa entre as duas variáveis.

Se o valor p da regressão for significativo , então podemos concluir que existe uma relação significativa entre essas duas variáveis na população estudantil geral.

A diferença entre estatística descritiva e inferencial

Em resumo, a diferença entre estatística descritiva e inferencial pode ser descrita da seguinte forma:

A estatística descritiva usa estatísticas resumidas, gráficos e tabelas para descrever um conjunto de dados.

Isso é útil para nos ajudar a compreender de forma rápida e fácil um conjunto de dados, sem passar por todos os valores de dados individuais.

A estatística inferencial usa amostras para tirar conclusões sobre populações maiores.

Dependendo da pergunta que você deseja responder sobre uma população, você pode decidir usar um ou mais dos seguintes métodos: teste de hipóteses, intervalos de confiança e análise de regressão.

Se você optar por usar um desses métodos, lembre-se de que sua amostra deve ser representativa de sua população , caso contrário, as conclusões tiradas não serão confiáveis.