Como realizar regressão hierárquica no stata

A regressão hierárquica é uma técnica que podemos usar para comparar vários modelos lineares diferentes.

A ideia básica é que primeiro ajustemos um modelo de regressão linear com uma única variável explicativa. A seguir, ajustamos outro modelo de regressão utilizando uma variável explicativa adicional. Se o R-quadrado (a proporção de variância na variável resposta que pode ser explicada pelas variáveis explicativas) no segundo modelo for significativamente maior do que o R-quadrado no modelo anterior, isso significa que o segundo modelo é melhor.

Em seguida, repetimos o processo de ajuste de modelos de regressão adicionais com mais variáveis explicativas e verificamos se os modelos mais recentes oferecem uma melhoria em relação aos modelos anteriores.

Este tutorial fornece um exemplo de como realizar regressão hierárquica no Stata.

Exemplo: regressão hierárquica no Stata

Usaremos um conjunto de dados integrado chamado auto para ilustrar como realizar a regressão hierárquica no Stata. Primeiro, carregue o conjunto de dados digitando o seguinte na caixa de comando:

uso automático do sistema

Podemos obter um rápido resumo dos dados usando o seguinte comando:

resumir

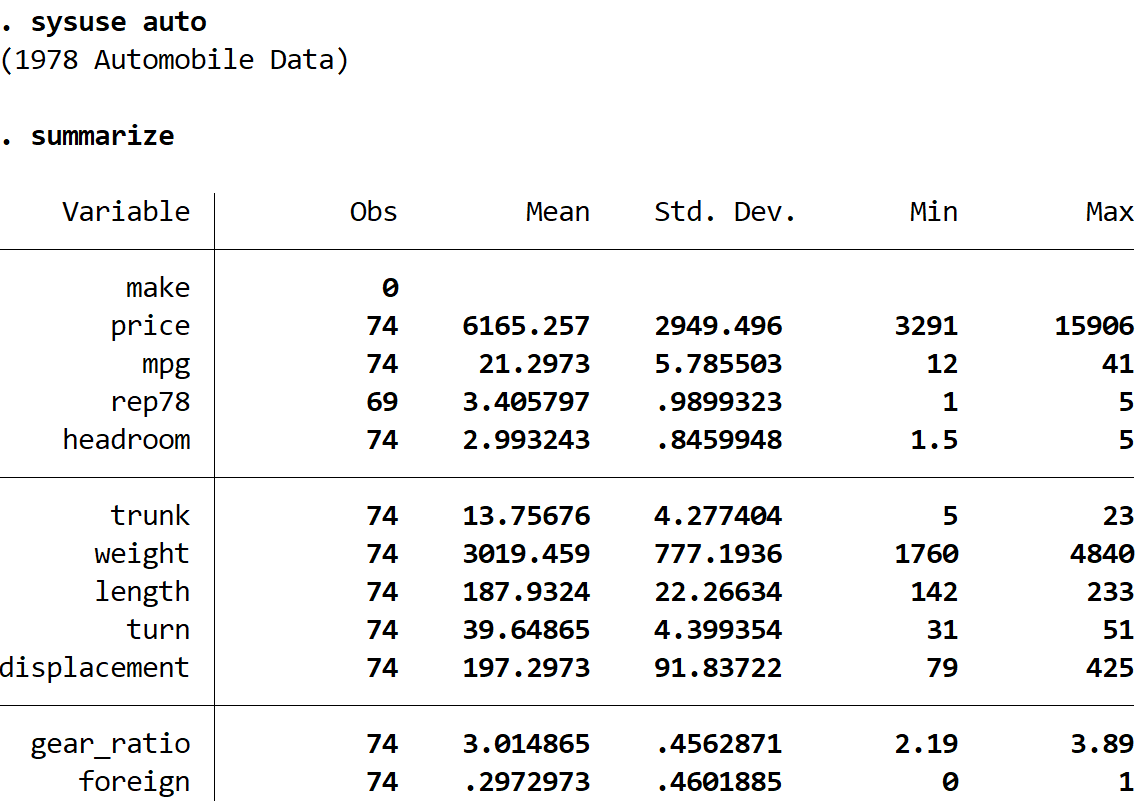
Podemos ver que o conjunto de dados contém informações sobre 12 variáveis diferentes para 74 carros no total.

Ajustaremos os três modelos de regressão linear a seguir e usaremos a regressão hierárquica para ver se cada modelo subsequente fornece ou não uma melhoria significativa em relação ao modelo anterior:

Modelo 1: preço = interceptação + mpg

Modelo 2: preço = interceptação + mpg + peso

Modelo 3: preço = interceptação + mpg + peso + relação de transmissão

Para realizar a regressão hierárquica no Stata, primeiro precisaremos instalar o pacote Hireg . Para fazer isso, digite o seguinte na caixa Comando:

encontrar Hireg

Na janela que aparece, clique em Hireg em https://fmwww.bc.edu/RePEc/bocode/h

Na próxima janela, clique no link que diz clique aqui para instalar .

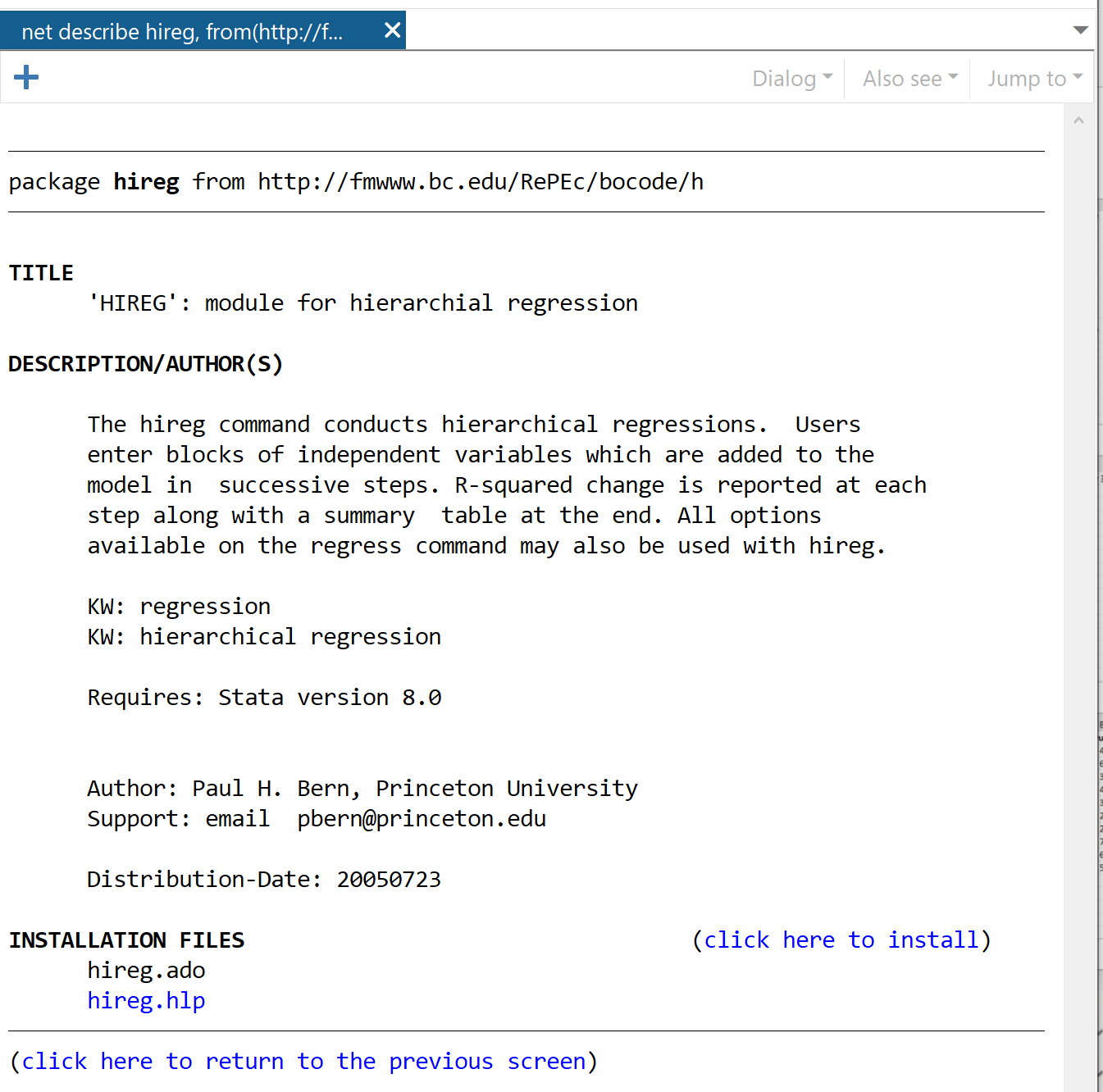
O pacote será instalado em segundos. Então, para realizar uma regressão hierárquica, usaremos o seguinte comando:

preço do aluguel (mpg) (peso) (gear_ratio)

Aqui está o que isso pede ao Stata para fazer:

• Execute uma regressão hierárquica usando o preço como variável de resposta em cada modelo.
• Para o primeiro modelo, use mpg como variável explicativa.
• Para o segundo modelo, adicione peso como variável explicativa adicional.
• Para o terceiro modelo, adicione gear_ratio como outra variável explicativa.

Aqui está o resultado do primeiro modelo:

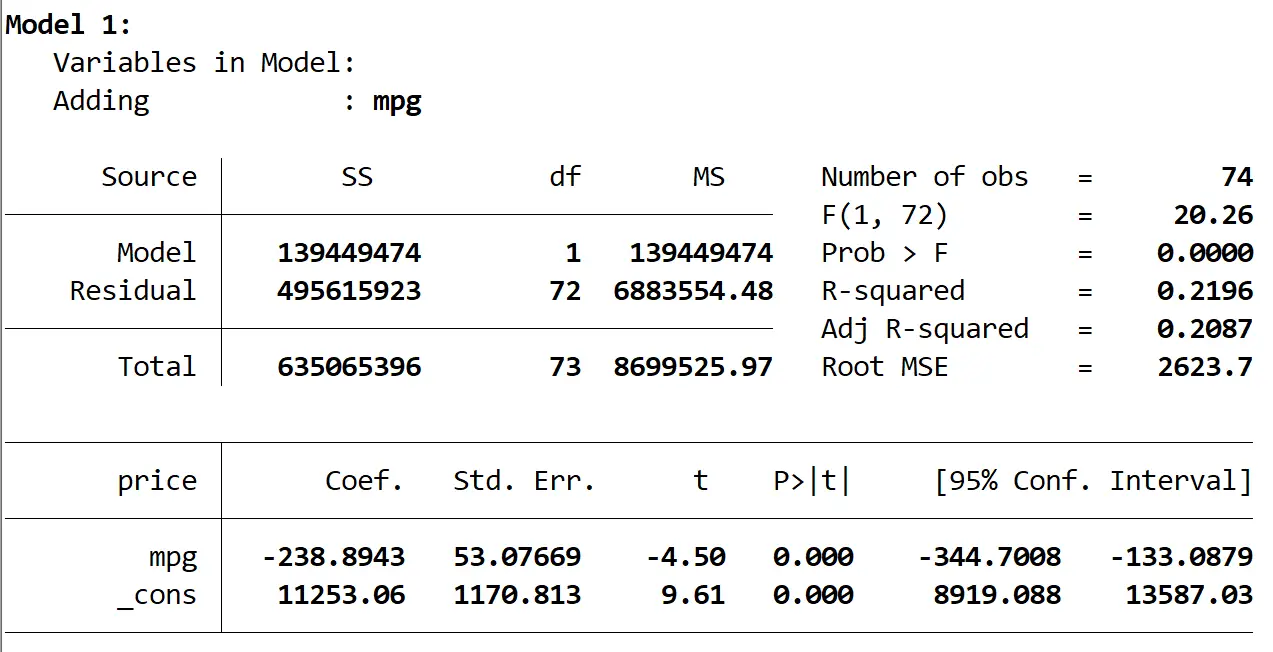
Vemos que o R-quadrado do modelo é 0,2196 e o valor p geral (Prob > F) do modelo é 0,0000 , o que é estatisticamente significativo em α = 0,05.

A seguir, vemos o resultado do segundo modelo:

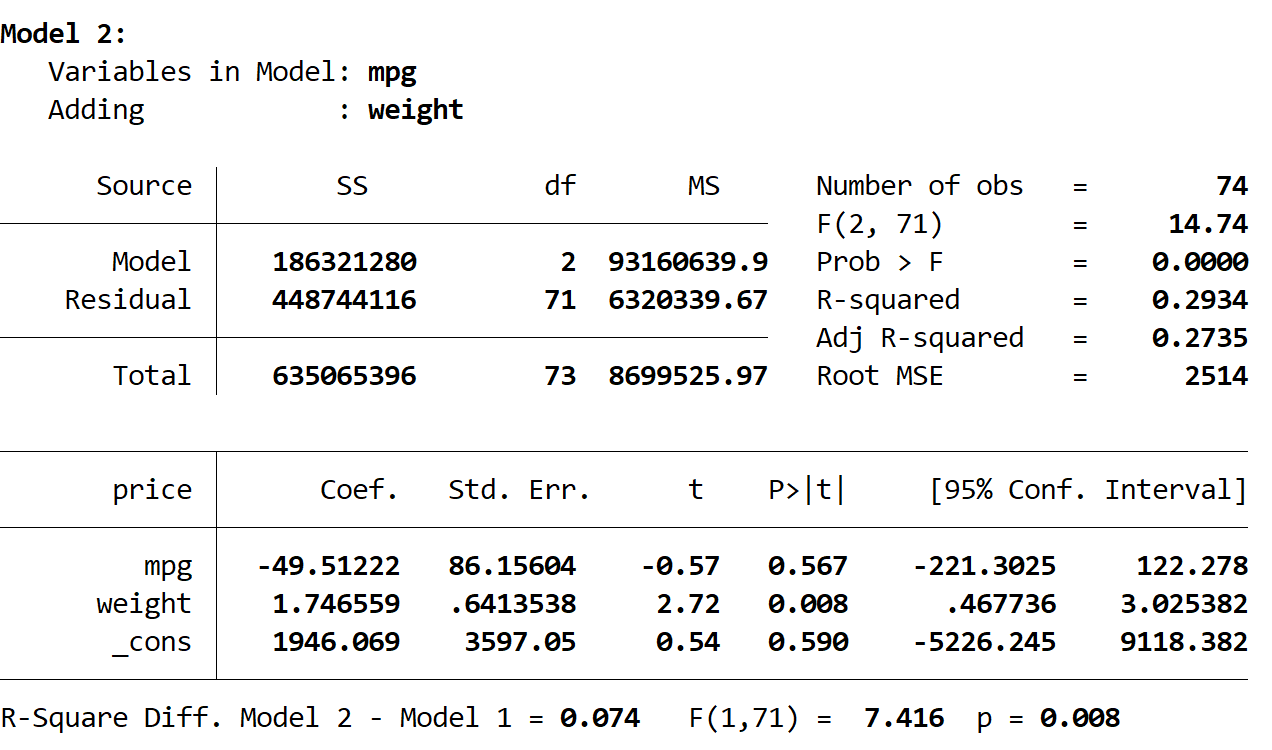
O R quadrado deste modelo é 0,2934 , que é maior que o do primeiro modelo. Para determinar se esta diferença é estatisticamente significativa, o Stata realizou um teste F que deu os seguintes números na parte inferior do resultado:

• Diferença R ao quadrado entre os dois modelos = 0,074
• Estatística F para diferença = 7,416
• Valor p correspondente da estatística F = 0,008

Como o valor p é inferior a 0,05, concluímos que há uma melhoria estatisticamente significativa no segundo modelo em comparação com o primeiro modelo.

Finalmente, podemos ver o resultado do terceiro modelo:

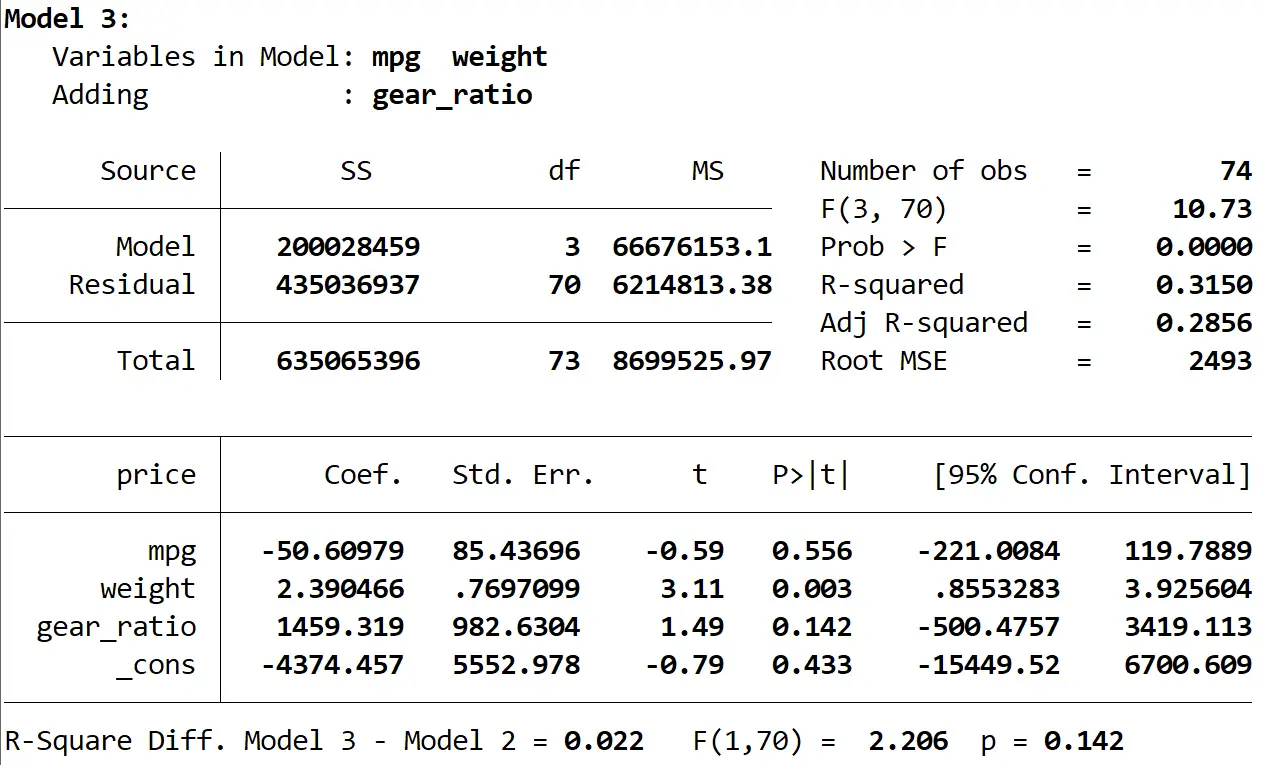
O R quadrado deste modelo é 0,3150 , que é maior que o do segundo modelo. Para determinar se esta diferença é estatisticamente significativa, o Stata realizou um teste F que deu os seguintes números na parte inferior do resultado:

• Diferença R ao quadrado entre os dois modelos = 0,022
• Estatística F para diferença = 2,206
• Valor p correspondente da estatística F = 0,142

Como o valor p não é inferior a 0,05, não temos evidências suficientes para afirmar que o terceiro modelo proporciona uma melhoria em relação ao segundo modelo.

No final do resultado, podemos ver que o Stata fornece um resumo dos resultados:

Neste exemplo específico, concluiríamos que o Modelo 2 ofereceu uma melhoria significativa em relação ao Modelo 1, mas que o Modelo 3 não ofereceu uma melhoria significativa em relação ao Modelo 2.