Como realizar regressão quadrática no stata

Quando duas variáveis têm um relacionamento linear, muitas vezes você pode usar a regressão linear simples para quantificar seu relacionamento.

No entanto, quando duas variáveis têm uma relação quadrática, você pode usar a regressão quadrática para quantificar a sua relação.

Este tutorial explica como realizar regressão quadrática no Stata.

Exemplo: regressão quadrática no Stata

Suponha que queiramos compreender a relação entre o número de horas trabalhadas e a felicidade. Temos os seguintes dados sobre o número de horas trabalhadas por semana e o nível de felicidade relatado (numa escala de 0 a 100) para 16 pessoas diferentes:

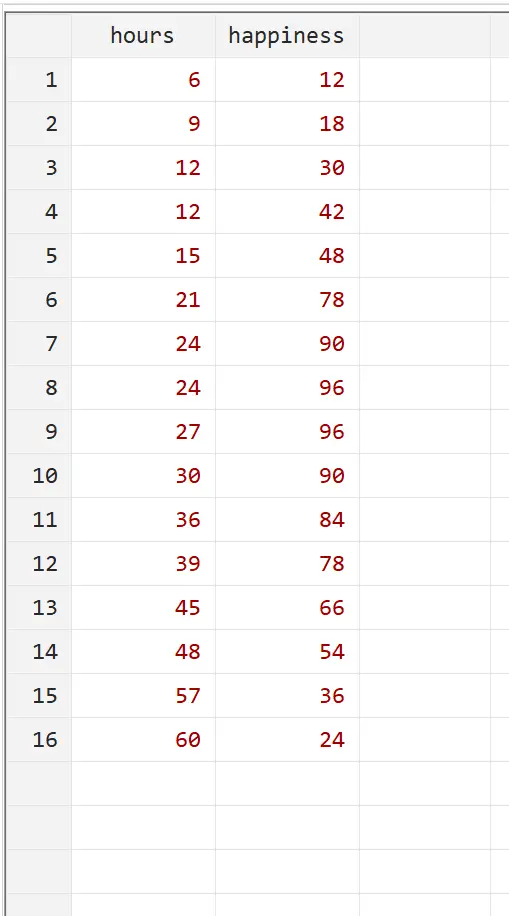
Você pode reproduzir este exemplo inserindo esses dados exatos no Stata usando Dados > Editor de Dados > Editor de Dados (Editar) no menu superior.

Use as etapas a seguir para realizar a regressão quadrática no Stata.

Etapa 1: visualize os dados.

Antes de podermos usar a regressão quadrática, devemos garantir que a relação entre a variável explicativa (horas) e a variável resposta (felicidade) é de fato quadrática. Então, vamos visualizar os dados usando um gráfico de dispersão digitando o seguinte na caixa Comando:

dispersar as horas de felicidade

Isso produz o seguinte gráfico de dispersão:

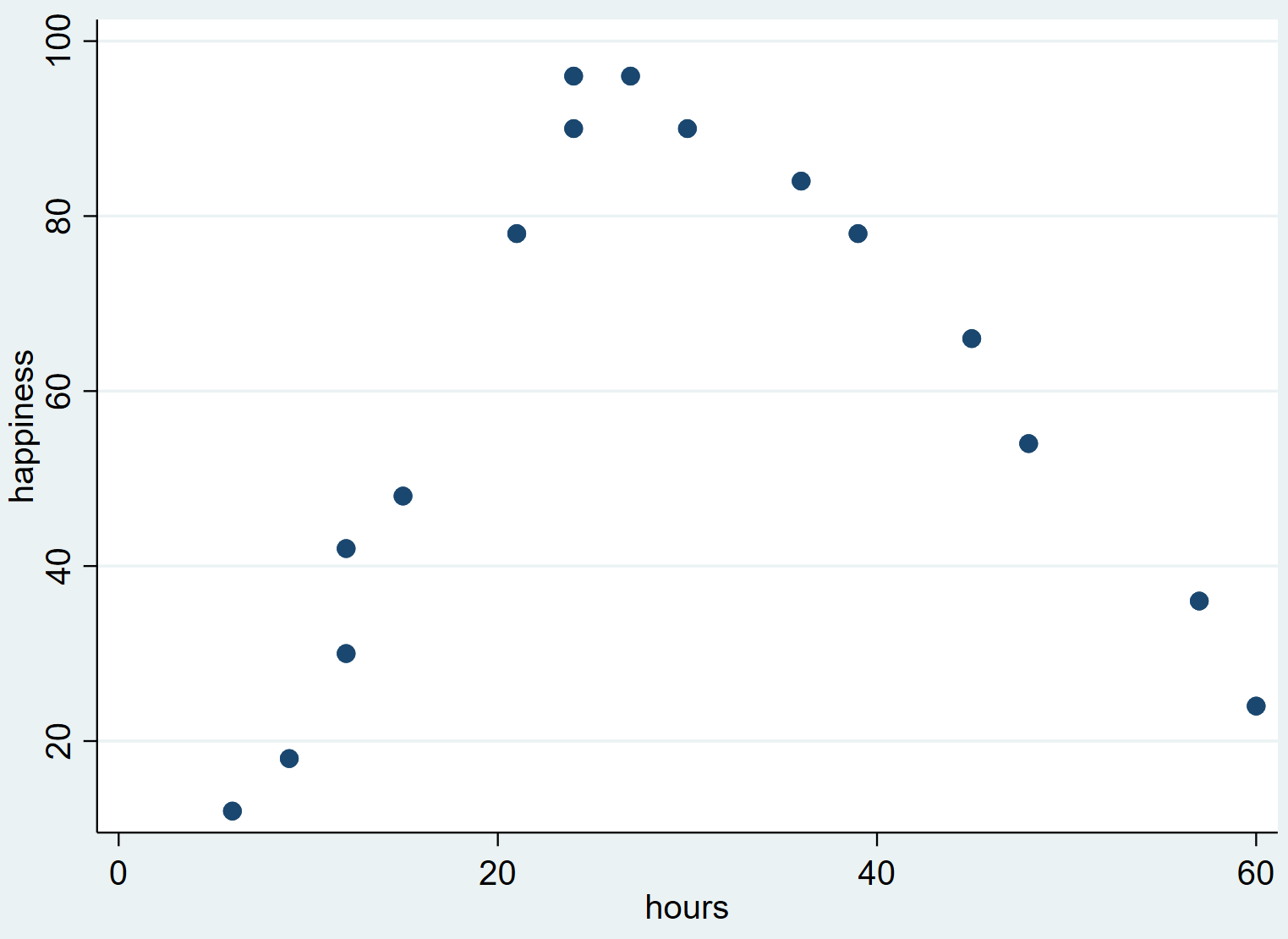
Podemos ver que a felicidade tende a aumentar à medida que o número de horas trabalhadas aumenta de zero até um certo ponto, mas depois começa a diminuir à medida que o número de horas trabalhadas ultrapassa cerca de 30.

Esta forma de “U” invertido no gráfico de dispersão indica que existe uma relação quadrática entre horas trabalhadas e felicidade, o que significa que devemos usar a regressão quadrática para quantificar esta relação.

Etapa 2: execute a regressão quadrática.

Antes de ajustar o modelo de regressão quadrática aos dados, precisamos criar uma nova variável para os valores quadrados de nossa variável preditora de horas . Podemos fazer isso digitando o seguinte na caixa Comando:

gen horas2 = horas*horas

Podemos visualizar esta nova variável acessando Dados > Editor de Dados > Editor de Dados (Navegar) no menu superior.

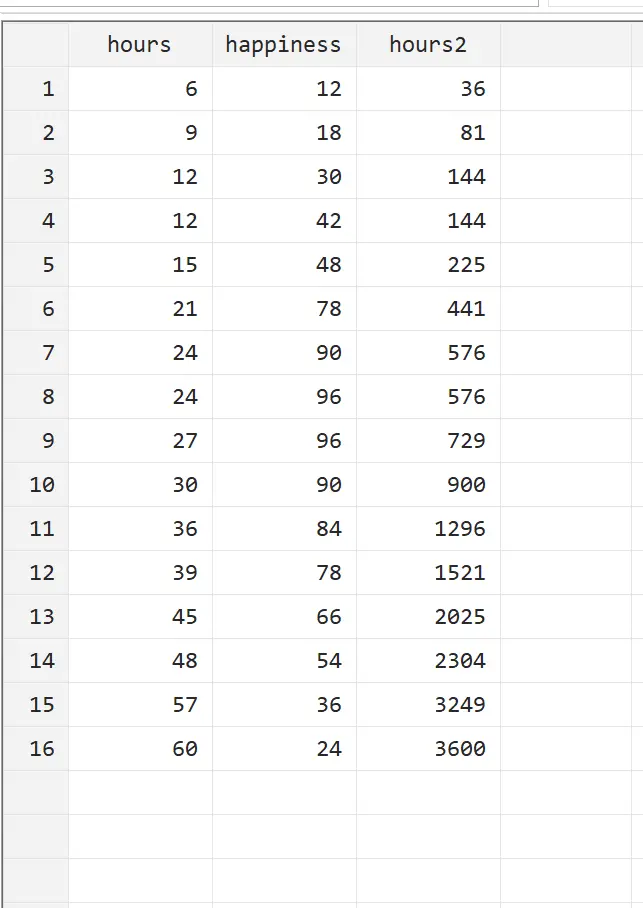
Podemos ver que horas2 é simplesmente horas ao quadrado. Podemos agora realizar uma regressão quadrática usando horas e horas2 como variáveis explicativas e felicidade como variável de resposta. Para realizar uma regressão quadrática, digite o seguinte na caixa Comando:

horas de regressão horas de felicidade horas2

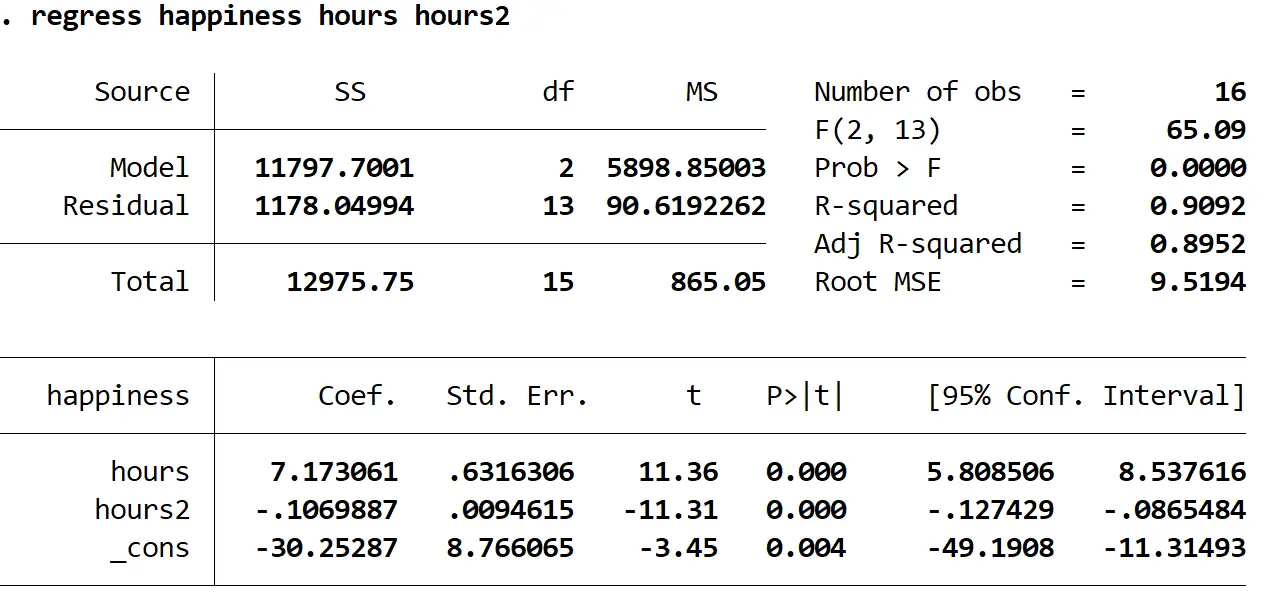
Veja como interpretar os números mais interessantes no resultado:

Prob > F: 0,000. Este é o valor p para a regressão geral. Como esse valor é menor que 0,05, isso significa que as variáveis preditoras horas e horas ² combinadas possuem uma relação estatisticamente significativa com a variável resposta felicidade .

R ao quadrado: 0,9092. Esta é a proporção da variância na variável resposta que pode ser explicada pela variável explicativa. Neste exemplo, 90,92% da variação da felicidade pode ser explicada por horas e horas ² .

Equação de regressão: podemos formar uma equação de regressão usando os valores dos coeficientes mostrados na tabela de saída. Neste caso, a equação seria:

felicidade prevista = -30,25287 + 7,173061 (horas) – 0,1069887 ( ² horas)

Podemos utilizar esta equação para determinar a felicidade prevista de um indivíduo, dado o número de horas que trabalha por semana.

Por exemplo, uma pessoa que trabalha 60 horas por semana deveria ter um nível de felicidade de 14,97:

felicidade prevista = -30,25287 + 7,173061(60) – 0,1069887(60 ² ) = 14,97 .

Por outro lado, uma pessoa que trabalha 30 horas por semana deveria ter um nível de felicidade de 88,65:

felicidade prevista = -30,25287 + 7,173061(30) – 0,1069887(30 ² ) = 88,65 .

Etapa 3: relatar os resultados.

Finalmente, queremos relatar os resultados da nossa regressão quadrática. Aqui está um exemplo de como fazer isso:

Foi realizada uma regressão quadrática para quantificar a relação entre o número de horas que um indivíduo trabalhou e seu correspondente nível de felicidade (medido de 0 a 100). Uma amostra de 16 pessoas foi utilizada na análise.

Os resultados mostraram que houve relação estatisticamente significativa entre as variáveis explicativas horas e horas ² e a variável resposta felicidade (F(2, 13) = 65,09, p < 0,0001).

Juntas, estas duas variáveis explicativas representaram 90,92% da variabilidade explicada na felicidade.

A equação de regressão acabou sendo:

felicidade prevista = -30,25287 + 7,173061 (horas) – 0,1069887 ( ² horas)