Excel: como usar proj.lin para realizar regressão linear múltipla

Você pode usar a função PROJ.LIN no Excel para ajustar um modelo de regressão linear múltipla a um conjunto de dados.

Esta função usa a seguinte sintaxe básica:

 = LINEST ( known_y's, [known_x's], [const], [stats] )

Ouro:

• val_conhecidos_y : uma matriz de valores y conhecidos
• conhecidos_x’s : uma matriz de valores x conhecidos
• const : argumento opcional. Se TRUE, a constante b será processada normalmente. Se for FALSO, a constante b será definida como 1.
• estatísticas : argumento opcional. Se for TRUE, serão retornadas estatísticas de regressão adicionais. Se for FALSO, estatísticas de regressão adicionais não serão retornadas.

O exemplo passo a passo a seguir mostra como usar esta função na prática.

Passo 1: Insira os dados

Primeiro, vamos inserir o seguinte conjunto de dados no Excel:

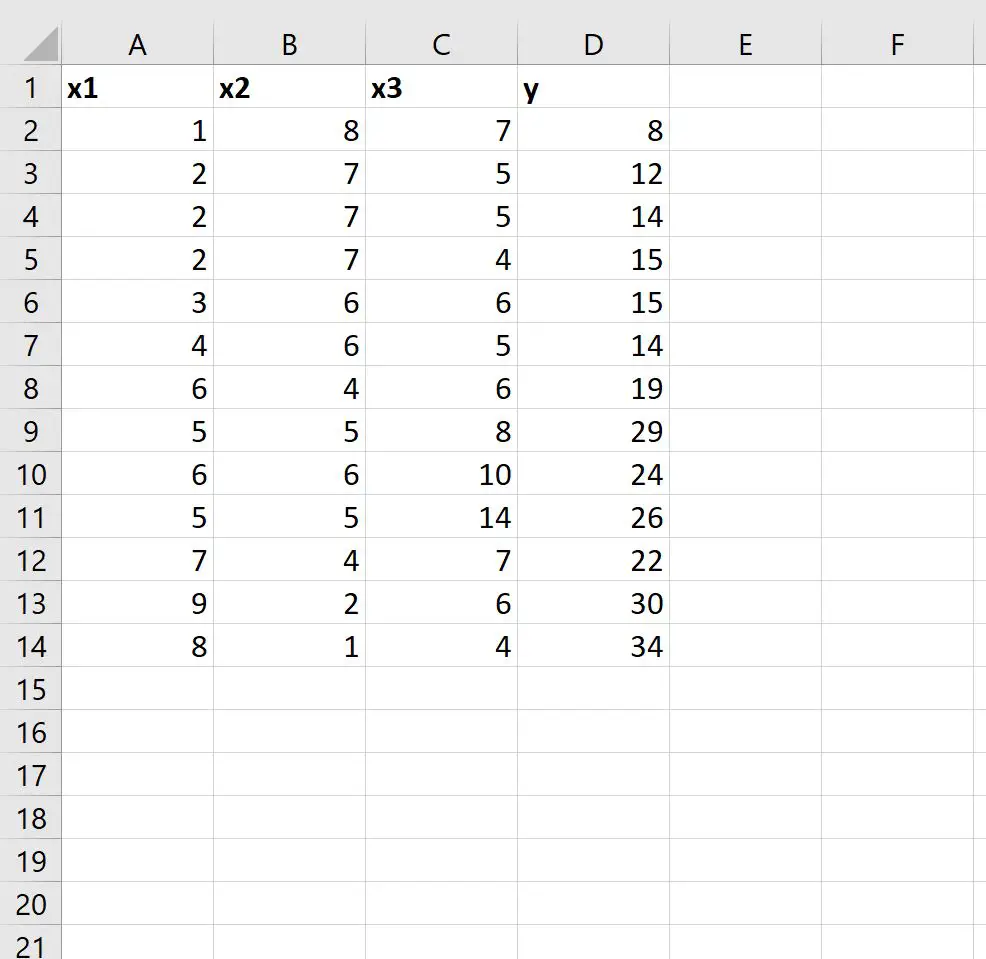
Etapa 2: usar PROJ.LIN para ajustar um modelo de regressão linear múltipla

Suponha que queiramos ajustar um modelo de regressão linear múltipla usando x1 , x2 e x3 como variáveis preditoras e y como variável de resposta.

Para fazer isso, podemos digitar a seguinte fórmula em qualquer célula para ajustar este modelo de regressão linear múltipla

 =LINEST( D2:D14 , A2:C14 )

A captura de tela a seguir mostra como usar esta fórmula na prática:

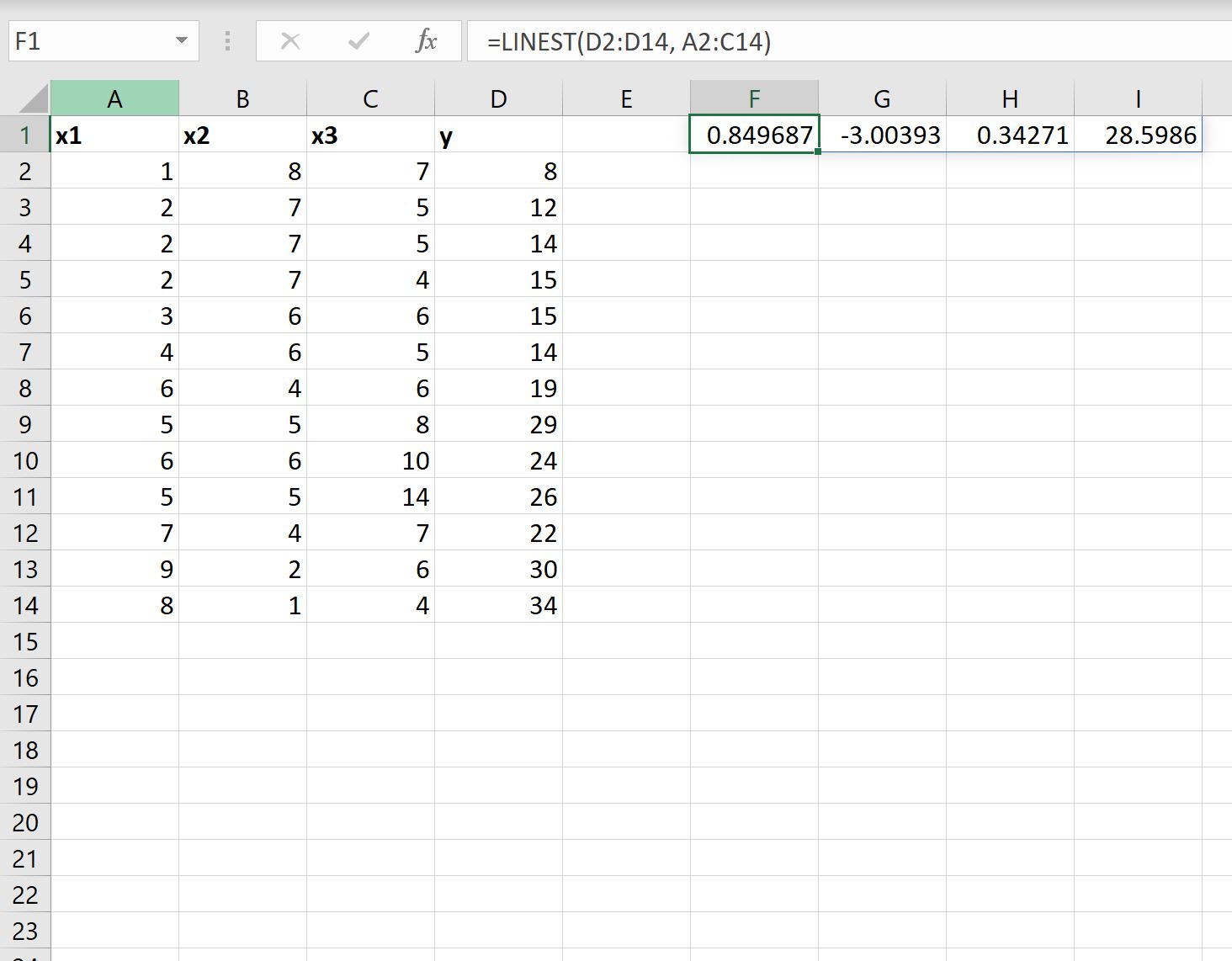
Veja como interpretar o resultado:

• O coeficiente da interceptação é 28,5986 .
• O coeficiente para x1 é 0,34271 .
• O coeficiente para x2 é -3,00393 .
• O coeficiente para x3 é 0,849687 .

Usando esses coeficientes, podemos escrever a equação de regressão ajustada da seguinte forma:

y = 28,5986 + 0,34271(x1) – 3,00393(x2) + 0,849687(x3)

Etapa 3 (opcional): visualizar estatísticas de regressão adicionais

Também podemos definir o valor do argumento stats na função PROJ.LIN igual a TRUE para exibir estatísticas de regressão adicionais para a equação de regressão ajustada:

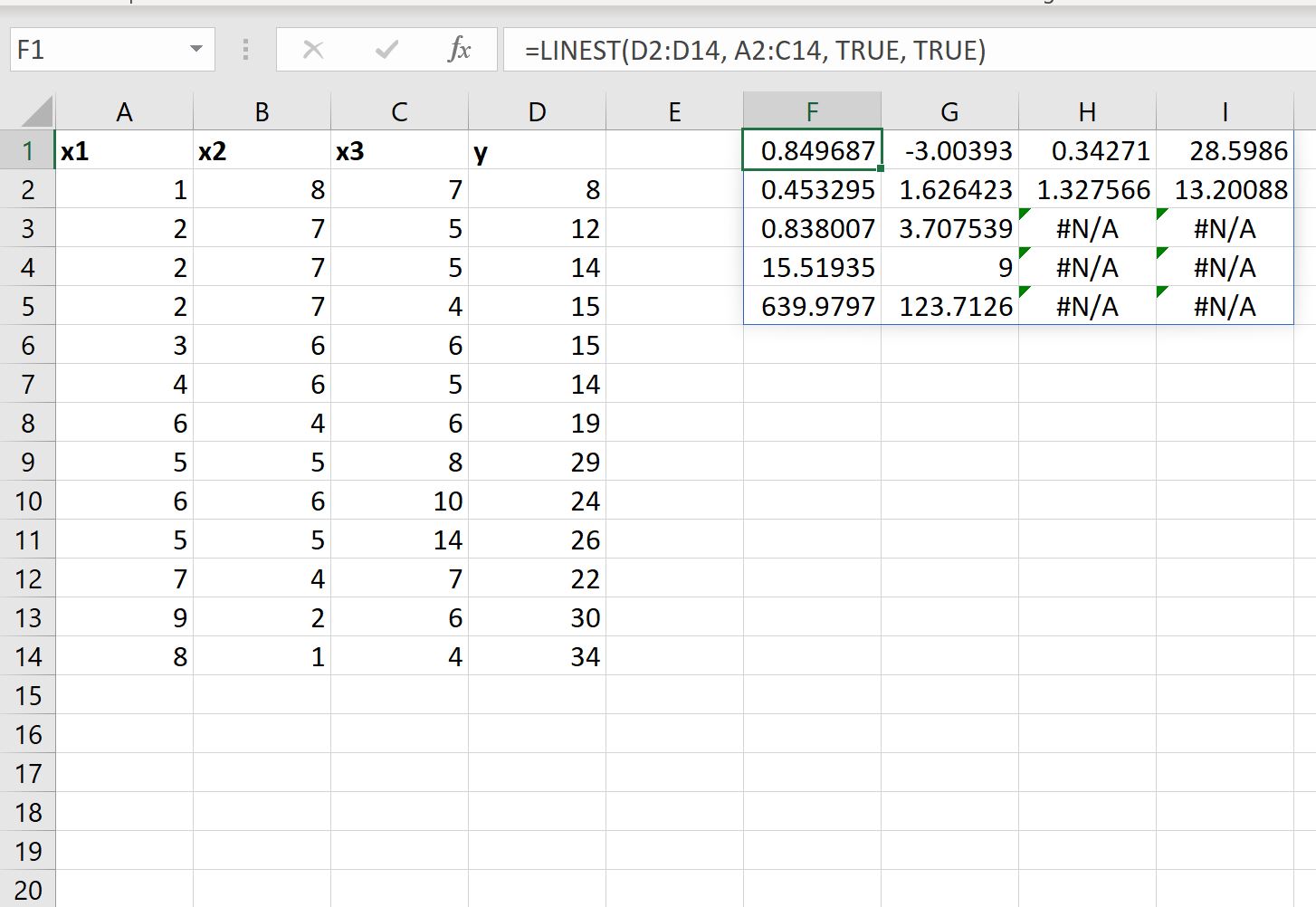
A equação de regressão ajustada ainda é a mesma:

y = 28,5986 + 0,34271(x1) – 3,00393(x2) + 0,849687(x3)

Veja como interpretar os outros valores do resultado:

• O erro padrão para x3 é 0,453295 .
• O erro padrão para x2 é 1,626423 .
• O erro padrão para x1 é 1.327566 .
• O erro padrão para a interceptação é 13.20088 .
• O R ² do modelo é 0,838007 .
• O erro padrão residual para y é 3,707539 .
• A estatística F geral é 15,51925 .
• Os graus de liberdade são 9 .
• A soma dos quadrados da regressão é 639,9797 .
• A soma residual dos quadrados é 123,7126 .

Em geral, a medida de maior interesse nestas estatísticas adicionais é o valor R ² , que representa a proporção da variância na variável resposta que pode ser explicada pela variável preditora.

O valor de R ² pode variar de 0 a 1.

Como o R ² deste modelo específico é 0,838 , isso nos diz que as variáveis preditoras estão fazendo um bom trabalho ao prever o valor da variável resposta y.

Relacionado: O que é um bom valor de R ao quadrado?

Recursos adicionais

Os tutoriais a seguir explicam como realizar outras operações comuns no Excel:

Como usar a função LOGEST no Excel
Como realizar regressão não linear no Excel
Como realizar regressão cúbica no Excel