Frequência acumulativa
Este artigo explica o que é frequência cumulativa nas estatísticas. Assim, você aprenderá o significado de frequência cumulativa, como a frequência cumulativa é calculada com exemplos e, por fim, os diferentes tipos de frequências cumulativas que existem.
O que é frequência cumulativa?
Nas estatísticas, a frequência cumulativa é a soma cumulativa das frequências. Ou seja, a frequência acumulada de um valor é igual à frequência desse valor mais as frequências de todos os valores inferiores.
Existem dois tipos de frequências cumulativas: frequência absoluta cumulativa e frequência relativa cumulativa. A seguir veremos como cada tipo de frequência cumulativa é calculada.
Tenha em mente que para entender o que significa frequência cumulativa nas estatísticas, primeiro você deve ter clareza sobre o conceito de frequência. É por isso que é recomendável visitar o seguinte post antes de continuar com a explicação:
Como calcular a frequência cumulativa
As etapas para calcular a frequência cumulativa de uma amostra estatística são:
- Crie uma tabela com todos os diferentes valores que aparecem no conjunto de dados, ordenados do menor para o maior.
- Encontre a frequência absoluta de cada valor.
- Encontre a frequência cumulativa de cada valor, que é calculada somando a frequência do próprio valor mais as frequências de todos os valores menores.
Portanto, a fórmula para cálculo da frequência acumulada é:
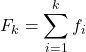
Ouro:
-
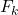
é a frequência cumulativa do valor

.
-

é a frequência absoluta do valor

.
Observe que essas etapas servem para calcular a frequência absoluta cumulativa, mas também existe a frequência relativa cumulativa. A seguir veremos a diferença entre esses dois tipos de frequências acumuladas e como cada tipo é encontrado.
Tipos de frequências cumulativas
Nas estatísticas, existem dois tipos de frequências cumulativas :
- Frequência absoluta acumulada : é a soma cumulativa das frequências absolutas .
- Frequência relativa cumulativa : é a soma cumulativa das frequências relativas .
Considerando a definição de cada tipo de frequência acumulada, você confere abaixo um exemplo de como cada uma é obtida.
Frequência absoluta acumulada
A frequência absoluta acumulada é representada pelo símbolo F i e é calculada somando as frequências absolutas de valores iguais ou inferiores ao valor em questão. A seguir, você tem um exemplo concreto em que a frequência absoluta cumulativa de um conjunto de dados estatísticos é calculada.
- As notas obtidas na disciplina de estatística numa turma de 30 alunos são as seguintes. Qual é a frequência absoluta acumulada de cada nota?
![]()
![]()
![]()
Como todos os números só podem ser inteiros, é uma variável discreta. Portanto, não é necessário agrupar os dados em intervalos.
Assim, para determinar a frequência absoluta acumulada, devemos primeiro encontrar a frequência absoluta de cada valor, que é o número de vezes que cada valor aparece na amostra estatística.

Agora que sabemos a frequência absoluta de cada valor, podemos calcular as suas frequências absolutas cumulativas. Para isso, temos duas opções: ou somamos a frequência absoluta do valor mais todas as frequências absolutas dos menores valores, ou pelo contrário, somamos a frequência absoluta do valor mais a frequência absoluta acumulada dos valores anteriores . valor.

Resumindo, a tabela com a frequência acumulada absoluta de exercício é a seguinte:

Observe que a frequência absoluta acumulada do último valor sempre coincide com o número total de dados. Caso contrário, significa que você cometeu um erro no cálculo.
Frequência relativa cumulativa
A frequência relativa acumulada é representada pelo símbolo H i e é calculada somando as frequências relativas de valores iguais ou inferiores ao valor em questão. Abaixo você pode ver um exercício resolvido com os mesmos dados do problema anterior no qual é determinada a frequência relativa cumulativa.
- As notas obtidas em estatística em uma turma de 30 alunos são as seguintes. Qual é a frequência relativa cumulativa de cada nota?
![]()
![]()
![]()
Neste caso, a variável é discreta, pois não pode assumir valor decimal. Portanto não há necessidade de agrupar os dados por intervalos, mas podemos fazer os cálculos diretamente.
Assim, elaboramos uma tabela de frequências e determinamos a frequência absoluta de cada valor diferente:

A seguir, calculamos a frequência relativa de cada valor, que é determinada dividindo a frequência absoluta pelo número total de observações (30).

E depois de calcularmos a frequência absoluta e a frequência relativa do conjunto de dados, podemos obter a frequência relativa cumulativa. Para isso, deve-se somar a frequência relativa do valor em questão mais todas as frequências relativas anteriores ou, o que dá no mesmo, a frequência relativa acumulada anterior:

Em suma, a tabela de frequência com frequência absoluta, frequência relativa e frequência relativa cumulativa é a seguinte:

Lembre-se de que o último valor da frequência relativa acumulada deve ser sempre 1. Se obtiver outro número, significa que cometeu um erro nos cálculos.