Frequência relativa cumulativa
Este artigo explica o que é frequência relativa cumulativa nas estatísticas. Assim, você encontrará a definição de frequência relativa cumulativa, como obter frequência relativa cumulativa e dois exercícios resolvidos passo a passo.
O que é frequência relativa cumulativa?
Nas estatísticas, a frequência relativa cumulativa é a soma cumulativa das frequências relativas. Ou seja, a frequência relativa cumulativa de um valor é igual à frequência relativa desse valor mais as frequências relativas de todos os valores menores que ele.
O símbolo para frequência relativa cumulativa é H i . No entanto, nas estatísticas ainda não existe um consenso completo quanto ao símbolo para este tipo de frequência, razão pela qual também poderá encontrá-lo expresso através de outro símbolo.
Obviamente, para entender o significado de frequência relativa cumulativa, você deve primeiro ter clareza sobre o conceito de frequência relativa, por isso recomendo que você visite o seguinte link antes de continuar com a explicação:
Como calcular a frequência relativa cumulativa
Para calcular a frequência relativa cumulativa, devem ser seguidos os seguintes passos:
- Construa uma tabela de frequências com todos os diferentes valores da amostra estatística.
- Calcule a frequência absoluta de cada valor.
- A partir das frequências absolutas, determine a frequência relativa de cada valor.
- Encontre a frequência relativa cumulativa de cada valor, que é calculada adicionando a frequência relativa do próprio valor mais as frequências relativas de todos os valores menores.
Lembre-se de que se você deseja calcular a porcentagem de frequência relativa acumulada , ou seja, a frequência relativa acumulada expressa em porcentagem, basta seguir os mesmos passos e multiplicar os resultados por 100.
Exemplos de frequência relativa cumulativa
Para que você possa ver como a frequência relativa acumulada é calculada, dois exemplos resolvidos passo a passo são mostrados a seguir. No primeiro exemplo encontramos a frequência relativa acumulada de uma variável discreta e no segundo exemplo uma variável contínua, pois o processo varia ligeiramente.
Exemplo 1: variável discreta
- As notas obtidas na disciplina de estatística numa turma de 30 alunos são as seguintes. Qual é a frequência relativa cumulativa de cada nota?
![]()
![]()
![]()
Neste caso, a variável é discreta, pois não pode assumir valor decimal. Portanto, não é necessário agrupar os dados por intervalos, mas os cálculos podem ser feitos diretamente.
Assim, elaboramos uma tabela de frequências e determinamos a frequência absoluta de cada valor diferente:

A seguir calculamos a frequência relativa de cada valor (você pode ver como isso é feito no link no início do post).

E depois de calcularmos a frequência absoluta e a frequência relativa do conjunto de dados, podemos obter a frequência relativa cumulativa. Para isso, devemos somar a frequência relativa do valor em questão mais todas as frequências relativas anteriores ou, em outras palavras, a frequência relativa acumulada anterior:

Em suma, a tabela de frequência com frequência absoluta, frequência relativa e frequência relativa cumulativa é a seguinte:

Lembre-se de que o último valor da frequência relativa acumulada deve ser sempre 1. Se obtiver outro número, significa que cometeu um erro nos cálculos.
Exemplo 2: variável contínua
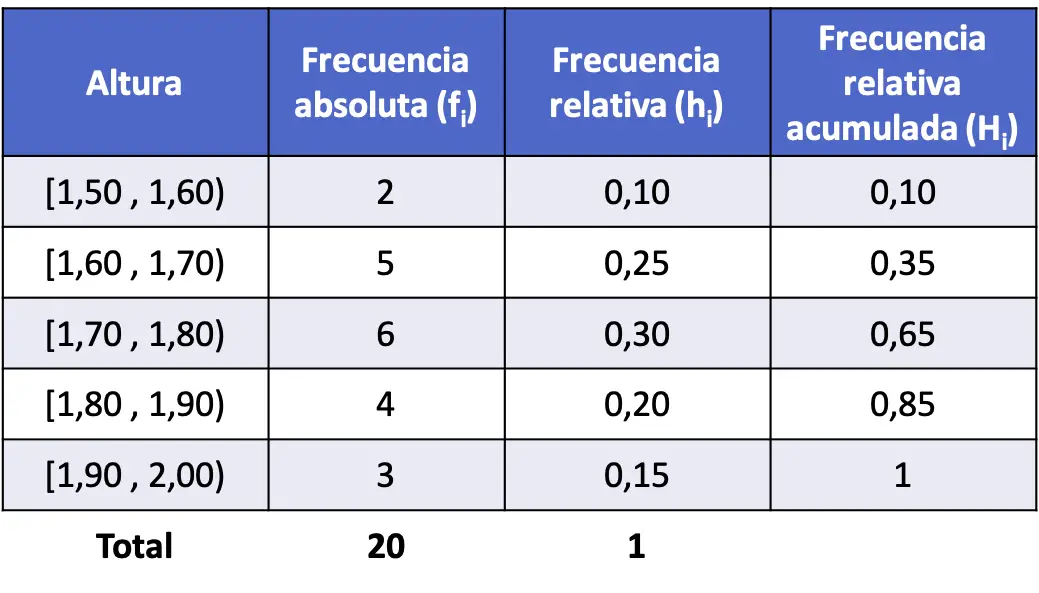
- A altura de 20 pessoas foi medida e os resultados abaixo foram obtidos. Separe os dados em intervalos e encontre a frequência relativa cumulativa de cada intervalo.
![]()
![]()
Este caso é diferente do problema anterior, pois os números são decimais, o que significa que a variável pode assumir qualquer valor e, portanto, é contínua. Portanto, criaremos a tabela de frequência agrupando os dados em intervalos.
Construímos, portanto, a tabela e obtemos a frequência absoluta de cada intervalo:

Agora calculamos as frequências relativas dividindo a frequência absoluta de cada intervalo pelo número total de pontos de dados:

E, finalmente, determinamos as frequências relativas cumulativas de todos os intervalos. Como antes, para determinar uma frequência relativa cumulativa de um intervalo é necessário adicionar a frequência relativa do referido intervalo mais as frequências relativas anteriores:
Frequência relativa cumulativa e frequência absoluta cumulativa
Acabamos de ver como a frequência relativa cumulativa é derivada da frequência relativa. Porém, esse tipo de frequência também pode ser encontrado usando a frequência absoluta acumulada.
A frequência relativa cumulativa pode ser calculada dividindo a frequência absoluta cumulativa pelo número total de dados na amostra.
Portanto, a fórmula para frequência relativa cumulativa é:
![]()
Ouro:
-
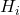
é a frequência relativa cumulativa.
-
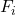
-

é o número total de dados.
Seguindo o primeiro exemplo desenvolvido acima, veja como a frequência relativa acumulada é encontrada a partir da frequência absoluta acumulada:
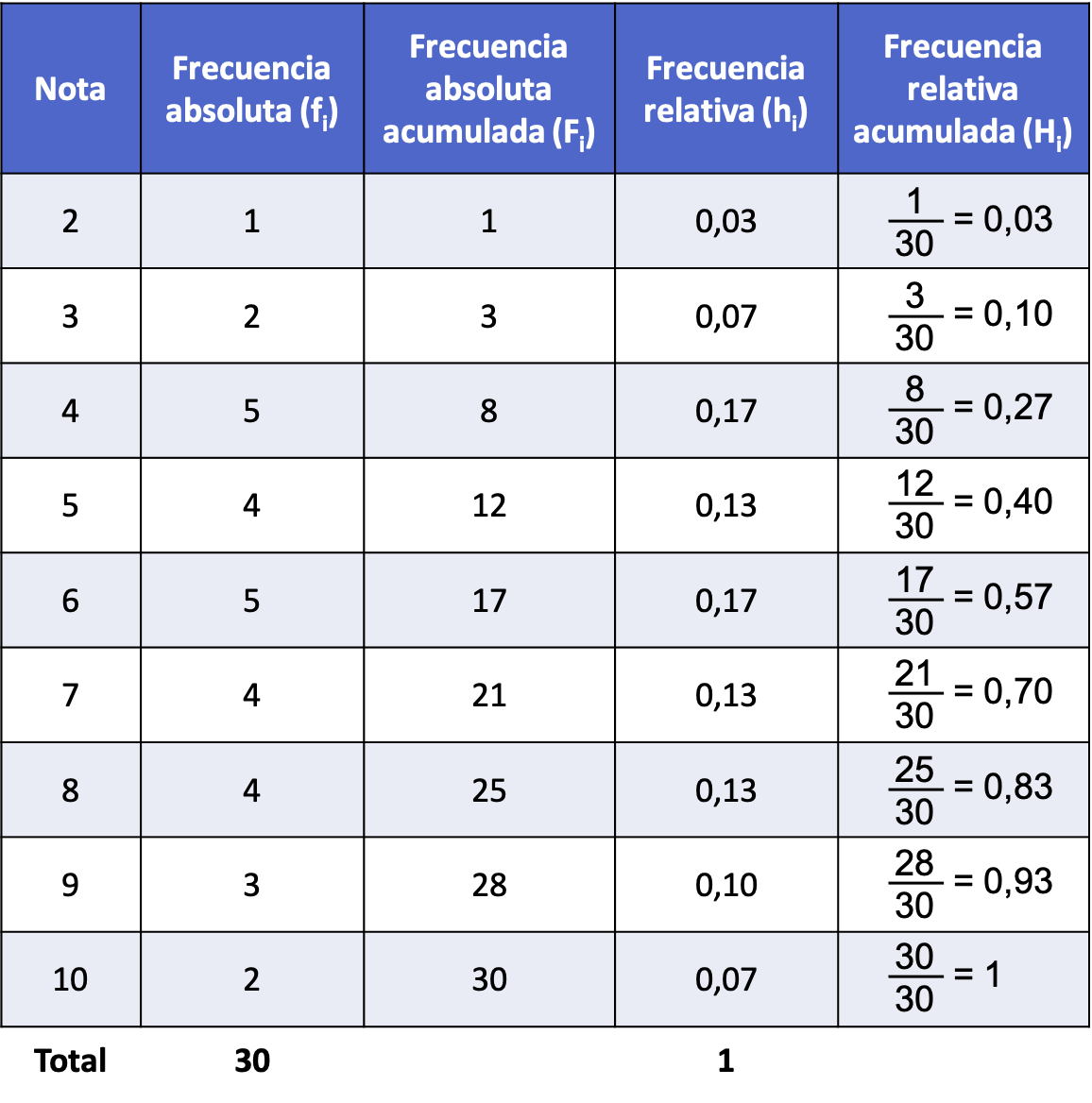
A tabela acima, por conter todos os tipos de frequências estatísticas, é chamada de tabela de frequências. Clique aqui para saber mais: