Função de densidade

By Dr. benjamim anderson Agosto 5, 2023 Probabilidade 0 Comments

Neste artigo você descobrirá o que é a função densidade, como uma probabilidade é calculada a partir da função densidade e as características desta função probabilística. Além disso, você poderá ver quais são as diferenças entre a função de densidade e a função de distribuição.

Qual é a função densidade?

A função densidade , também chamada de função densidade de probabilidade , é uma função matemática que descreve a probabilidade de uma variável aleatória contínua assumir um determinado valor.

Em outras palavras, a função densidade associada a uma variável define matematicamente as probabilidades de a variável assumir um valor.

Por exemplo, digamos que a probabilidade de uma pessoa adulta ter mais de 1,80 m de altura em uma população seja de 35%, então a função densidade indicará uma probabilidade de 35% no cálculo dessa probabilidade.

Às vezes, a função de densidade de probabilidade é abreviada como PDF.

Calcule uma probabilidade com a função de densidade

Para encontrar a probabilidade de uma variável contínua assumir um valor em um intervalo, é necessário calcular a integral da função densidade associada a essa variável entre os limites do intervalo.

$\displaystyle P[a\leq X\leq b]=\int_a^b f(x)dx$

Ouro

$f(x)$

é a função densidade da variável aleatória contínua.

Ou em outras palavras, a probabilidade de a variável assumir um valor em um intervalo é equivalente à área sob a função densidade nesse intervalo.

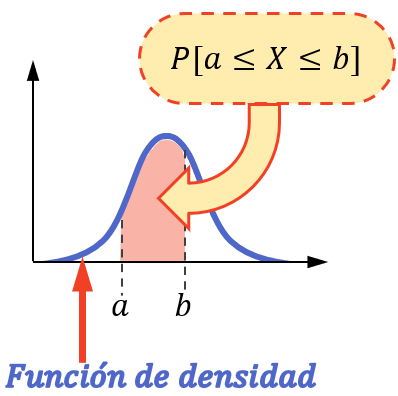
Observe que o cálculo de probabilidade só pode ser feito desta forma se a variável estatística seguir uma distribuição contínua, como distribuição normal, distribuição exponencial, distribuição de Poisson, etc.

Propriedades da função densidade

A função densidade tem as seguintes propriedades:

O valor da função densidade é zero ou positivo para qualquer valor de x.

$f(x)\geq 0$

Além disso, o valor máximo da função densidade é igual a 1.

$f(x)\leq 1$

Na verdade, a área total sob o gráfico da função densidade é sempre equivalente a 1 independentemente da variável, pois corresponde ao conjunto de todas as probabilidades.

$\displaystyle \int_{-\infty}^{+\infty} f(x)dx=1$

Conforme explicado na seção anterior, a probabilidade de uma variável contínua assumir um valor em um intervalo é calculada com a integral da função densidade nesse intervalo.

$\displaystyle P[a\leq X\leq b]=\int_a^b f(x)dx=F(b)-F(a)$

Função densidade e função distribuição

Nesta última seção, veremos como a função densidade e a função distribuição se diferenciam, pois são dois tipos de funções probabilísticas geralmente confundidas.

Matematicamente, a função de distribuição é equivalente à integral da função densidade , portanto a função de distribuição descreve a probabilidade cumulativa de uma variável contínua.

Ou seja, a imagem da função de distribuição para qualquer valor é igual à probabilidade de a variável assumir esse valor ou um valor inferior.

A relação matemática entre esses dois tipos de funções é, portanto, a seguinte:

$\displaystyle P[X\leq a]=\int_{-\infty}^a f(x)dx=F(a)$

Ouro

$f(x)$

é a função densidade e

$F(x)$

é a função de distribuição.

Observe como a representação gráfica da função densidade muda em relação à sua função de distribuição de uma variável que segue uma distribuição normal com média 1 e desvio padrão de 0,5:

diferença entre função de distribuição e função de densidade

Para saber mais sobre o recurso de distribuição, clique no link abaixo:

➤ Veja: função de distribuição

About Author

Dr. benjamim anderson

Olá, sou Benjamin, um professor aposentado de estatística que se tornou professor dedicado na Statorials. Com vasta experiência e conhecimento na área de estatística, estou empenhado em compartilhar meu conhecimento para capacitar os alunos por meio de Statorials. Saber mais