Função de distribuição
Neste artigo você encontrará a explicação da função de distribuição, como seus valores são calculados e um exemplo real da função de distribuição. Além disso, você poderá ver as diferenças entre uma função de distribuição e uma função de densidade.
Qual é a função de distribuição?
A função de distribuição , também chamada de função de distribuição cumulativa , é uma função matemática que indica a probabilidade cumulativa de uma distribuição. Ou seja, a imagem da função de distribuição para qualquer valor é igual à probabilidade de a variável assumir esse valor ou um valor inferior.
A função de distribuição cumulativa também pode ser referida pela sigla FDA, embora seu símbolo usual seja o F maiúsculo.
A função de distribuição é, portanto, definida pela seguinte fórmula:
![]()
Como calcular a função de distribuição
Explicamos então como calcular o valor da função de distribuição dependendo se a distribuição de probabilidade é discreta ou contínua.
Caixa discreta
Se a variável aleatória for discreta, a função de distribuição cumulativa é igual à soma das probabilidades de todos os valores iguais ou menores que x .
![]()
Ouro
![]()
é a função de probabilidade associada à variável discreta.
Caso continuado
Se a variável aleatória for contínua, a função de distribuição cumulativa é equivalente à integral da função densidade de menos infinito até o valor em questão.
![]()
Ouro
![]()
é a função de densidade associada à variável contínua.
Exemplo de função de distribuição
Agora que sabemos a definição de função de distribuição, vamos dar uma olhada em um exemplo prático passo a passo para aprender como calcular o valor de uma função de distribuição.
- Calcule a função de distribuição para o experimento aleatório de lançar uma moeda quatro vezes.
Para resolver o exercício, você deve primeiro calcular todas as probabilidades associadas ao número de caras obtidas durante os quatro lançamentos de moeda:

Assim, por se tratar de uma variável discreta, para determinar as imagens da função de distribuição basta somar as probabilidades até o valor da variável em questão:
![Rendered by QuickLaTeX.com \begin{array}{l}F(X\leq 0)=f(0)=0,0625\\[4ex]\begin{aligned}F(X\leq 1)& =f(0)+f(1)\\[1.1ex] & =0,0625+0,25=0,3125\end{aligned}\\[6ex]\begin{aligned}F(X\leq 2)& =f(0)+f(1)+f(2)\\[1.1ex] & =0,0625+0,25+0,375=0,6875\end{aligned}\\[6ex]\begin{aligned}F(X\leq 3)& =f(0)+f(1)+f(2)+f(3)\\[1.1ex] & =0,0625+0,25+0,375+0,25=0,9375\end{aligned}\\[6ex]\begin{aligned}F(X\leq 4)& =f(0)+f(1)+f(2)+f(3)+f(4)\\[1.1ex] & =0,0625+0,25+0,375+0,25+0,0625=1\end{aligned}\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-63c3574be5cdcf6de8b54f910c01e35e_l3.png)
Assim, os valores da função de distribuição do lançamento de cara no lançamento de quatro moedas independentes são os seguintes:
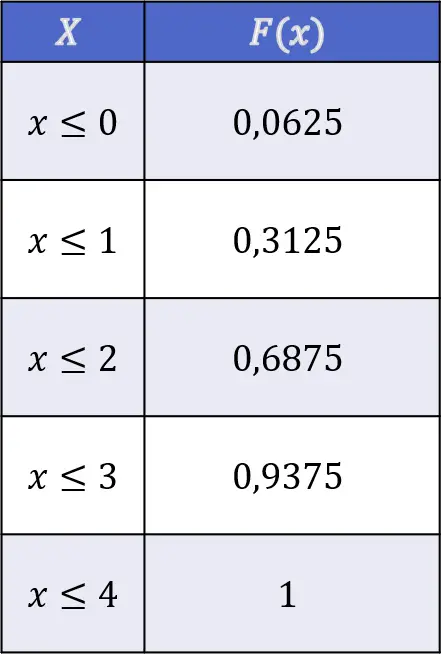
Propriedades da função de distribuição
Independentemente do tipo de variável, a função de distribuição sempre possui as seguintes propriedades:
- O valor da função de distribuição cumulativa está entre 0 e 1 inclusive.
![]()
- O limite de uma função de distribuição quando x tende ao infinito é igual a 1.
![]()
- Por outro lado, o limite de uma função de distribuição quando x se aproxima de menos infinito é zero.
![]()
- Pelas suas características, a função de distribuição é monotônica e não decrescente.
![]()
- Além disso, se
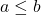
as seguintes equações são satisfeitas.
*** QuickLaTeX cannot compile formula:
\begin{array}{l}P(X < a) = F(a^-)\\[2ex] P(X>a)=1-F(a)\\[2ex]P(X \ge a )=1-F(a^-)\\[2ex]P(a<ul><li> Finally, if the statistical variable is continuous, the following equality is satisfied: </li></ul>[latex ]\begin{array}{l}P(a \le X < b) = \displaystyle\int_{a}^{b}f(x)\,dx = F(b)- F(a)\end{array}
*** Error message:
Missing $ inserted.
leading text: \begin{array}{l}
Please use \mathaccent for accents in math mode.
leading text: ... the statistical variable is continuous, the
Please use \mathaccent for accents in math mode.
leading text: ...iable statistic is continuous, equality
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \cr inserted.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
You can't use `\end' in internal vertical mode.
leading text: \end{document}
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}
Função de distribuição e função de densidade
Por fim, veremos qual é a diferença entre a função de distribuição e a função de densidade, uma vez que estas duas noções estatísticas são frequentemente confundidas.
A diferença entre a função de distribuição e a função de densidade é o tipo de probabilidade que elas definem. A função de densidade descreve a probabilidade de a variável assumir um determinado valor, enquanto a função de distribuição descreve a probabilidade cumulativa da variável.
Ou seja, a função de distribuição é utilizada para calcular a probabilidade de a variável ser igual ou menor que um determinado valor.
Observe que a função densidade se refere apenas a variáveis contínuas, portanto esta distinção só faz sentido se a variável em estudo for contínua.
Observe como a representação gráfica da função de distribuição muda em comparação com a função de densidade de uma variável que segue uma distribuição normal com média 1 e desvio padrão de 0,5:

Para saber mais sobre a função densidade, consulte o seguinte artigo: