Função de probabilidade

Este artigo explica o que são funções de probabilidade. Assim, você encontrará o significado de uma função de probabilidade, suas propriedades e um exemplo concreto de cálculo de uma função de probabilidade. Adicionalmente, são apresentadas as diferenças entre uma função de probabilidade e outros tipos de funções probabilísticas.

O que é uma função de probabilidade?

Uma função de probabilidade , também chamada de função de massa de probabilidade , é uma função matemática que descreve a probabilidade de uma variável aleatória discreta assumir um determinado valor.

Ou seja, uma função de probabilidade retorna a probabilidade associada a uma variável discreta de ser exatamente igual a um valor.

Por exemplo, a probabilidade de lançar qualquer número ao lançar um dado é 1/6 (um dado tem seis lados), portanto, a função de probabilidade associada a este espaço amostral será igual a 1/6 para n, não importa o valor.

Propriedades da função de probabilidade

As funções de probabilidade têm as seguintes propriedades:

• As probabilidades não podem ser negativas, então a função de probabilidade é zero ou positiva para qualquer valor de x.

• Da mesma forma, a probabilidade máxima é a unidade, o que significa que o evento sempre ocorrerá. Portanto, o valor máximo da função de probabilidade é igual a 1.

• Por fim, a soma de todos os valores de uma função de probabilidade dá 1, pois é a soma de todas as probabilidades no espaço amostral.

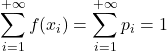
Exemplo de função de probabilidade

Agora que conhecemos a definição e as características da função de probabilidade, vejamos um exemplo deste tipo de função probabilística.

• Calcule as probabilidades de obter cara 0, 1, 2, 3 e 4 vezes fazendo quatro lançamentos de moeda independentes. A seguir, faça um gráfico da função de probabilidade encontrada.

Primeiramente devemos calcular as probabilidades de obter cara, para isso devemos dividir os casos possíveis pelo número total de casos. Você pode ver o cálculo de todas as probabilidades na tabela a seguir:

E uma vez calculadas todas as probabilidades, podemos representar os valores da função de probabilidade em um gráfico:

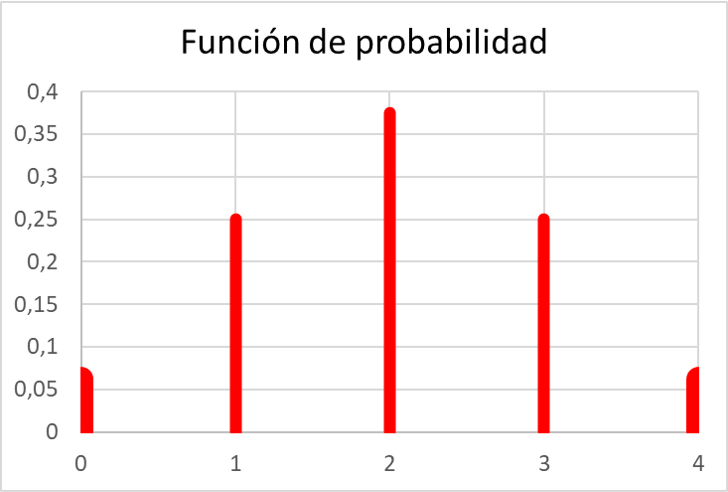
Como você pode ver, a função probabilística do exercício atende todas as propriedades das funções de probabilidade, pois todos os seus valores estão entre 0 e 1 e, além disso, a soma de todos os seus valores equivale a 1.

Função de probabilidade e função de densidade

Nesta seção veremos a diferença entre função de probabilidade e função de densidade, pois são dois tipos de funções probabilísticas que têm a mesma finalidade, mas são utilizadas em casos diferentes.

A diferença entre a função de probabilidade e a função de densidade é o tipo de variável para a qual as probabilidades descrevem. A função de probabilidade é usada para definir as probabilidades de uma variável discreta, enquanto a função de densidade é usada para definir as probabilidades de uma variável contínua.

Assim, dependendo da variável, é utilizada uma função de probabilidade ou uma função de densidade.

Para saber mais sobre a função densidade, clique no link a seguir:

Função de probabilidade e função de distribuição

A diferença entre uma função de probabilidade e uma função de distribuição é o tipo de probabilidade que elas definem. A função de probabilidade indica a probabilidade de a variável assumir um determinado valor, enquanto a função de distribuição descreve a probabilidade cumulativa da variável.

Portanto, a função de distribuição é calculada a partir da função de probabilidade.

Como exemplo, no link a seguir você pode ver o cálculo da função de distribuição para obter cara em quatro lançamentos de moeda, com base na função de probabilidade encontrada no exercício acima.