Como gerar uma distribuição normal em r (com exemplos)

Você pode gerar rapidamente uma distribuição normal em R usando a função rnorm() , que usa a seguinte sintaxe:

 rnorm(n, mean=0, sd=1)

Ouro:

• n: Número de observações.
• média: média da distribuição normal. O valor padrão é 0.
• dp: desvio padrão da distribuição normal. O valor padrão é 1.

Este tutorial mostra um exemplo de uso desta função para gerar uma distribuição normal em R.

Relacionado: Um guia para dnorm, pnorm, qnorm e rnorm em R

Exemplo: gerando uma distribuição normal em R

O código a seguir mostra como gerar uma distribuição normal em R:

 #make this example reproducible
set.seed(1)

#generate sample of 200 obs. that follows normal dist. with mean=10 and sd=3
data <- rnorm(200, mean=10, sd=3)

#view first 6 observations in sample
head(data)

[1] 8.120639 10.550930 7.493114 14.785842 10.988523 7.538595

Podemos encontrar rapidamente a média e o desvio padrão desta distribuição:

 #find mean of sample
mean(data)

[1] 10.10662

#find standard deviation of sample
sd(data)

[1] 2.787292

Também podemos criar um histograma rápido para visualizar a distribuição dos valores dos dados:

 hist(data, col=' steelblue ')

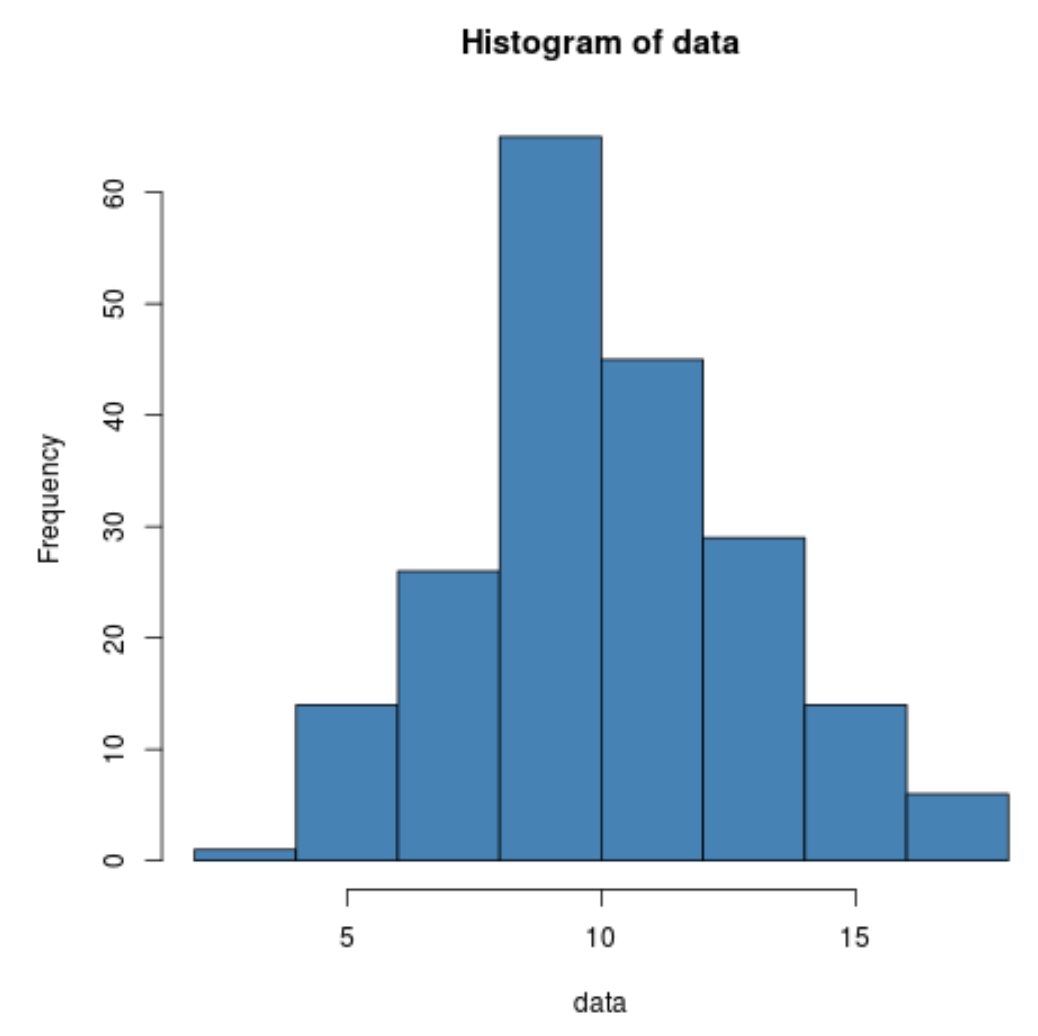
Podemos até realizar umteste de Shapiro-Wilk para ver se o conjunto de dados vem de uma população normal:

 shapiro.test(data)

	Shapiro-Wilk normality test

data:data
W = 0.99274, p-value = 0.4272

O valor p do teste acabou sendo 0,4272 . Como este valor não é inferior a 0,05, podemos assumir que os dados amostrais provêm de uma população normalmente distribuída.

Este resultado não deve ser surpreendente, uma vez que geramos os dados usando a função rnorm() , que gera naturalmente uma amostra aleatória de dados de uma distribuição normal.

Recursos adicionais

Como traçar uma distribuição normal em R
Um guia para dnorm, pnorm, qnorm e rnorm em R
Como realizar um teste de Shapiro-Wilk para normalidade em R