Como traçar uma distribuição de poisson em r

Para traçar a função de massa de probabilidade para uma distribuição de Poisson em R, podemos usar as seguintes funções:

• dpois(x, lambda) para criar a função de massa de probabilidade
• plot(x, y, type = ‘h’) para traçar a função de massa de probabilidade, especificando que o gráfico é um histograma (type=’h’)

Para traçar a função de massa de probabilidade, basta especificar lambda   (por exemplo, a taxa de ocorrência de eventos) na função dpois() .

Por exemplo, o código a seguir ilustra como traçar uma função de massa de probabilidade para uma distribuição de Poisson com lambda = 5:

 #define range of "successes"
success <- 0:20

#create plot of probability mass function
plot(success, dois(success, lambda=5), type='h')

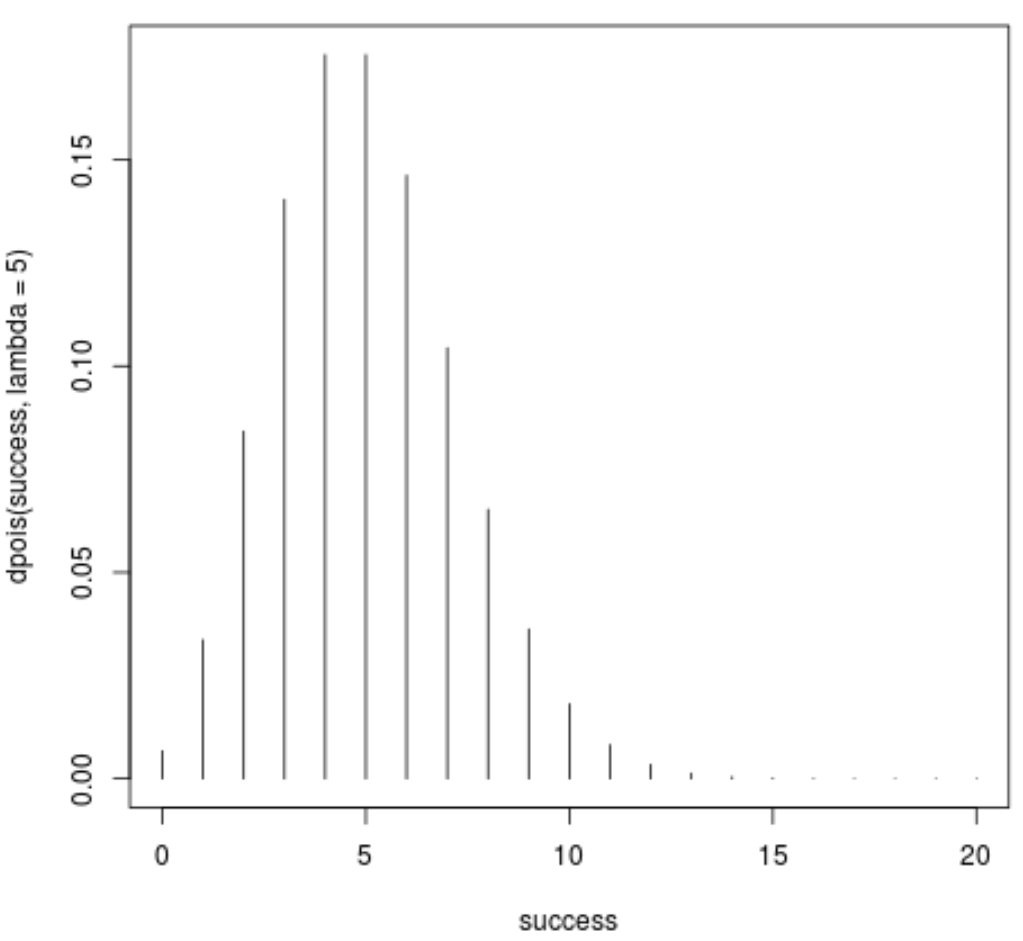
O eixo x mostra o número de “sucessos” – por exemplo, o número de eventos que ocorreram – e o eixo y mostra a probabilidade de alcançar esse número de sucessos em 20 tentativas.

Podemos adicionar um título, alterar os rótulos dos eixos e aumentar a largura das linhas para tornar o gráfico mais esteticamente agradável:

 success <- 0:20

plot(success, dois(success, lambda=5),
     type='h',
     main='Fish Distribution (lambda = 5)',
     ylab='Probability',
     xlab ='# Successes',
     lwd=3)

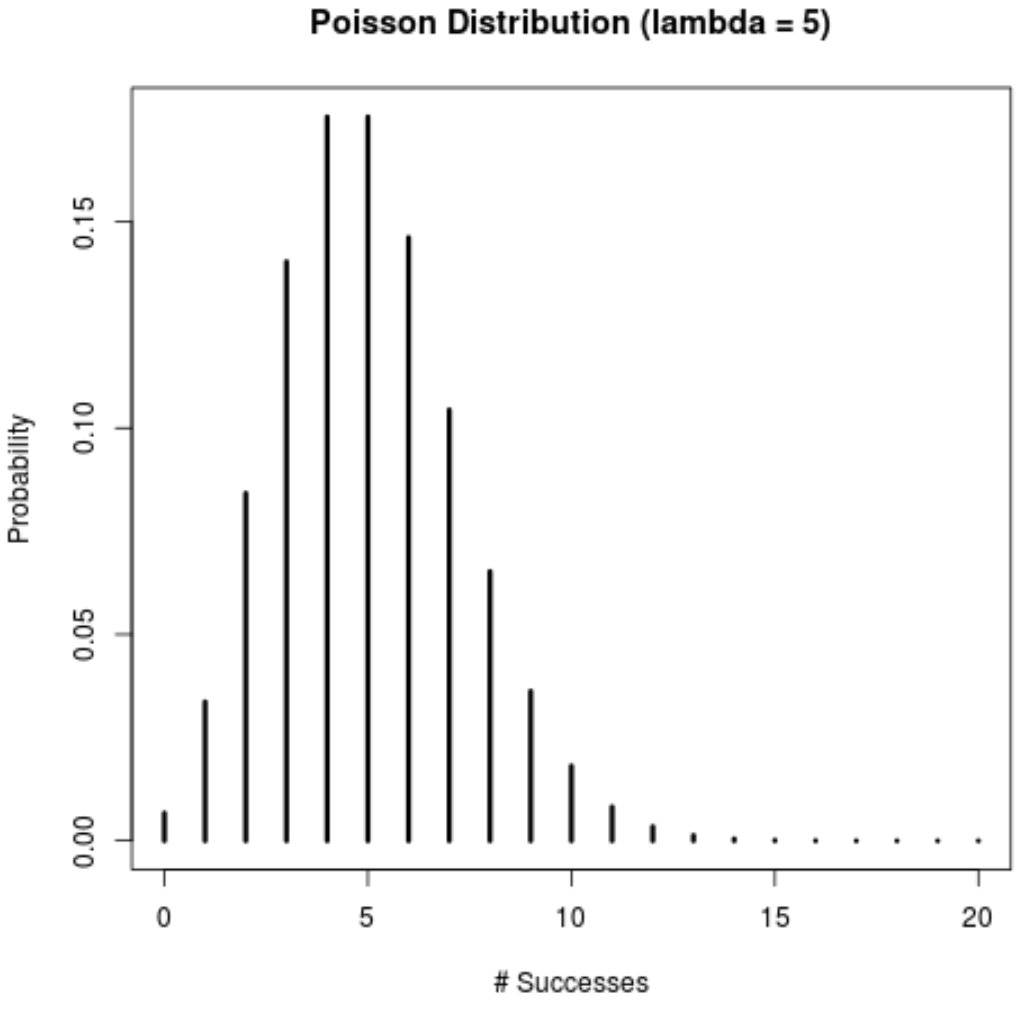
Podemos usar o código a seguir para obter as probabilidades reais para cada número de sucessos exibido no gráfico:

 #prevent R from displaying numbers in scientific notation
options(scipen=999) 

#define range of successes
success <- 0:20

#display probability of success for each number of trials
dpois(success, lambda=5)

[1] 0.0067379469991 0.0336897349954 0.0842243374886 0.1403738958143
[5] 0.1754673697679 0.1754673697679 0.1462228081399 0.1044448629571
[9] 0.0652780393482 0.0362655774156 0.0181327887078 0.0082421766854
[13] 0.0034342402856 0.0013208616483 0.0004717363030 0.0001572454343
[17] 0.0000491391982 0.0000144527054 0.0000040146404 0.0000010564843
[21] 0.0000002641211