Como criar um caminho residual manualmente

Um gráfico residual é um tipo de gráfico que exibe os valores de uma variável preditora em um modelo de regressão ao longo do eixo x e os valores dos resíduos ao longo do eixo y.

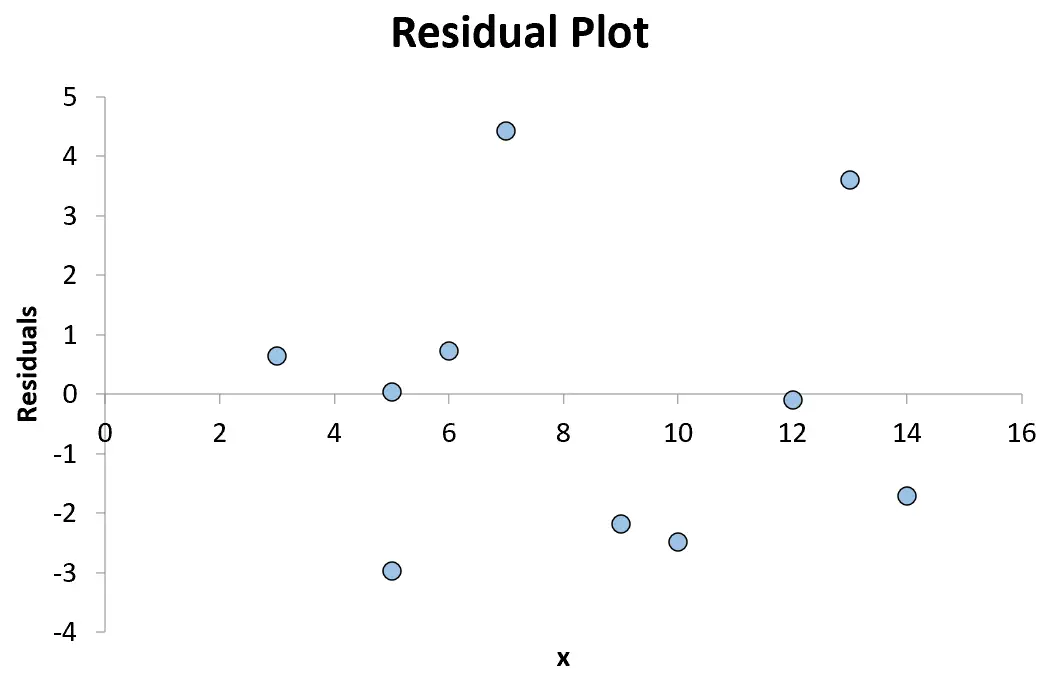
Este gráfico é utilizado para avaliar se os resíduos de um modelo de regressão são normalmente distribuídos e se apresentam ou não heterocedasticidade .

O exemplo passo a passo a seguir mostra como criar manualmente um gráfico residual para um modelo de regressão.

Etapa 1: Encontre os valores previstos

Suponha que queiramos ajustar um modelo de regressão ao seguinte conjunto de dados:

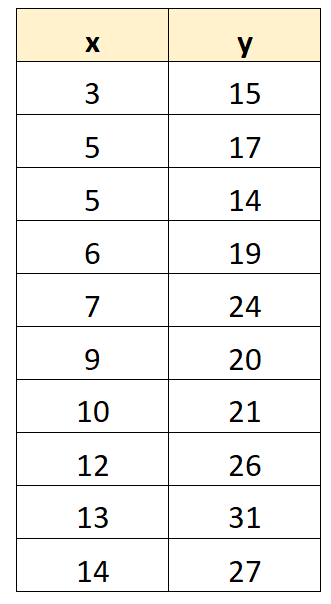
Usando software estatístico (como Excel, R, Python, SPSS, etc.), podemos ver que o modelo de regressão ajustado é:

y = 10,4486 + 1,3037(x)

Podemos então usar este modelo para prever o valor de y, com base no valor de x. Por exemplo, se x = 3, então prevemos que y será:

y = 10,4486 + 1,3037(3) = 14,359

Podemos repetir esse processo para cada observação em nosso conjunto de dados:

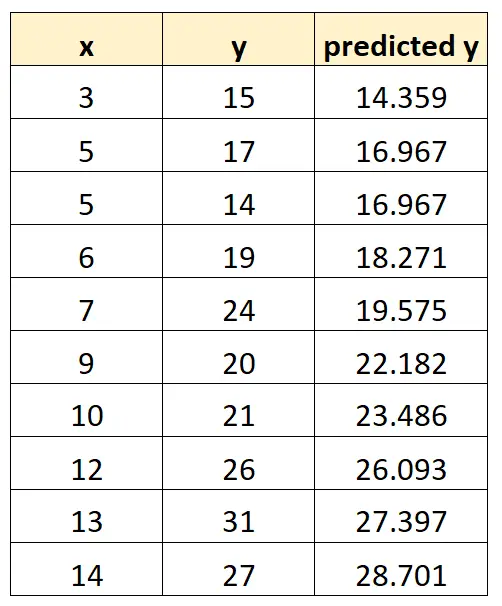
Etapa 2: Encontre os resíduos

Um resíduo para uma determinada observação em nosso conjunto de dados é calculado da seguinte forma:

Residual = valor observado – valor previsto

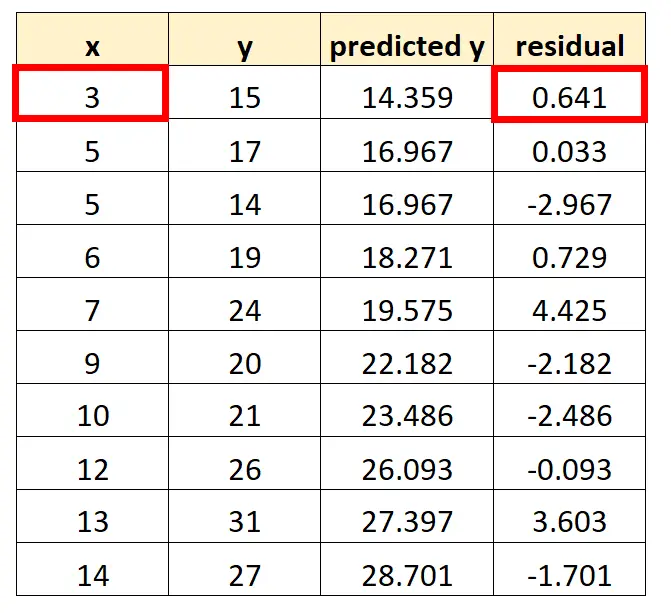
Por exemplo, o resíduo da primeira observação seria calculado da seguinte forma:

Residual = 15 – 14,359 = 0,641

Podemos repetir esse processo para cada observação em nosso conjunto de dados:

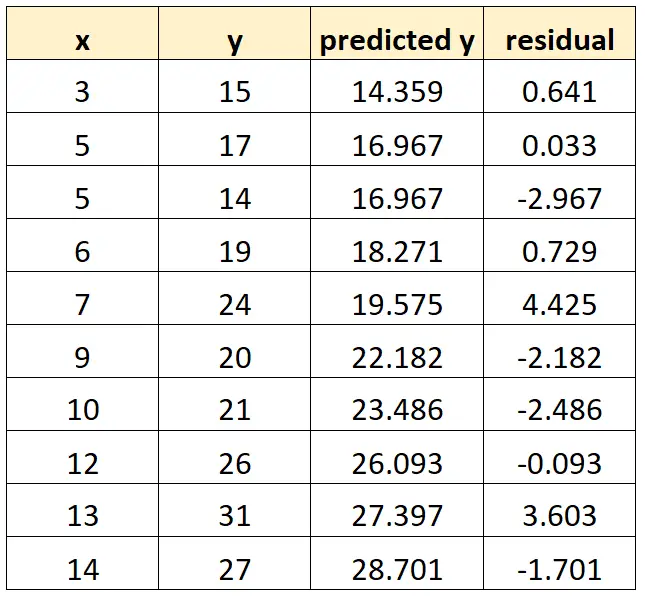
Passo 3: Crie o gráfico residual

Finalmente, podemos criar um gráfico de resíduos colocando os valores de x ao longo do eixo x e os resíduos ao longo do eixo y.

Por exemplo, o primeiro ponto que colocaremos em nosso gráfico é (3, 0,641)

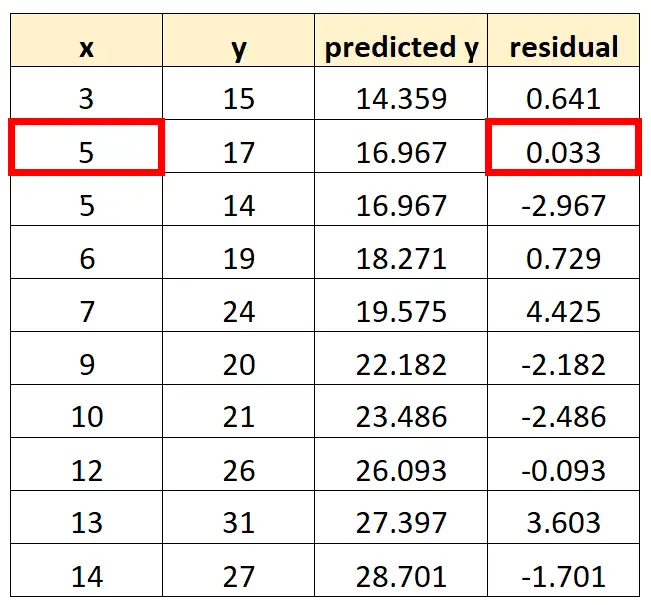
O próximo ponto que colocaremos em nosso gráfico é (5, 0,033)

Continuaremos até colocarmos todas as 10 combinações de pares de valores x e resíduos no gráfico:

Qualquer ponto acima de zero no gráfico representa um resíduo positivo. Isto significa que o valor observado para y é maior que o valor previsto pelo modelo de regressão.

Qualquer ponto menor que zero representa um resíduo negativo. Isto significa que o valor observado para y é inferior ao valor previsto pelo modelo de regressão.

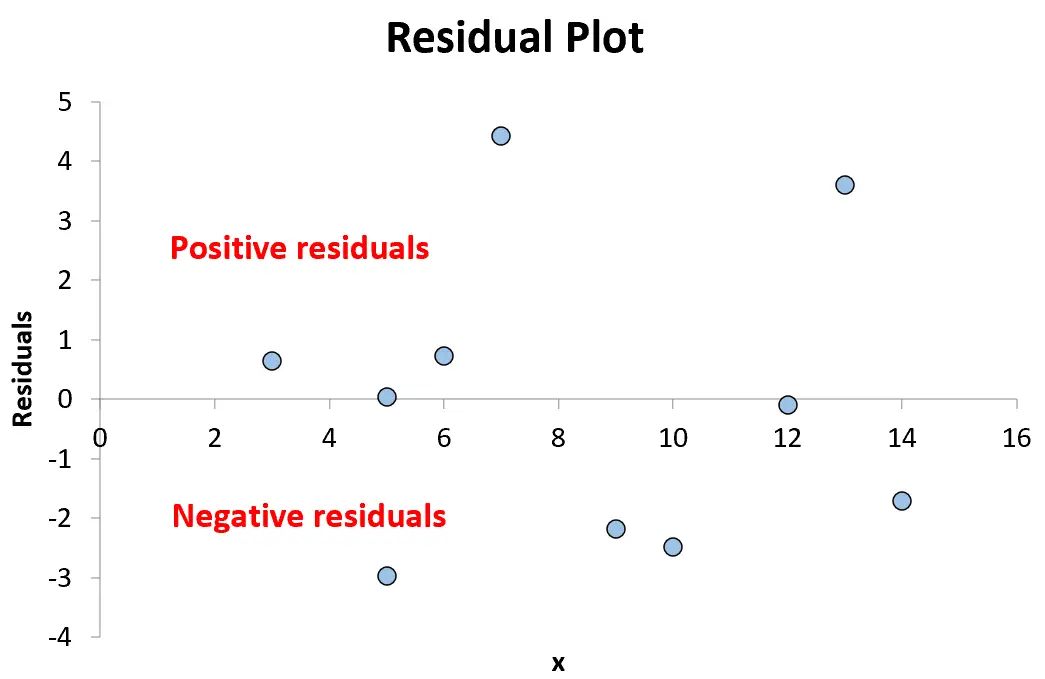
Como os pontos no gráfico estão espalhados aleatoriamente em torno de um resíduo de 0 sem um padrão claro, isso indica que a relação entre x e y é linear e é apropriado usar um modelo de regressão linear.

E como os resíduos não aumentam ou diminuem sistematicamente à medida que a variável preditora aumenta, isso significa que a heterocedasticidade não é um problema com este modelo de regressão.

Recursos adicionais

Os tutoriais a seguir explicam como criar gráficos residuais usando diferentes softwares estatísticos:

Como criar um gráfico residual em uma calculadora TI-84
Como criar um gráfico residual no Excel
Como criar um gráfico residual em R
Como criar um gráfico residual em Python