Como criar gráficos de resíduos parciais em r
A regressão linear múltipla é um método estatístico que podemos usar para compreender a relação entre múltiplas variáveis preditoras e uma variável de resposta .
No entanto, uma das principais suposições da regressão linear múltipla é que existe uma relação linear entre cada variável preditora e a variável de resposta.
Se esta suposição não for satisfeita, os resultados do modelo de regressão poderão não ser fiáveis.
Uma maneira de testar essa suposição é criar um gráfico de resíduos parciais , que exibe os resíduos de uma variável preditora em relação à variável de resposta.
O exemplo a seguir mostra como criar gráficos de resíduos parciais para um modelo de regressão em R.
Exemplo: Como criar gráficos de resíduos parciais em R
Suponha que ajustamos um modelo de regressão com três variáveis preditoras em R:
#make this example reproducible set. seeds (0) #define response variable y <- c(1:1000) #define three predictor variables x1 <- c(1:1000)*runif(n=1000) x2 <- (c(1:1000)*rnorm(n=1000))^2 x3 <- (c(1:1000)*rnorm(n=1000))^3 #fit multiple linear regression model model <- lm(y~x1+x2+x3))
Podemos usar a função crPlots() do pacote car em R para criar gráficos residuais parciais para cada variável preditora no modelo:
library (car) #create partial residual plots crPlots(model)
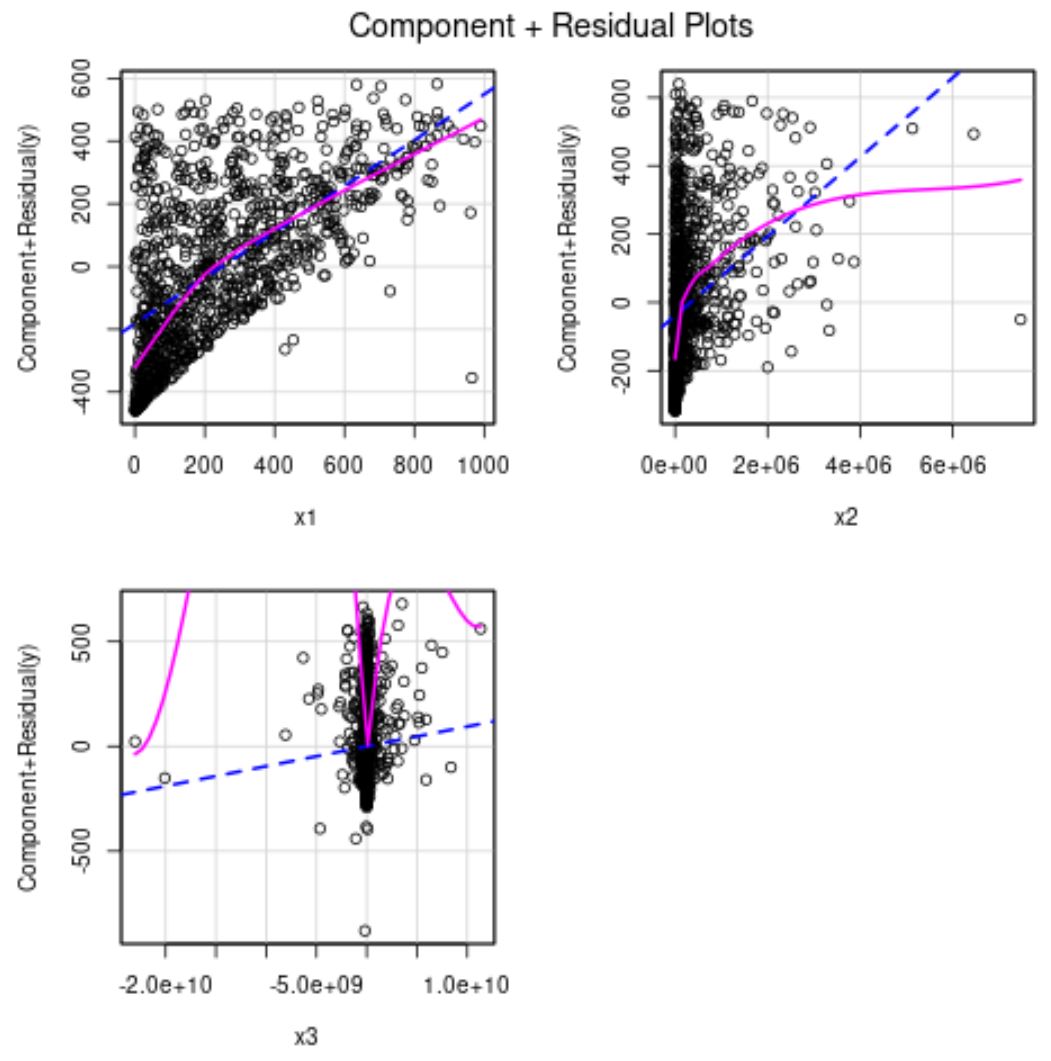
A linha azul mostra os resíduos esperados se a relação entre o preditor e a variável resposta fosse linear. A linha rosa mostra os resíduos reais.
Se as duas linhas forem significativamente diferentes, isso indica uma relação não linear.
Nos gráficos acima podemos ver que os resíduos para x2 e x3 parecem não lineares.
Isso viola a suposição de linearidade da regressão linear múltipla. Uma maneira de resolver esse problema é usar uma transformação de raiz quadrada ou cúbica nas variáveis preditoras:
library (car) #fit new model with transformed predictor variables model_transformed <- lm(y~x1+sqrt(x2)+log10(x3^(1/3))) #create partial residual plots for new model crPlots(model_transformed)
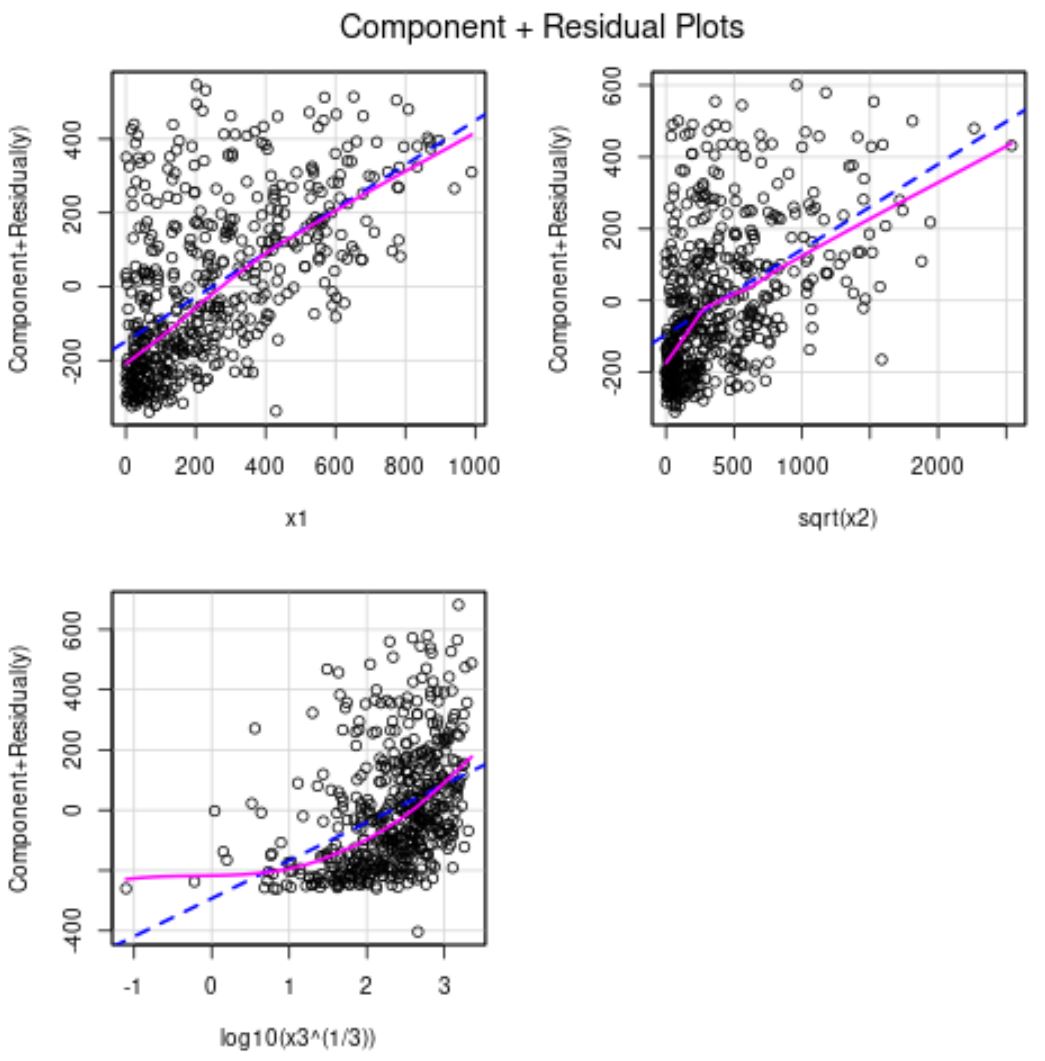
A partir dos gráficos de resíduos parciais, podemos ver que x2 agora tem uma relação mais linear com a variável resposta.
A variável preditora x3 ainda é um tanto não linear, então podemos decidir tentar outra transformação ou possivelmente remover completamente a variável do modelo.
Recursos adicionais
Os tutoriais a seguir explicam como criar outros gráficos comuns em R:
Como criar gráficos de diagnóstico em R
Como criar um gráfico de escala e localização em R
Como criar um gráfico residual em R