Como criar um gráfico residual em python

Um gráfico residual é um tipo de gráfico que exibe valores ajustados em relação aos resíduos de um modelo de regressão .

Este tipo de gráfico é frequentemente usado para avaliar se um modelo de regressão linear é ou não apropriado para um determinado conjunto de dados e para verificar a heterocedasticidade dos resíduos.

Este tutorial explica como criar um gráfico residual para um modelo de regressão linear em Python.

Exemplo: gráfico residual em Python

Para este exemplo, usaremos um conjunto de dados que descreve os atributos de 10 jogadores de basquete:

 import numpy as np
import pandas as pd

#create dataset
df = pd.DataFrame({'rating': [90, 85, 82, 88, 94, 90, 76, 75, 87, 86],
                   'points': [25, 20, 14, 16, 27, 20, 12, 15, 14, 19],
                   'assists': [5, 7, 7, 8, 5, 7, 6, 9, 9, 5],
                   'rebounds': [11, 8, 10, 6, 6, 9, 6, 10, 10, 7]})

#view dataset
df

	rating points assists rebounds
0 90 25 5 11
1 85 20 7 8
2 82 14 7 10
3 88 16 8 6
4 94 27 5 6
5 90 20 7 9
6 76 12 6 6
7 75 15 9 10
8 87 14 9 10
9 86 19 5 7

Gráfico residual para regressão linear simples

Suponha que ajustamos um modelo de regressão linear simples usando pontos como variável preditora e nota como variável resposta:

 #import necessary libraries
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.formula.api import ols

#fit simple linear regression model
model = ols('rating ~ points', data=df). fit ()

#view model summary
print(model.summary())

Podemos criar um gráfico residual ou ajustado usando a função plot_regress_exog() da biblioteca statsmodels:

 #define figure size
fig = plt.figure(figsize=(12,8))

#produce regression plots
fig = sm.graphics.plot_regress_exog(model, ' points ', fig=fig)

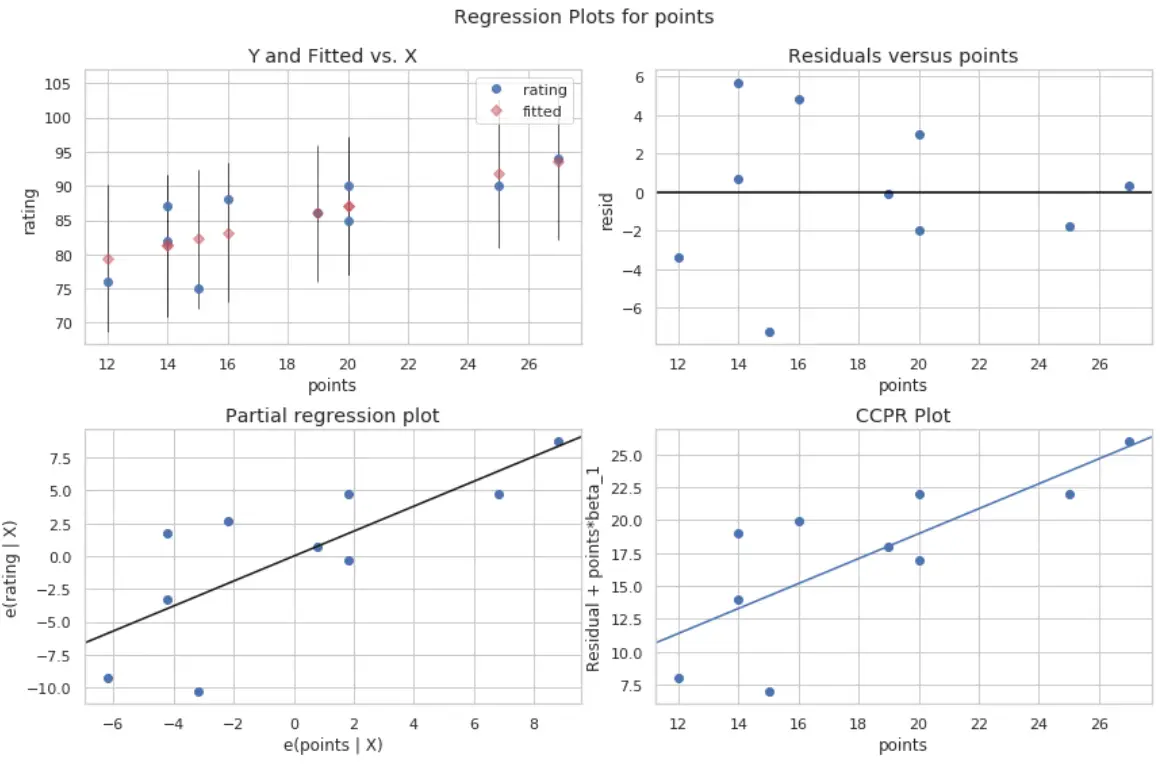
Quatro parcelas são produzidas. O que está no canto superior direito é o gráfico residual versus o gráfico ajustado. O eixo x neste gráfico mostra os valores reais dos pontos da variável preditora e o eixo y mostra o resíduo para esse valor.

Como os resíduos parecem estar espalhados aleatoriamente em torno de zero, isso indica que a heterocedasticidade não é um problema com a variável preditora.

Gráficos residuais para regressão linear múltipla

Suponha que, em vez disso, ajustemos um modelo de regressão linear múltipla usando assistências e rebotes como variável preditora e classificação como variável de resposta:

 #fit multiple linear regression model
model = ols('rating ~ assists + rebounds', data=df). fit ()

#view model summary
print(model.summary())

Mais uma vez, podemos criar um gráfico residual versus preditor para cada um dos preditores individuais usando a função plot_regress_exog() da biblioteca statsmodels.

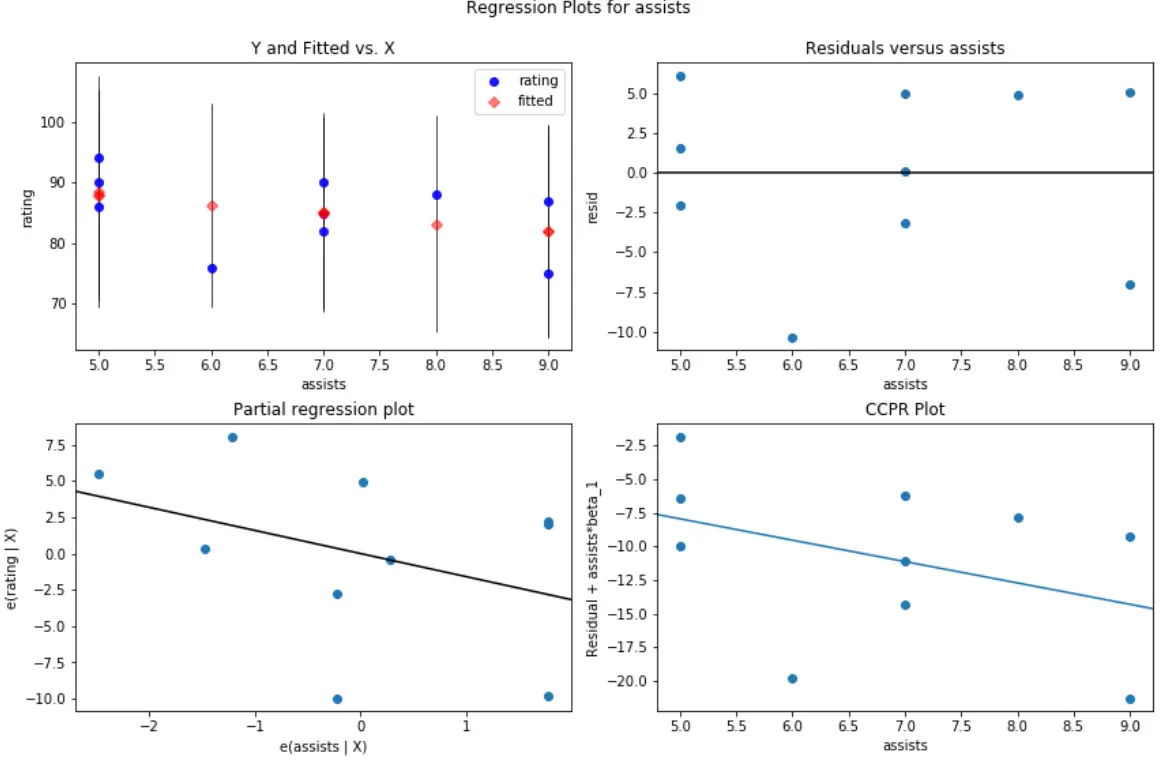
Por exemplo, esta é a aparência do gráfico residual/preditor para assistências de variáveis preditoras:

 #create residual vs. predictor plot for 'assists'
fig = plt.figure(figsize=(12,8))
fig = sm.graphics.plot_regress_exog(model, ' assists ', fig=fig)

E é assim que o gráfico residual/preditor se parece para os saltos da variável preditora:

 #create residual vs. predictor plot for 'assists'
fig = plt.figure(figsize=(12,8))
fig = sm.graphics.plot_regress_exog(model, ' rebounds ', fig=fig)

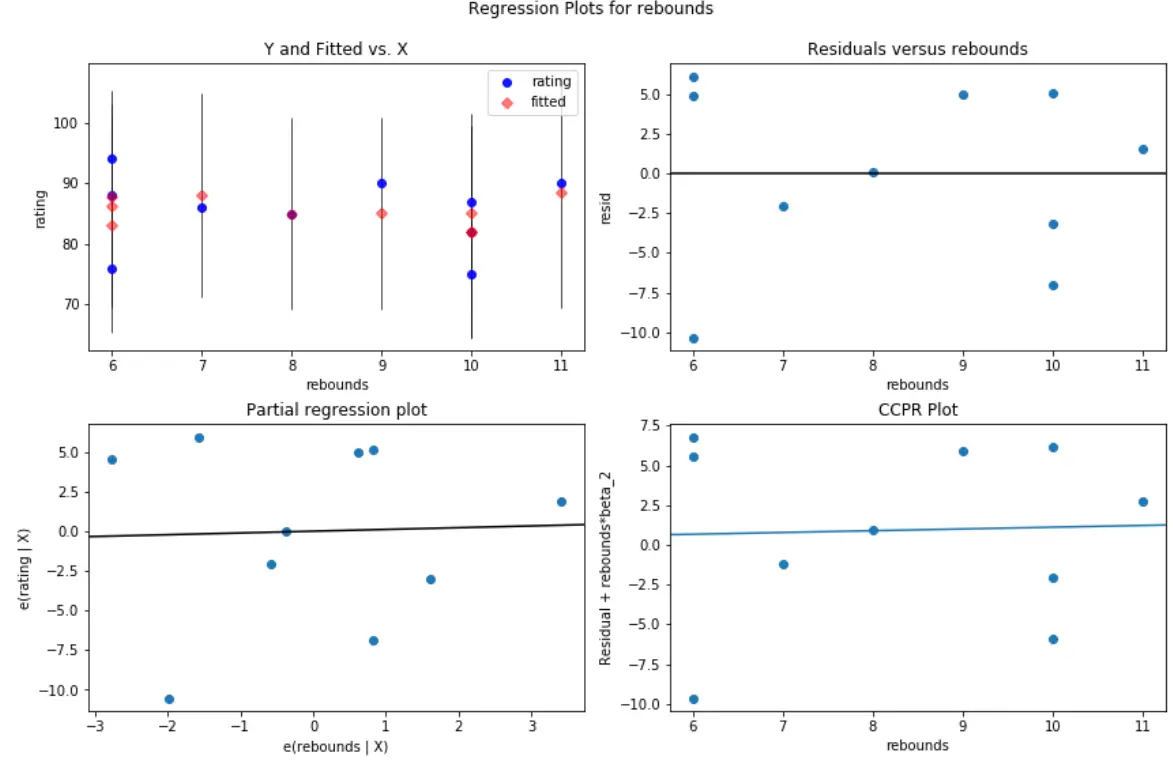
Em ambos os gráficos, os resíduos parecem estar espalhados aleatoriamente em torno de zero, indicando que a heterocedasticidade não é um problema com nenhuma das variáveis preditoras do modelo.