As cinco hipóteses da correlação de pearson

O coeficiente de correlação de Pearson (também conhecido como “coeficiente de correlação produto-momento”) mede a associação linear entre duas variáveis.

Sempre assume um valor entre -1 e 1 onde:

• -1 indica uma correlação linear perfeitamente negativa entre duas variáveis
• 0 indica nenhuma correlação linear entre duas variáveis
• 1 indica uma correlação linear perfeitamente positiva entre duas variáveis

Contudo, antes de calcular o coeficiente de correlação de Pearson entre duas variáveis, devemos garantir que cinco pressupostos sejam atendidos:

1. Nível de medição: Ambas as variáveis devem ser medidas no nível de intervalo ou razão .

2. Relação linear: Deve haver uma relação linear entre as duas variáveis.

3. Normalidade: ambas as variáveis devem ter distribuição aproximadamente normal.

4. Pares relacionados: Cada observação no conjunto de dados deve ter um par de valores.

5. Sem valores discrepantes: Não deve haver valores discrepantes extremos no conjunto de dados.

Neste artigo, fornecemos uma explicação de cada suposição e também como determinar se a suposição foi atendida.

Hipótese 1: Nível de medição

Para calcular um coeficiente de correlação de Pearson entre duas variáveis, ambas as variáveis devem ser medidas no nível de intervalo ou razão .

O gráfico a seguir fornece uma explicação rápida dos quatro níveis em que as variáveis podem ser medidas:

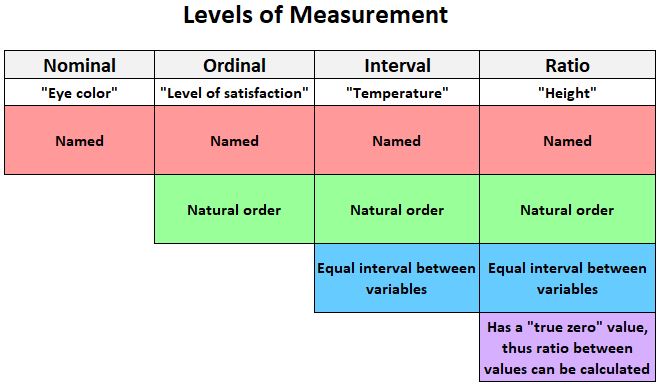
Aqui estão alguns exemplos de variáveis que podem ser medidas em uma escala de intervalo :

• Temperatura: medida em Fahrenheit ou Celsius
• Pontuações de crédito: medidas de 300 a 850
• Pontuações SAT: medidas de 400 a 1.600

Aqui estão alguns exemplos de variáveis que podem ser medidas em uma escala de proporção :

• Altura: medida em centímetros, polegadas, pés, etc.
• Peso: medido em quilogramas, libras, etc.
• Comprimento: Medido em centímetros, polegadas, pés, etc.

Se as variáveis forem medidas em nível ordinal , será necessário calcular o coeficiente de correlação de Spearman entre elas.

Relacionado: Níveis de Medição: Nominal, Ordinal, Intervalo e Razão

Hipótese 2: Relacionamento linear

Para calcular um coeficiente de correlação de Pearson entre duas variáveis, deve haver uma relação linear entre as duas variáveis.

A maneira mais fácil de testar esta hipótese é simplesmente criar um gráfico de dispersão das duas variáveis. Se os pontos no gráfico seguem aproximadamente uma linha reta, então existe uma relação linear:

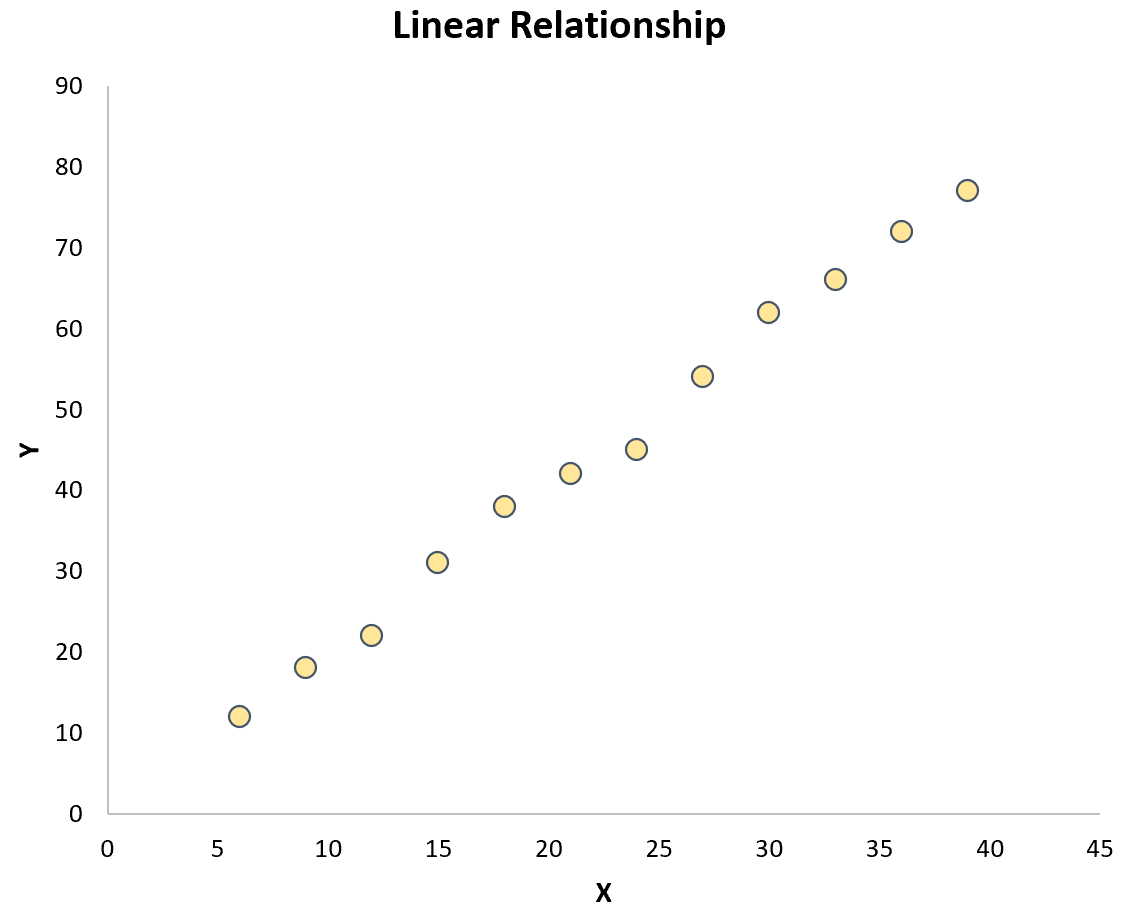
No entanto, se os pontos estiverem espalhados aleatoriamente pelo gráfico ou tiverem algum outro tipo de relacionamento (como quadrático), então não existe um relacionamento linear entre as variáveis:

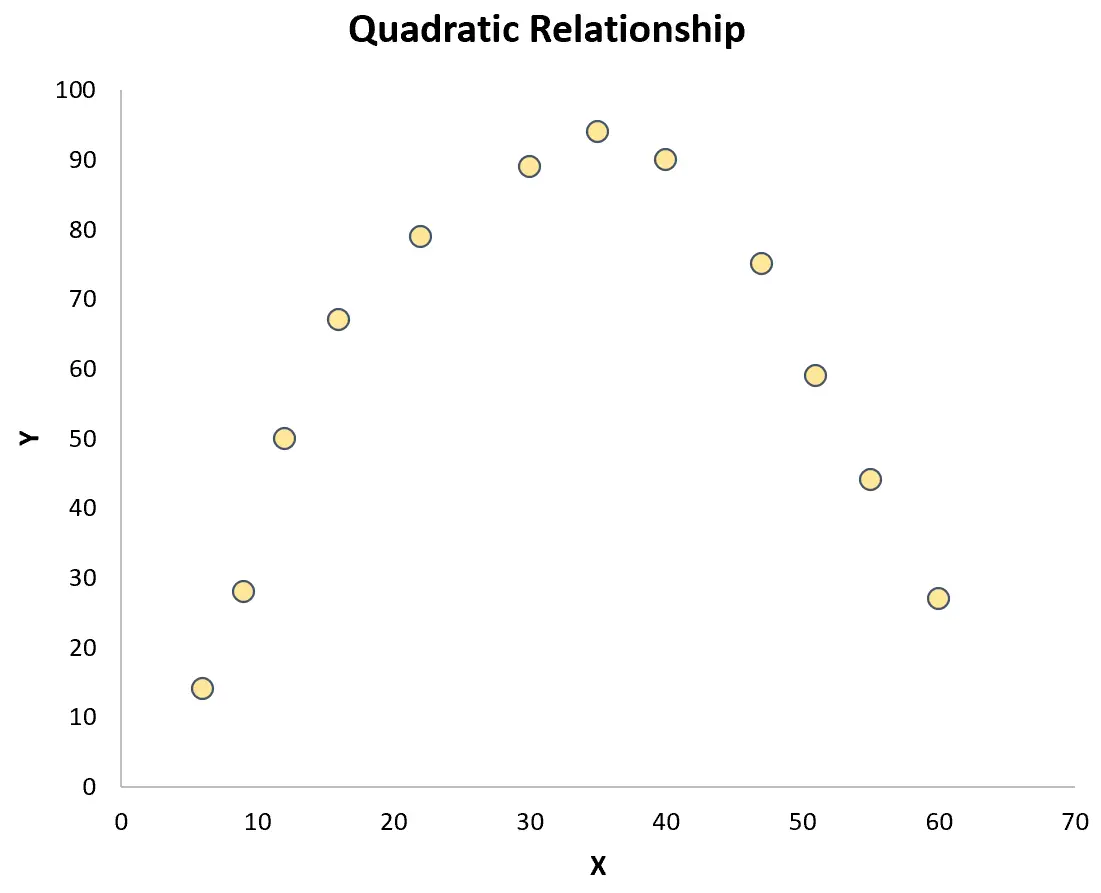
Neste caso, um coeficiente de correlação de Pearson não captará adequadamente a relação entre as variáveis.

Hipótese 3: normalidade

Um coeficiente de correlação de Pearson também assume que as duas variáveis têm distribuição aproximadamente normal .

Você pode verificar essa suposição visualmente criando um histograma ou gráfico QQ para cada variável.

1. Histograma

Se o histograma de um conjunto de dados tiver aproximadamente o formato de um sino, é provável que os dados sejam distribuídos normalmente.

2. QQTerra

Um gráfico QQ, abreviação de “quantil-quantil”, é um tipo de gráfico que exibe quantis teóricos ao longo do eixo x (ou seja, onde seus dados estariam se seguissem uma distribuição normal) e quantis de amostras ao longo do eixo y. (ou seja, onde seus dados realmente residem).

Se os valores dos dados seguirem uma linha aproximadamente reta formando um ângulo de 45 graus, então os dados serão considerados normalmente distribuídos.

Você também pode realizar um teste estatístico formal para determinar se uma variável tem distribuição normal.

Se o valor p do teste estiver abaixo de um certo nível de significância (como α = 0,05), então você tem evidências suficientes para dizer que os dados não são normalmente distribuídos.

Existem três testes estatísticos comumente usados para testar a normalidade:

1. O teste Jarque-Bera

• Como realizar um teste Jarque-Bera no Excel
• Como realizar um teste Jarque-Bera em R
• Como realizar um teste Jarque-Bera em Python

2. O teste de Shapiro-Wilk

• Como realizar um teste de Shapiro-Wilk em R
• Como realizar um teste Shapiro-Wilk em Python

3. O teste Kolmogorov-Smirnov

• Como realizar um teste de Kolmogorov-Smirnov em R
• Como realizar um teste Kolmogorov-Smirnov em Python

Hipótese 4: Pares relacionados

Um coeficiente de correlação de Pearson também assume que cada observação no conjunto de dados deve ter um par de valores.

Esta hipótese é fácil de verificar. Por exemplo, se você estiver calculando a correlação entre peso e altura, basta verificar se cada observação no conjunto de dados possui uma medida de peso e uma medida de altura.

Hipótese 5: Sem valores discrepantes

Um coeficiente de correlação de Pearson também pressupõe que não há valores discrepantes extremos no conjunto de dados, porque os valores discrepantes afetam fortemente o cálculo do coeficiente de correlação.

Para ilustrar isso, considere o seguinte conjunto de dados:

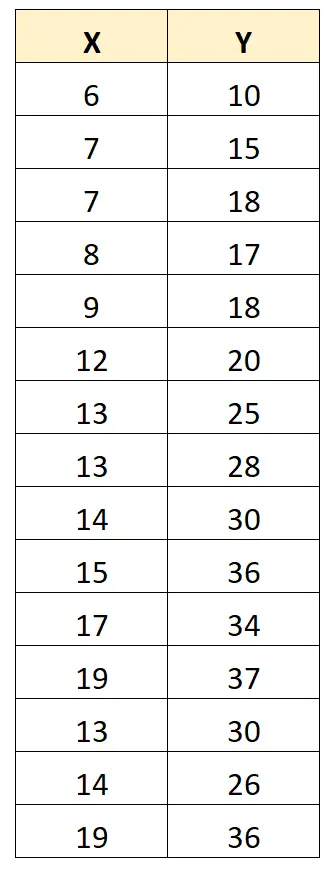
O coeficiente de correlação de Pearson entre X e Y é 0,949 .

No entanto, suponha que tenhamos um valor discrepante no conjunto de dados:

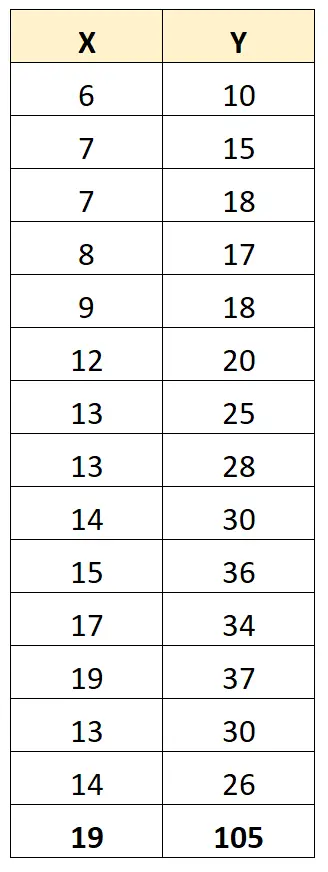
O coeficiente de correlação de Pearson entre X e Y é agora 0,711 .

Um valor discrepante altera significativamente o coeficiente de correlação de Pearson entre as duas variáveis. Nesse caso, pode fazer sentido remover o valor discrepante do conjunto de dados.

Relacionado: O guia completo: quando remover valores discrepantes nos dados

Recursos adicionais

Os tutoriais a seguir fornecem informações adicionais sobre a correlação de Pearson:

Introdução ao Coeficiente de Correlação de Pearson
Como relatar a correlação de Pearson no formato APA
Como calcular manualmente um coeficiente de correlação de Pearson