Como verificar as suposições da anova

Uma ANOVA unidirecional é um teste estatístico usado para determinar se há ou não uma diferença significativa entre as médias de três ou mais grupos independentes.

Aqui está um exemplo de quando podemos usar uma ANOVA unidirecional:

Você divide aleatoriamente uma turma de 90 alunos em três grupos de 30. Cada grupo usa uma técnica de estudo diferente durante um mês para se preparar para um exame. No final do mês, todos os alunos fazem o mesmo exame.

Você quer saber se a técnica de estudo tem ou não impacto nas notas dos exames. Portanto, você realiza uma ANOVA unidirecional para determinar se há uma diferença estatisticamente significativa entre as pontuações médias dos três grupos.

Antes de podermos realizar uma ANOVA unidirecional, devemos primeiro verificar se três suposições foram atendidas.

1. Normalidade – Cada amostra foi retirada de uma população normalmente distribuída.

2. Variâncias iguais – As variâncias das populações das quais as amostras são extraídas são iguais.

3. Independência – As observações dentro de cada grupo são independentes umas das outras e as observações dentro dos grupos foram obtidas por amostragem aleatória.

Se estes pressupostos não forem cumpridos, os resultados da nossa ANOVA unidirecional podem não ser fiáveis.

Neste artigo explicamos como verificar essas suposições e o que fazer se alguma delas for violada.

Suposição nº 1: normalidade

ANOVA assume que cada amostra foi retirada de uma população normalmente distribuída.

Como verificar esta hipótese em R:

Para verificar esta hipótese, podemos usar duas abordagens:

• Verifique visualmente a hipótese usando histogramas ou gráficos QQ .
• Verifique a hipótese usando testes estatísticos formais como Shapiro-Wilk, Kolmogorov-Smironov, Jarque-Barre ou D’Agostino-Pearson.

Por exemplo, suponha que recrutamos 90 pessoas para participar de um experimento de perda de peso no qual designamos aleatoriamente 30 pessoas para seguir o Programa A, o Programa B ou o Programa C durante um mês. Para ver se o programa tem impacto na perda de peso, queremos realizar uma ANOVA unidirecional. O código a seguir demonstra como verificar a suposição de normalidade usando histogramas, gráficos QQ e um teste de Shapiro-Wilk.

1. Ajuste o modelo ANOVA.

 #make this example reproducible
set.seed(0)

#create data frame
data <- data. frame (program = rep(c(" A ", " B ", " C "), each = 30 ),
                   weight_loss = c(runif(30, 0, 3),
                                   runif(30, 0, 5),
                                   runif(30, 1, 7)))

#fit the one-way ANOVA model
model <- aov(weight_loss ~ program, data = data)

2. Crie um histograma dos valores de resposta.

 #create histogram
hist(data$weight_loss)

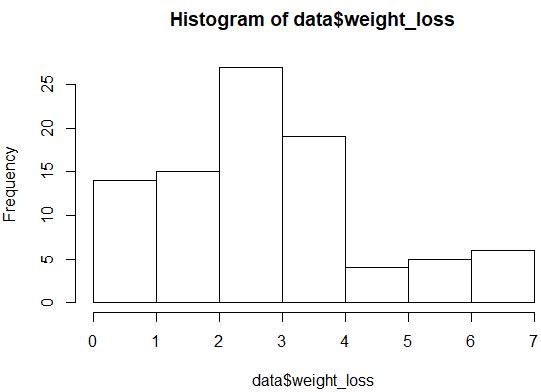
A distribuição não parece distribuída de maneira muito normal (por exemplo, não tem formato de “sino”), mas também podemos criar um gráfico QQ para dar uma outra olhada na distribuição.

3. Crie um gráfico QQ de resíduos

 #create QQ plot to compare this dataset to a theoretical normal distribution
qqnorm(model$residuals)

#add straight diagonal line to plot
qqline(model$residuals) 

Em geral, se os pontos de dados estiverem ao longo de uma linha reta diagonal em um gráfico QQ, então o conjunto de dados provavelmente segue uma distribuição normal. Nesse caso, podemos observar que há um desvio perceptível da linha nas extremidades, o que pode indicar que os dados não estão distribuídos normalmente.

4. Realize o teste de Shapiro-Wilk para verificar a normalidade.

 #Conduct Shapiro-Wilk Test for normality
shapiro. test (data$weight_loss)

#Shapiro-Wilk normality test
#
#data: data$weight_loss
#W = 0.9587, p-value = 0.005999

O teste de Shapiro-Wilk testa a hipótese nula de que as amostras provêm de uma distribuição normal contra a hipótese alternativa de que as amostras não provêm de uma distribuição normal. Nesse caso, o valor p do teste é 0,005999 , que é inferior ao nível alfa de 0,05. Isso sugere que as amostras não seguem uma distribuição normal.

O que fazer se esta suposição não for respeitada:

Em geral, uma ANOVA unidirecional é considerada bastante robusta contra violações da suposição de normalidade, desde que os tamanhos das amostras sejam grandes o suficiente.

Além disso, se você tiver amostras extremamente grandes, testes estatísticos como o teste de Shapiro-Wilk quase sempre dirão que seus dados não são normais. Por esse motivo, geralmente é melhor inspecionar visualmente seus dados usando gráficos como histogramas e gráficos QQ. Apenas olhando os gráficos você pode ter uma boa ideia se os dados estão normalmente distribuídos ou não.

Se a suposição de normalidade for gravemente violada ou se você apenas quiser ser muito conservador, você tem duas opções:

(1) Transforme os valores de resposta dos seus dados para que as distribuições sejam distribuídas de forma mais normal.

(2) Realizar um teste não paramétrico equivalente, como o teste de Kruskal-Wallis , que não requer a suposição de normalidade.

Suposição nº 2: variância igual

ANOVA assume que as variâncias das populações das quais as amostras são extraídas são iguais.

Como verificar esta hipótese em R:

Podemos verificar esta hipótese em R usando duas abordagens:

• Verifique visualmente a hipótese usando boxplots.
• Teste a hipótese usando testes estatísticos formais, como o teste de Bartlett.

O código a seguir demonstra como fazer isso, usando o mesmo conjunto de dados falsos de perda de peso que criamos anteriormente.

1. Crie gráficos de caixa.

 #Create box plots that show distribution of weight loss for each group
boxplot(weight_loss ~ program, xlab=' Program ', ylab=' Weight Loss ', data=data)

A variância na perda de peso em cada grupo pode ser observada pelo comprimento de cada boxplot. Quanto mais longa for a caixa, maior será a variância. Por exemplo, podemos ver que a variância é um pouco maior para os participantes do Programa C em comparação com o Programa A e o Programa B.

2. Realize o teste de Bartlett.

 #Create box plots that show distribution of weight loss for each group
bartlett. test (weight_loss ~ program, data=data)

#Bartlett test of homogeneity of variances
#
#data: weight_loss by program
#Bartlett's K-squared = 8.2713, df = 2, p-value = 0.01599

O teste de Bartlett testa a hipótese nula de que as amostras têm variâncias iguais contra a hipótese alternativa de que as amostras não têm variâncias iguais. Nesse caso, o valor p do teste é 0,01599 , que é inferior ao nível alfa de 0,05. Isto sugere que as amostras não têm todas a mesma variância.

O que fazer se esta suposição não for respeitada:

Em geral, uma ANOVA unidirecional é considerada bastante robusta a violações da suposição de variâncias iguais, desde que cada grupo tenha o mesmo tamanho de amostra.

No entanto, se os tamanhos amostrais não forem iguais e essa suposição for gravemente violada, você poderá executar um teste de Kruskal-Wallis , que é a versão não paramétrica da ANOVA unidirecional.

Suposição nº 3: Independência

ANOVA assume:

• As observações de cada grupo são independentes das observações de todos os outros grupos.
• As observações dentro de cada grupo foram obtidas por uma amostra aleatória.

Como verificar esta hipótese:

Não existe um teste formal que você possa usar para verificar se as observações em cada grupo são independentes e se foram obtidas por uma amostra aleatória. A única maneira de satisfazer esta suposição é usar um desenho aleatório.

O que fazer se esta suposição não for respeitada:

Infelizmente, não há muito que você possa fazer se essa suposição não for atendida. Simplificando, se os dados foram coletados de tal forma que as observações em cada grupo não fossem independentes das observações em outros grupos, ou se as observações dentro de cada grupo não foram obtidas por um processo randomizado, os resultados da ANOVA não serão confiáveis. .

Se esta suposição não for atendida, a melhor coisa a fazer é recriar o experimento usando um desenho aleatório.

Leitura adicional:

Como realizar ANOVA unidirecional em R
Como realizar ANOVA unidirecional no Excel