As cinco suposições da regressão linear múltipla

A regressão linear múltipla é um método estatístico que podemos usar para compreender a relação entre múltiplas variáveis preditoras e uma variável de resposta .

No entanto, antes de realizar a regressão linear múltipla, devemos primeiro garantir que cinco pressupostos sejam atendidos:

1. Relacionamento linear: Existe um relacionamento linear entre cada variável preditora e a variável resposta.

2. Sem multicolinearidade: nenhuma das variáveis preditoras está altamente correlacionada entre si.

3. Independência: As observações são independentes.

4. Homocedasticidade: os resíduos possuem variância constante em cada ponto do modelo linear.

5. Normalidade multivariada: Os resíduos do modelo são normalmente distribuídos.

Se uma ou mais destas suposições não forem cumpridas, então os resultados da regressão linear múltipla podem não ser fiáveis.

Neste artigo, fornecemos uma explicação para cada suposição, como determinar se a suposição foi atendida e o que fazer se a suposição não for atendida.

Hipótese 1: Relacionamento linear

A regressão linear múltipla assume que existe uma relação linear entre cada variável preditora e a variável de resposta.

Como determinar se essa suposição é atendida

A maneira mais simples de determinar se essa suposição é atendida é criar um gráfico de dispersão de cada variável preditora e da variável de resposta.

Isso permite ver visualmente se existe uma relação linear entre as duas variáveis.

Se os pontos no gráfico de dispersão estiverem aproximadamente ao longo de uma linha reta diagonal, é provável que haja uma relação linear entre as variáveis.

Por exemplo, os pontos no gráfico abaixo parecem cair em uma linha reta, indicando que existe uma relação linear entre esta variável preditora específica (x) e a variável de resposta (y):

O que fazer se esta suposição não for respeitada

Se não houver uma relação linear entre uma ou mais variáveis preditoras e a variável resposta, então temos várias opções:

1. Aplique uma transformação não linear à variável preditora, por exemplo, obtendo o log ou a raiz quadrada. Muitas vezes, isso pode tornar o relacionamento mais linear.

2. Adicione outra variável preditora ao modelo. Por exemplo, se o gráfico de x versus y tiver uma forma parabólica, pode fazer sentido adicionar X ² como uma variável preditora adicional no modelo.

3. Remova a variável preditora do modelo. No caso mais extremo, se não existir uma relação linear entre uma determinada variável preditora e a variável resposta, então pode não ser útil incluir a variável preditora no modelo.

Hipótese 2: sem multicolinearidade

A regressão linear múltipla assume que nenhuma das variáveis preditoras está altamente correlacionada entre si.

Quando uma ou mais variáveis preditoras são altamente correlacionadas, o modelo de regressão sofre de multicolinearidade , tornando as estimativas dos coeficientes do modelo não confiáveis.

Como determinar se essa suposição é atendida

A maneira mais simples de determinar se essa suposição é atendida é calcular o valor VIF para cada variável preditora.

Os valores VIF começam em 1 e não têm limite superior. Geralmente, valores VIF acima de 5* indicam potencial multicolinearidade.

Os tutoriais a seguir mostram como calcular o VIF em vários softwares estatísticos:

• Como calcular VIF em R
• Como calcular VIF em Python
• Como calcular VIF no Excel

*Às vezes, os pesquisadores usam um valor VIF de 10, dependendo da área de estudo.

O que fazer se esta suposição não for respeitada

Se uma ou mais variáveis preditoras tiverem um valor VIF maior que 5, a maneira mais fácil de resolver esse problema é simplesmente remover as variáveis preditoras com valores VIF altos.

Como alternativa, se você quiser manter cada variável preditora no modelo, poderá usar um método estatístico diferente, como regressão de crista , regressão laço ou regressão de mínimos quadrados parciais , projetado para lidar com variáveis preditoras altamente correlacionadas.

Hipótese 3: Independência

A regressão linear múltipla assume que cada observação no conjunto de dados é independente.

Como determinar se essa suposição é atendida

A maneira mais simples de determinar se esta suposição é atendida é realizar um teste de Durbin-Watson , que é um teste estatístico formal que nos diz se os resíduos (e, portanto, as observações) apresentam ou não autocorrelação.

O que fazer se esta suposição não for respeitada

Dependendo de como essa suposição é violada, você tem diversas opções:

• Para correlação serial positiva, considere adicionar defasagens da variável dependente e/ou independente ao modelo.
• Para correlação serial negativa, certifique-se de que nenhuma de suas variáveis esteja atrasada demais .
• Para correlação sazonal, considere adicionar dummies sazonais ao modelo.

Hipótese 4: homocedasticidade

A regressão linear múltipla assume que os resíduos têm variância constante em cada ponto do modelo linear. Quando este não é o caso, os resíduos sofrem de heterocedasticidade .

Quando a heterocedasticidade está presente em uma análise de regressão, os resultados do modelo de regressão tornam-se não confiáveis.

Especificamente, a heterocedasticidade aumenta a variância das estimativas dos coeficientes de regressão, mas o modelo de regressão não a leva em conta. Isto torna muito mais provável que um modelo de regressão afirme que um termo do modelo é estatisticamente significativo, quando na realidade não o é.

Como determinar se essa suposição é atendida

A maneira mais fácil de determinar se esta suposição é atendida é criar um gráfico dos resíduos padronizados em relação aos valores previstos.

Depois de ajustar um modelo de regressão a um conjunto de dados, você pode criar um gráfico de dispersão que exibe os valores previstos da variável de resposta no eixo x e os resíduos padronizados do modelo no eixo x. você.

Se os pontos no gráfico de dispersão exibirem uma tendência, então a heterocedasticidade está presente.

O gráfico a seguir mostra um exemplo de modelo de regressão em que a heterocedasticidade não é um problema:

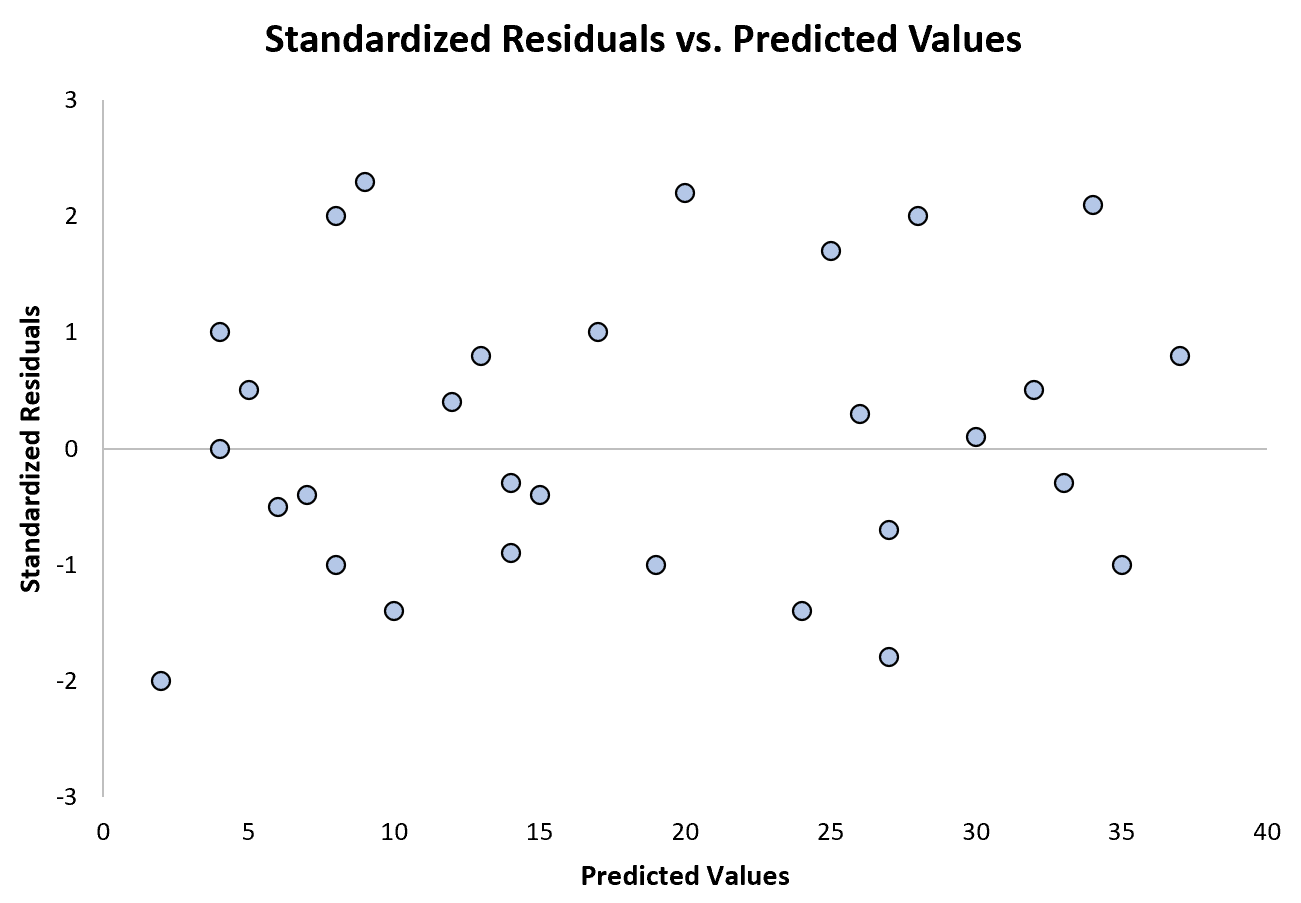
Observe que os resíduos padronizados estão espalhados em torno de zero, sem um padrão claro.

O gráfico a seguir mostra um exemplo de modelo de regressão onde a heterocedasticidade é um problema:

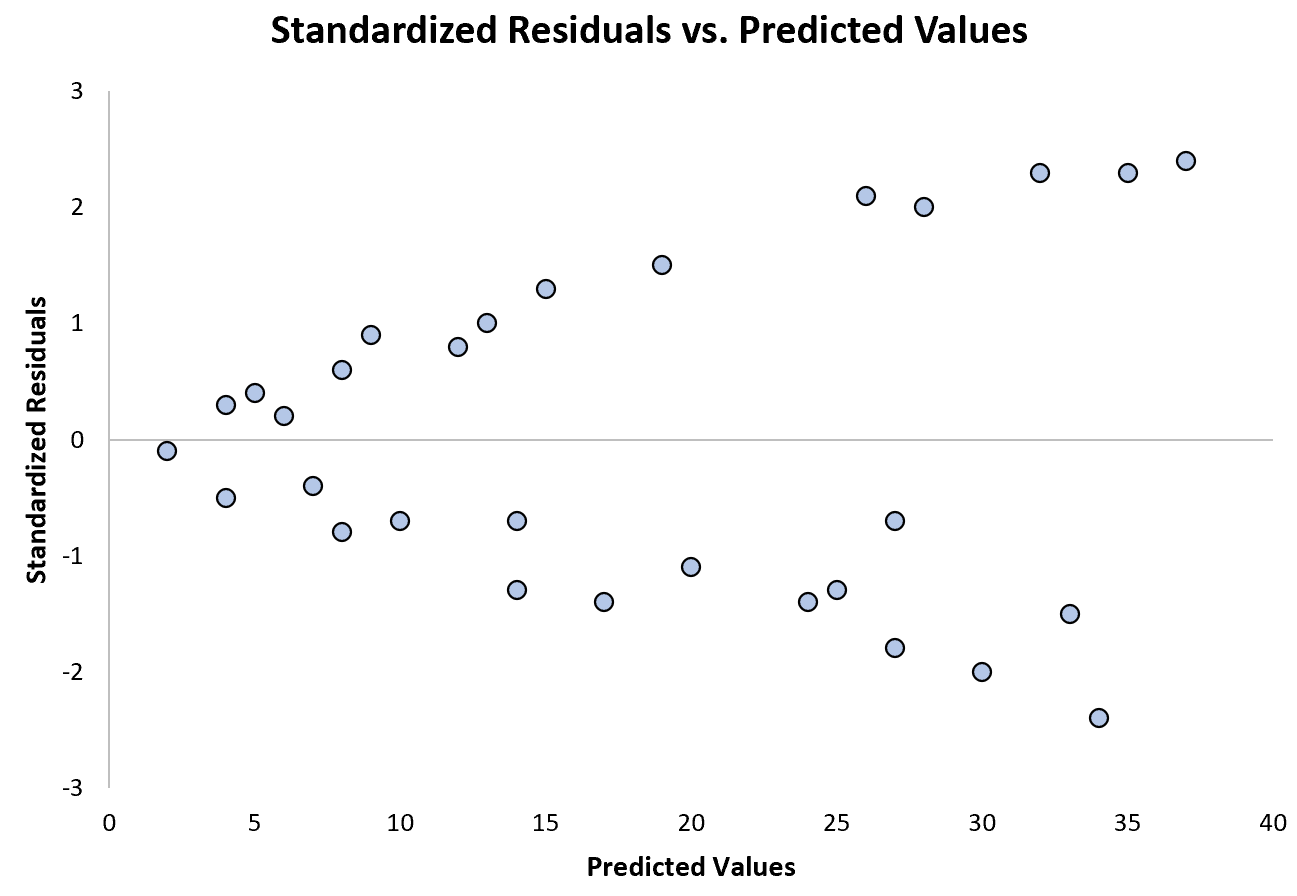
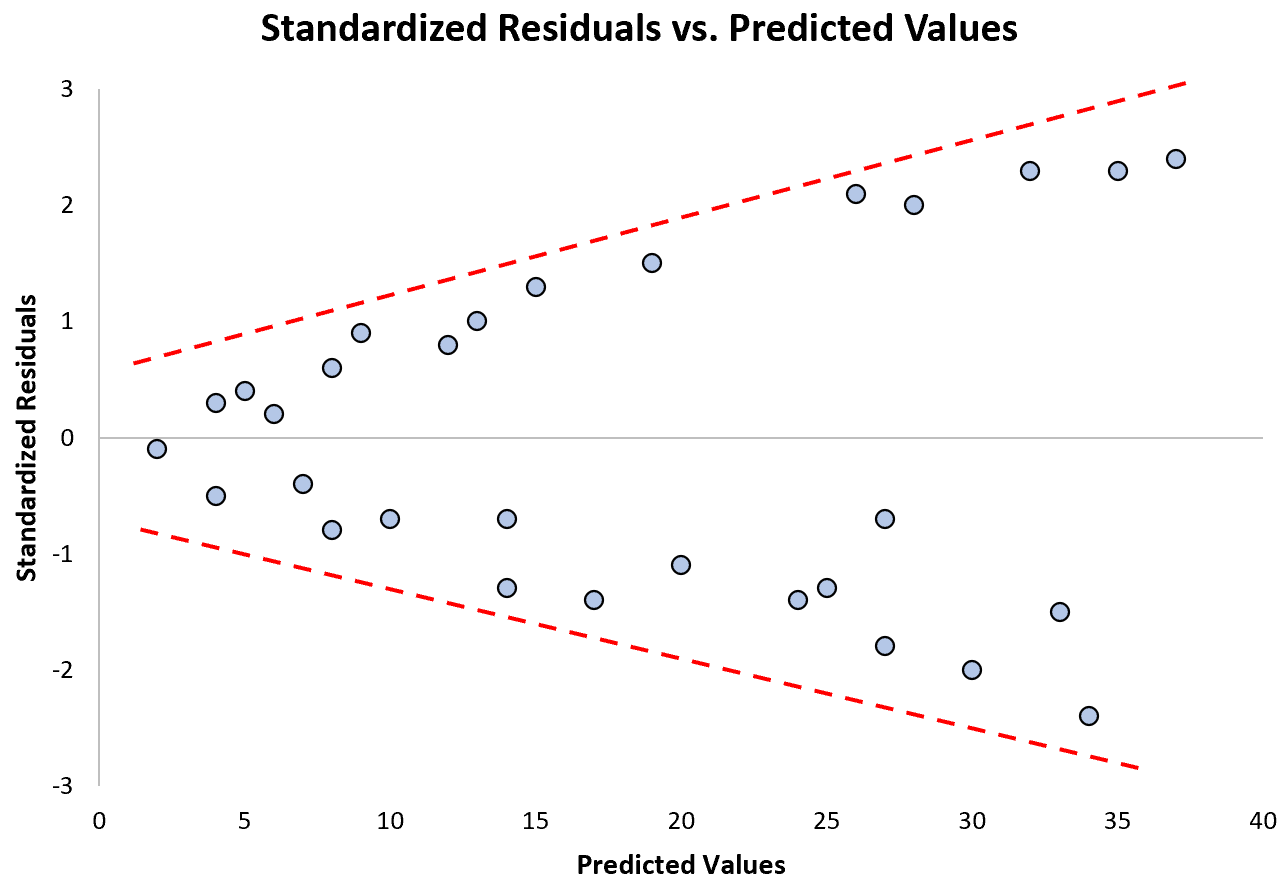
Observe como os resíduos padronizados se espalham cada vez mais à medida que os valores previstos aumentam. Esta forma de “cone” é um sinal clássico de heterocedasticidade:

O que fazer se esta suposição não for respeitada

Existem três maneiras comuns de corrigir a heterocedasticidade:

1. Transforme a variável de resposta. A maneira mais comum de lidar com a heterocedasticidade é transformar a variável de resposta obtendo o log, a raiz quadrada ou a raiz cúbica de todos os valores da variável de resposta. Isso geralmente resulta no desaparecimento da heterocedasticidade.

2. Redefina a variável de resposta. Uma forma de redefinir a variável de resposta é usar uma taxa em vez do valor bruto. Por exemplo, em vez de utilizar o tamanho da população para prever o número de floristas numa cidade, podemos utilizar o tamanho da população para prever o número de floristas per capita.

Na maioria dos casos, isto reduz a variabilidade que ocorre naturalmente em populações maiores, uma vez que estamos a medir o número de floristas por pessoa, em vez do número de floristas em si.

3. Use regressão ponderada. Outra forma de corrigir a heterocedasticidade é usar a regressão ponderada, que atribui um peso a cada ponto de dados com base na variância de seu valor ajustado.

Essencialmente, isso atribui pesos baixos aos pontos de dados que possuem variâncias mais altas, reduzindo seus quadrados residuais. Quando os pesos apropriados são usados, isso pode eliminar o problema da heterocedasticidade.

Relacionado : Como realizar a regressão ponderada em R

Suposição 4: Normalidade multivariada

A regressão linear múltipla assume que os resíduos do modelo são normalmente distribuídos.

Como determinar se essa suposição é atendida

Existem duas maneiras comuns de verificar se essa suposição é satisfeita:

1. Verifique visualmente a hipótese usando gráficos QQ .

Um gráfico QQ, abreviação de gráfico quantil-quantil, é um tipo de gráfico que podemos usar para determinar se os resíduos de um modelo seguem ou não uma distribuição normal. Se os pontos no gráfico formarem aproximadamente uma linha reta diagonal, então a suposição de normalidade é atendida.

O gráfico QQ a seguir mostra um exemplo de resíduos que segue aproximadamente uma distribuição normal:

No entanto, o gráfico QQ abaixo mostra um exemplo de caso em que os resíduos se desviam claramente de uma linha reta diagonal, indicando que não seguem a distribuição normal:

2. Verifique a hipótese utilizando um teste estatístico formal como Shapiro-Wilk, Kolmogorov-Smironov, Jarque-Barre ou D’Agostino-Pearson.

Lembre-se de que esses testes são sensíveis a amostras grandes – ou seja, muitas vezes concluem que os resíduos não são normais quando o tamanho da amostra é extremamente grande. É por isso que muitas vezes é mais fácil usar métodos gráficos como um gráfico QQ para verificar esta hipótese.

O que fazer se esta suposição não for respeitada

Se a suposição de normalidade não for atendida, você terá várias opções:

1. Primeiro, verifique se não há valores discrepantes extremos presentes nos dados que resultem em uma violação da suposição de normalidade.

2. Em seguida, você pode aplicar uma transformação não linear à variável de resposta, por exemplo, obtendo a raiz quadrada, log ou raiz cúbica de todos os valores da variável de resposta. Isso geralmente resulta em uma distribuição mais normal dos resíduos do modelo.

Recursos adicionais

Os tutoriais a seguir fornecem informações adicionais sobre regressão linear múltipla e suas suposições:

Introdução à regressão linear múltipla
Um guia para heterocedasticidade em análise de regressão
Um guia para multicolinearidade e VIF em regressão

Os tutoriais a seguir fornecem exemplos passo a passo sobre como realizar regressão linear múltipla usando diferentes softwares estatísticos:

Como realizar regressão linear múltipla no Excel
Como realizar regressão linear múltipla em R
Como realizar regressão linear múltipla no SPSS
Como realizar regressão linear múltipla no Stata