Por que a média é importante nas estatísticas?

A média de um conjunto de dados representa o valor médio do conjunto de dados. É calculado da seguinte forma:

Média = Σx _i / n

Ouro:

• Σ: Um símbolo que significa “soma”
• x _i : A i ^-ésima observação em um conjunto de dados
• n: o número total de observações no conjunto de dados

Por exemplo, suponha que temos o seguinte conjunto de dados com 11 observações:

Conjunto de dados: 3, 4, 4, 6, 7, 8, 12, 13, 15, 16, 17

A média do conjunto de dados é calculada da seguinte forma:

Média = (3+4+4+6+7+8+12+13+15+16+17) / 11 = 9,54

Nas estatísticas, a média é importante pelos seguintes motivos:

1. A média nos dá uma ideia de onde está o “centro” de um conjunto de dados.

2. Devido à forma como é calculada, a média contém informações de cada observação de um conjunto de dados.

O exemplo a seguir ilustra essas duas razões.

Exemplo: Calcular a média de um conjunto de dados

Digamos que temos um conjunto de dados contendo os preços de venda de 10.000 casas diferentes em uma determinada cidade.

Em vez de olhar milhares de linhas de dados brutos , podemos calcular o valor médio para entender rapidamente o preço médio de venda das casas naquela cidade.

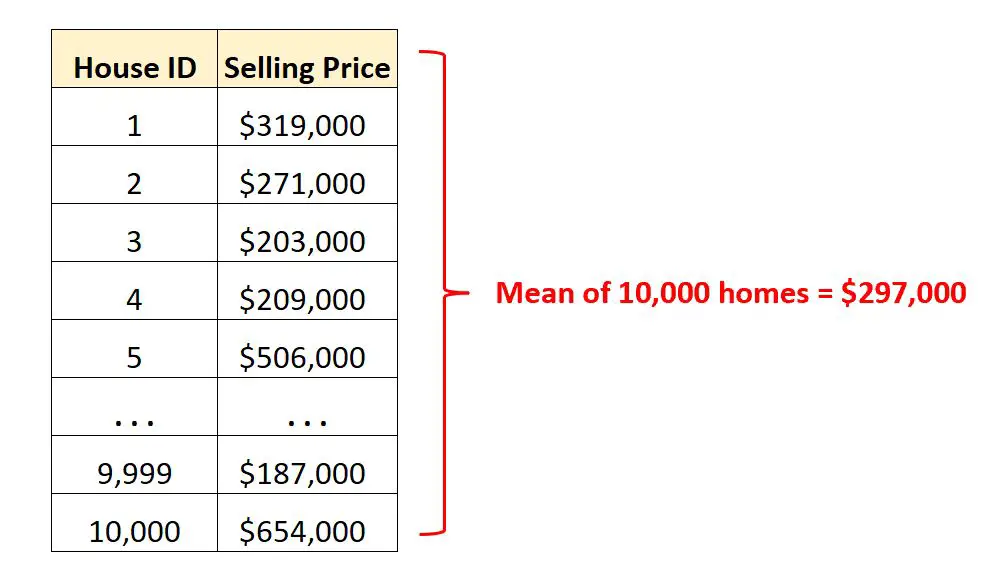
Saber que o preço médio de venda é de US$ 297 mil nos dá uma ideia de quanto custa uma casa “típica” nesta cidade.

Este valor único da média é muito mais fácil de interpretar do que observar todas as linhas de dados brutos.

E como o preço de venda de cada casa foi usado para calcular a média, poderíamos multiplicar o preço médio de venda pelo número total de casas para encontrar o preço total de venda de todas as casas naquela cidade:

• Preço total de venda de todas as casas = Preço médio de venda * Número de casas
• Preço total de venda de todas as casas = $ 297.000 * 10.000
• Preço total de venda de todas as casas = $ 2.970.000.000

Podemos ver que o preço total de venda de todas as casas nesta cidade é de US$ 2,97 bilhões.

Quando usar a média

Ao analisar conjuntos de dados, muitas vezes queremos entender onde está o valor central.

Nas estatísticas, existem duas métricas comuns que usamos para medir o centro de um conjunto de dados:

• Média : o valor médio em um conjunto de dados
• Mediana : o valor mediano em um conjunto de dados

A média é a forma mais comum de medir o centro de um conjunto de dados, mas na verdade pode ser enganosa nas seguintes situações:

• Quando a distribuição é assimétrica .
• Quando a distribuição contémvalores discrepantes .

Para ilustrar isso, considere os dois exemplos a seguir.

Exemplo 1: Calculando a média de uma distribuição distorcida

Considere a seguinte distribuição de salários para residentes de uma determinada cidade:

Os salários elevados no lado direito da distribuição afastam a média do centro da distribuição.

Assim, a mediana reflecte melhor o salário “típico” de um residente do que a média, porque a distribuição é enviesada para a direita.

Neste exemplo específico, o salário médio é de US$ 47.000, enquanto o salário médio é de US$ 32.000.

Assim, a mediana é muito mais representativa do salário típico daquela cidade.

Exemplo 2: Calculando a média na presença de outliers

Considere o seguinte gráfico que mostra a metragem quadrada das casas em uma determinada rua:

A média é fortemente influenciada por algumas casas extremamente grandes, enquanto a mediana não.

Podemos ver que a mediana faz um trabalho melhor ao capturar a metragem quadrada “típica” de uma casa naquela rua do que a média, porque não é influenciada por valores discrepantes.

Resumo

Aqui está um breve resumo das principais conclusões deste artigo:

• A média representa o valor médio em um conjunto de dados.
• A média é importante porque nos dá uma ideia de onde está o valor central em um conjunto de dados.
• A média também é importante porque contém informações de cada observação em um conjunto de dados.
• A média pode ser enganosa quando um conjunto de dados está distorcido ou contém valores discrepantes. Nestes cenários, a mediana dá uma ideia mais precisa de onde está o “centro” de um conjunto de dados.

Recursos adicionais

Os tutoriais a seguir fornecem informações adicionais sobre outras estatísticas descritivas:

Por que a mediana é importante nas estatísticas?
Por que o desvio padrão é importante nas estatísticas?
Quando usar a média versus a mediana