Por que a mediana é importante nas estatísticas?

A mediana representa o valor médio de um conjunto de dados, quando todos os valores são ordenados do menor para o maior.

Por exemplo, a mediana no seguinte conjunto de dados é 19:

Conjunto de dados: 3, 4, 11, 15, 19 , 22, 23, 23, 26

A mediana também representa o percentil ⁵⁰ de um conjunto de dados. Ou seja, exatamente metade dos valores do conjunto de dados estão acima da mediana e metade dos valores estão abaixo.

A mediana é uma métrica importante para calcular porque nos dá uma ideia de onde está o “centro” de um conjunto de dados. Isso também nos dá uma ideia do valor “típico” em um determinado conjunto de dados.

Por exemplo, digamos que temos um conjunto de dados contendo os preços de venda de 10.000 casas diferentes em uma determinada cidade.

Em vez de olhar linhas e mais linhas de dados brutos , podemos calcular o valor mediano para entender rapidamente o preço médio de venda das casas naquela cidade.

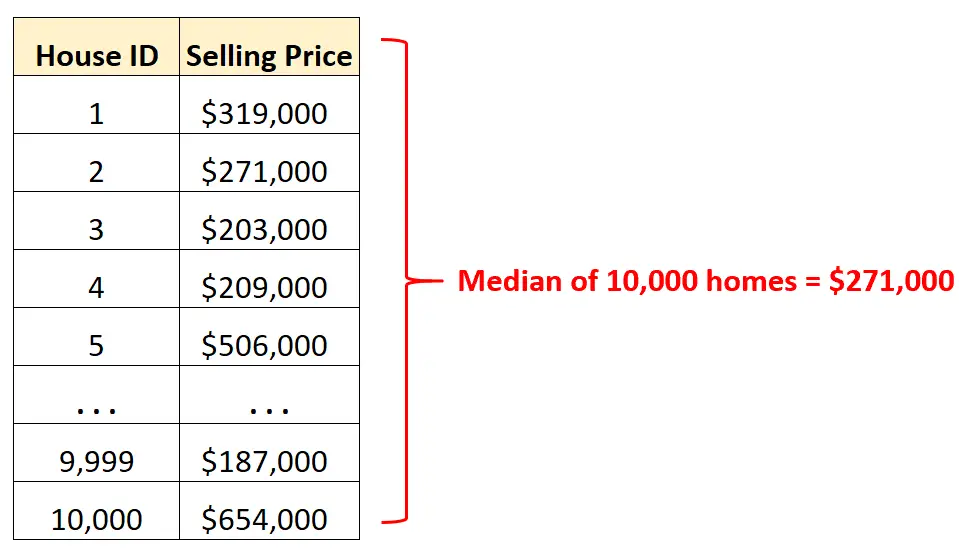
Sabendo que o preço médio de venda é de US$ 271.000, sabemos que exatamente metade das 10.000 casas foram vendidas por mais do que esse valor e a outra metade por menos.

Isto também nos dá uma ideia do preço de venda “típico” das casas nesta cidade.

Quando usar a mediana

Ao analisar conjuntos de dados, muitas vezes queremos entender onde está o valor central.

Nas estatísticas, existem duas métricas comuns que usamos para medir o centro de um conjunto de dados:

• Média : o valor médio em um conjunto de dados
• Mediana : o valor mediano em um conjunto de dados

Acontece que a mediana é uma medida mais útil nas seguintes circunstâncias:

• Quando a distribuição é assimétrica .
• Quando a distribuição contém valores discrepantes.

Para ilustrar isso, considere os dois exemplos a seguir.

Exemplo 1: Calculando a mediana de uma distribuição distorcida

Considere a seguinte distribuição de salários para residentes de uma determinada cidade:

A mediana reflete melhor o salário “típico” de um residente do que a média, porque a distribuição é distorcida para a direita.

Isto significa que os salários elevados no lado direito da distribuição afastam a média do centro da distribuição.

Neste exemplo específico, o salário médio é de US$ 47.000, enquanto o salário médio é de US$ 32.000. A mediana é muito mais representativa do salário típico desta cidade.

Exemplo 2: Cálculo da mediana na presença de outliers

Considere o seguinte gráfico que mostra a metragem quadrada das casas em uma determinada rua:

A média é fortemente influenciada por algumas casas extremamente grandes, enquanto a mediana não.

Podemos ver que a mediana faz um trabalho melhor ao capturar a metragem quadrada “típica” de uma casa naquela rua do que a média, porque não é influenciada por valores discrepantes.

Resumo

Aqui está um breve resumo dos principais pontos abordados neste artigo:

• A mediana representa o valor médio em um conjunto de dados.
• A mediana é importante porque nos dá uma ideia de onde está o valor central em um conjunto de dados.
• A mediana tende a ser mais útil para calcular do que a média quando uma distribuição é distorcida e/ou tem valores discrepantes.

Recursos adicionais

Exemplos concretos: usando média, mediana e moda
Quando usar média vs. Mediana: com exemplos
Por que a moda é importante nas estatísticas?