Como inicializar em r (com exemplos)

Bootstrapping é um método que pode ser usado para estimar o erro padrão de qualquer estatística e produzir um intervalo de confiança para a estatística.

O processo básico para inicialização é o seguinte:

• Pegue k amostras replicadas com substituição de um determinado conjunto de dados.
• Para cada amostra, calcule a estatística de interesse.
• Isso fornece k estimativas diferentes para uma determinada estatística, que você pode usar para calcular o erro padrão da estatística e criar um intervalo de confiança para a estatística.

Podemos inicializar em R usando as seguintes funções da biblioteca de bootstrap :

1. Gere amostras de bootstrap.

inicialização(dados, estatísticas, R,…)

Ouro:

• dados: um vetor, matriz ou bloco de dados
• estatística: uma função que produz a(s) estatística(s) a ser(em) iniciada(s)
• A: Número de repetições de bootstrap

2. Gere um intervalo de confiança de bootstrap.

boot.ci(objeto de inicialização, conf, tipo)

Ouro:

• bootobject: Um objeto retornado pela função boot()
• conf: O intervalo de confiança a ser calculado. O valor padrão é 0,95
• type: Tipo de intervalo de confiança a ser calculado. As opções incluem ‘padrão’, ‘básico’, ‘stud’, ‘perc’, ‘bca’ e ‘all’ – o padrão é ‘all’

Os exemplos a seguir mostram como usar essas funções na prática.

Exemplo 1: inicializar uma única estatística

O código a seguir mostra como calcular o erro padrão para o R-quadrado de um modelo de regressão linear simples:

 set.seed(0)
library (boot)

#define function to calculate R-squared
rsq_function <- function (formula, data, indices) {
  d <- data[indices,] #allows boot to select sample
  fit <- lm(formula, data=d) #fit regression model
  return (summary(fit)$r.square) #return R-squared of model
}
#perform bootstrapping with 2000 replications
reps <- boot(data=mtcars, statistic=rsq_function, R=2000, formula=mpg~disp)

#view results of boostrapping
reps

ORDINARY NONPARAMETRIC BOOTSTRAP


Call:
boot(data = mtcars, statistic = rsq_function, R = 2000, formula = mpg ~ 
    available)


Bootstrap Statistics:
     original bias std. error
t1* 0.7183433 0.002164339 0.06513426

Dos resultados podemos ver:

• O R-quadrado estimado para este modelo de regressão é 0,7183433 .
• O erro padrão para esta estimativa é 0,06513426 .

Também podemos visualizar rapidamente a distribuição das amostras inicializadas:

 plot(reps)

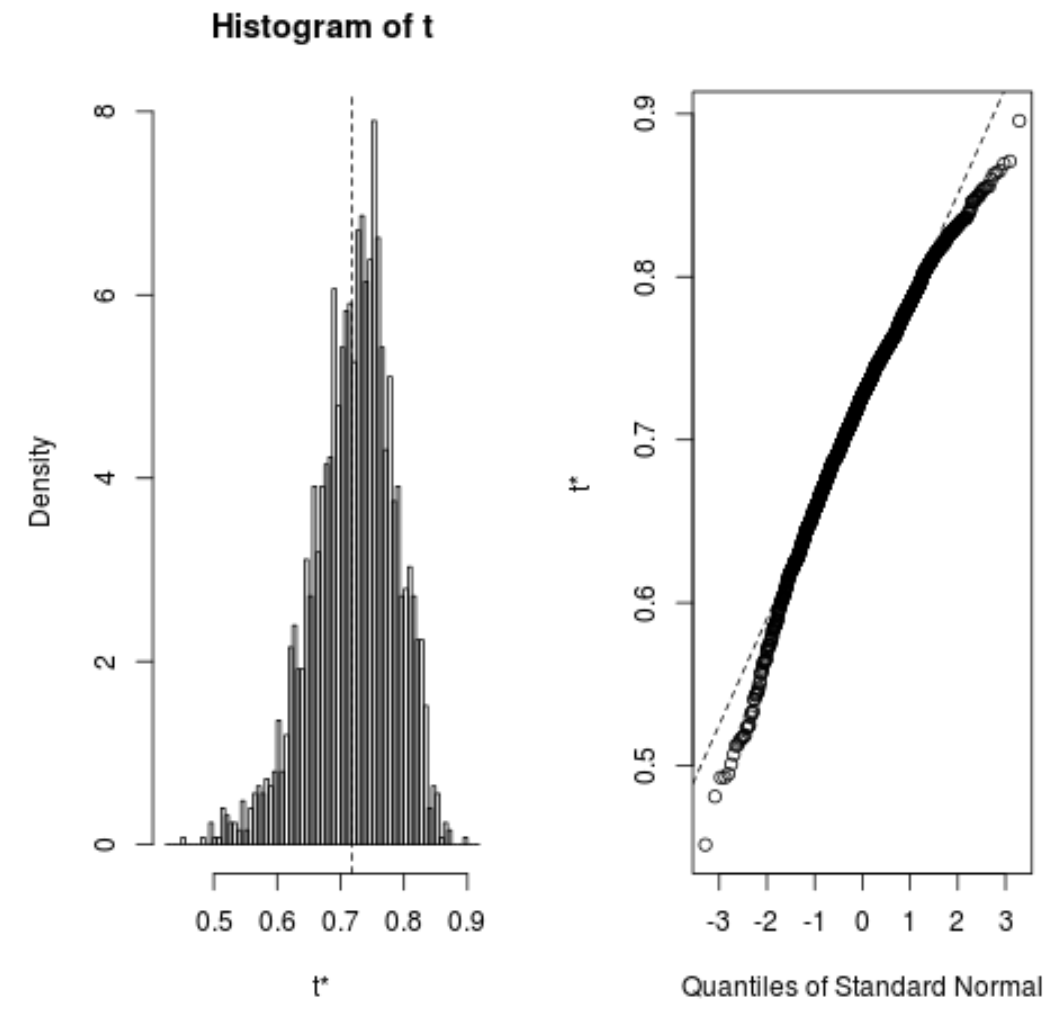
Também podemos usar o código a seguir para calcular o intervalo de confiança de 95% para o R-quadrado estimado do modelo:

 #calculate adjusted bootstrap percentile (BCa) interval
boot.ci(reps, type=" bca ")

CALL: 
boot.ci(boot.out = reps, type = "bca")

Intervals: 
Level BCa          
95% (0.5350, 0.8188)  
Calculations and Intervals on Original Scale

A partir do resultado, podemos ver que o intervalo de confiança de 95% inicializado para os verdadeiros valores de R ao quadrado é (0,5350, 0,8188).

Exemplo 2: inicializar estatísticas múltiplas

O código a seguir mostra como calcular o erro padrão para cada coeficiente em um modelo de regressão linear múltipla:

 set.seed(0)
library (boot)

#define function to calculate fitted regression coefficients
coef_function <- function (formula, data, indices) {
  d <- data[indices,] #allows boot to select sample
  fit <- lm(formula, data=d) #fit regression model
  return (coef(fit)) #return coefficient estimates of model
}

#perform bootstrapping with 2000 replications
reps <- boot(data=mtcars, statistic=coef_function, R=2000, formula=mpg~disp)

#view results of boostrapping
reps

ORDINARY NONPARAMETRIC BOOTSTRAP


Call:
boot(data = mtcars, statistic = coef_function, R = 2000, formula = mpg ~ 
    available)


Bootstrap Statistics:
       original bias std. error
t1* 29.59985476 -5.058601e-02 1.49354577
t2* -0.04121512 6.549384e-05 0.00527082

Dos resultados podemos ver:

• O coeficiente estimado para o intercepto do modelo é 29,59985476 e o erro padrão desta estimativa é 1,49354577 .
• O coeficiente estimado para a variável preditora disp no modelo é -0,04121512 e o erro padrão desta estimativa é 0,00527082 .

Também podemos visualizar rapidamente a distribuição das amostras inicializadas:

 plot(reps, index=1) #intercept of model
plot(reps, index=2) #disp predictor variable

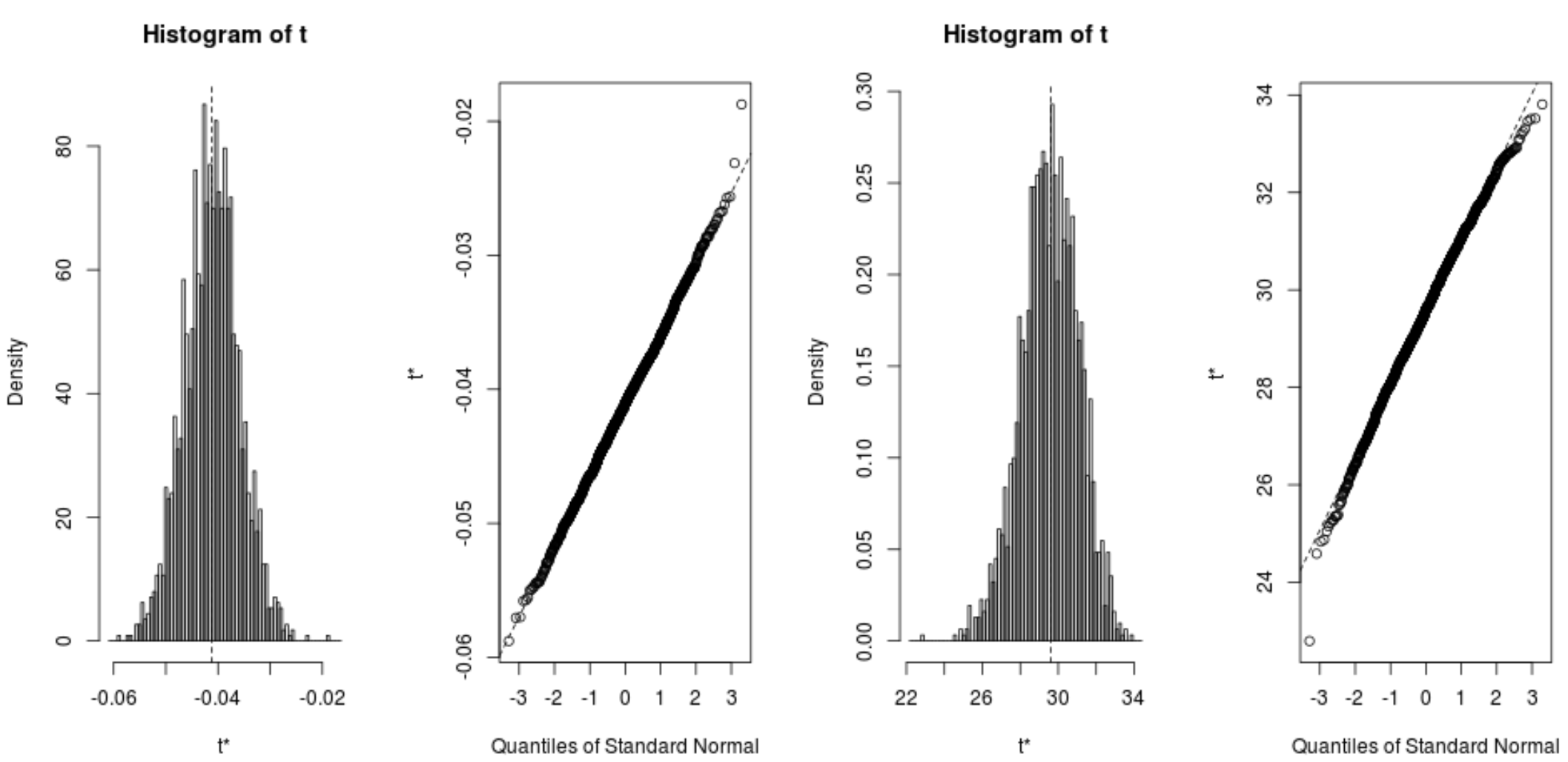
Também podemos usar o seguinte código para calcular os intervalos de confiança de 95% para cada coeficiente:

 #calculate adjusted bootstrap percentile (BCa) intervals
boot.ci(reps, type=" bca ", index=1) #intercept of model
boot.ci(reps, type=" bca ", index=2) #disp predictor variable

CALL: 
boot.ci(boot.out = reps, type = "bca", index = 1)

Intervals: 
Level BCa          
95% (26.78, 32.66)  
Calculations and Intervals on Original Scale
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 2000 bootstrap replicates

CALL: 
boot.ci(boot.out = reps, type = "bca", index = 2)

Intervals: 
Level BCa          
95% (-0.0520, -0.0312)  
Calculations and Intervals on Original Scale

A partir dos resultados, podemos ver que os intervalos de confiança de 95% inicializados para os coeficientes do modelo são os seguintes:

• IC para interceptação: (26,78, 32,66)
• CI para disp : (-0,0520, -0,0312)

Recursos adicionais

Como realizar regressão linear simples em R
Como realizar regressão linear múltipla em R
Introdução aos intervalos de confiança